Class Notes Physics I, 11/11/98
Stable and Unstable Equilibrium; Rotational KE
http://youtu.be/hGcjVtaKXoM
http://youtu.be/8B68glSqcNA
If we consider a cylindrical object, such as a piece of iron bar, resting on a level
service, we see that the weight of the object, acting from its center of mass, is directed
toward the center of the base of the object. This force exerts no rotational influence on
the object.
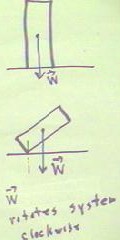
If, however, the object is tilted, the action of the weight vector does exert a
rotational influence about the point on the base of the object which is in contact with
the level service.
- In the second figure below, it
should be clear that the weight of the object will tend to rotate it in a clockwise
direction around its point of contact with the service.
- The object will therefore tend to
rotate in the clockwise direction whenever the line of action of the weight vector falls
outside the point of contact.
- The result of this torque will be
to cause the object to rotate further and further from its equilibrium position, and hence
the fall.
- If the line of action falls inside
the point of contact, the rotation will be in the counterclockwise direction, and the
object will tend to return to its equilibrium position.
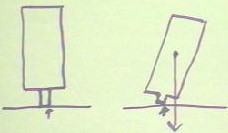
If we compare this situation with the object shown below, we see that compared to the
previous object it takes a much smaller rotation to result in the clockwise torque
necessary to make the object fall. That is, we don't have to rotate the object very
far it all in order for the line of action of its weight to file outside the point
contact.
http://youtu.be/EByHI1_ZFlA
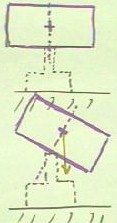
The figures below show an end of view of the wooden beam balancing on the top of the
Mr. Sketch marker.
- The axis of symmetry of the beam is marked with a purple dotted line, which is aligned
with a central axis of the marker.
The center of mass will be at the central point of the beam, assuming a uniform
distribution of mass throughout the beam, and is indicated by the + at this point.
In the second figure below, the beam has been tilted and the line of action of its
weight force has moved past the point contact.
- The beam will therefore tend to
rotate in the clockwise direction and thus to topple.
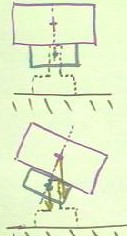
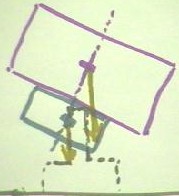
In the second figure below, we depict the same situation, but with a pack of washers
attached below the beam.
- As the beam rotates to the right,
we can see that its center of mass moves to the right and in the picture moves slightly
outside of the point contact.
- The torque of the beam will then
tend to rotate the system clockwise.
- The washers, however, move in the
opposite direction, with their center of mass moving to the left and tending to rotate the
system counterclockwise about the point of contact.
- The center of mass of the beam
itself (not including the washers) will therefore have to move significantly past the
point of contact before the beam can topple, in contrast to the situation before the
washers were attached, when any displacement of the center of mass beyond the point
contact would cause disaster.
A closer look at this system shows how the two forces provide opposing rotational
influences.
http://youtu.be/8es1CPqBLmI
http://youtu.be/Zuz33vDD3gY
When we allowed the washers over the edge of the table to accelerate the beam, we
measured the change in altitude of the washers.
- From this change in altitude we can calculate the change in the potential energy of the
washers.
By making time and angular position measurements on the beam, we were able to determine
the angular velocity attained by the beam.
Using your measurements of the mass of the beam, and the angular velocity attained by
the beam, assume that the beam consists of 8 equal pieces and determine the approximate
resulting kinetic energy of each piece. Compare with the potential energy loss of the
washers.

http://youtu.be/vGSO5623Znc
"
