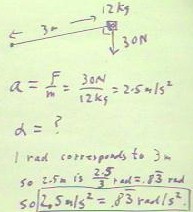"
Class Notes Physics I, 11/13/98
Moment of Inertia
The quiz problem concerned a 12 kg mass under the influence of a 30 Newton force. The
mass was constrained by a thin massless rod to move in a circle of radius 3 meters; the 30
Newton force was to be directed always perpendicular to the rod, at the position of the
force.
We were to find the acceleration of a mass in meters/second/second and its angular
acceleration, in radians/second/second.
- The acceleration is clearly 30 N / 12 kg = 2.5 m/s/s.
From this we can easily find the angular acceleration.
- Recall that a radian is the angle such that the arc distance on a circle corresponding
to this angle is equal to the radius of the circle.
- In the present case the radius of the circle on which the object moves is clearly 3
meters, the length of the constraining rod.
- So a radian on this circle corresponds to an arc distance of 3 meters.
- Two radians would correspond to an arc distance of 2 * 3 m = 6 m; half a radian would
correspond to an arc distance of (1/2) * 3 m = 1.5 m.
- We see in terms of the definition of the
radian that 2.5 meters would correspond to 2.5 / 3 radians or to .833...
radians.
- It follows that the 2.5 m/second/second acceleration
corresponds to an angular acceleration of .833... radians/second/second.
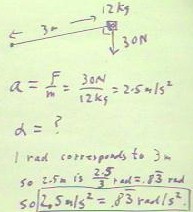
Proceeding a bit more formally:
- An arc distance `ds on a circle of radius r corresponds to an angular displacement
`d`theta such that `ds = r `d`theta
- thus, for example, an angular displacement of one radian does indeed correspond to an
arc distance equal to the radius; be sure you understand why the given relationship is the
only one consistent with the definition of the radian.
- This relationship is shown in the figure below.
- Now if we have an object moving with an average velocity vAve over a time interval `dt,
we see that its displacement `ds along the arc must be such that vAve = `ds / `dt.
- Since `ds = r `d`theta, we see that
- vAve = `ds / `dt = r `d`theta / `dt = r *
(`d`theta / `dt).
- Since `d`theta / `dt is just the average angular velocity (in standard units, the number
of radians per second at which angular position changes), using `omega for angular
velocity to distinguish it from linear velocity, we have
- A similar line of reasoning (starting with aAve = `dv / `dt) shows that average
acceleration is equal to the product of the radius r and the average angular acceleration:
- Now in the present problem, we can see that `alphaAve = a / r = 2.5 m/s^2 / 3 m =
.833... radians/second/second, as we found before.
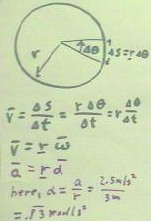
http://youtu.be/mgev7TzaVbQ
http://youtu.be/M9D0w98K8Ns
http://youtu.be/4P8e6AQFdOY
We generalize the problem as in the picture below.
- A mass m subject to a force F, and constrained to rotate in a circle about a fixed point
at radius r and with F perpendicular to the light constraining rod, will have acceleration
a = F / m.
Its angular acceleration will then be be
- `alpha = a / r = F / (mr).
We next consider what happens if the force F is applied not at the position of the
mass, but at a distance x from the axis of rotation, in a direction perpendicular to the
constraining rod.
- Experience shows that if this force is applied at a point closer to the axis of rotation
than the radius, it will have less effect than if applied at the radius.
We might postulate that this force would be equivalent to a proportionally reduced force
acting at the position of the mass.
The proportion would be just the proportion x / r of the distances, so that the
equivalent force exerted at the position of the mass would be F ( x / r ).
Experiment validates this assumption.
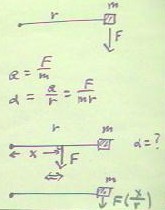
The effect of this force F at distance x from the axis of rotation is seen to be
equivalent to force F (x/r) applied at the position of a mass.
- This force will thus accelerate the mass at the rate
- a = F (x/r) / m = F x / (m r),
- and the angular acceleration will be
- `alpha = a / r = F x / (m r^2).
We see that acceleration is the result of something involving force, compared with
something involving mass. If we compare
- `alpha = F x / (m r^2) with the standard form a = F / m
of Newton's Second Law
we see that F x is analogous to F, while m r^2 is analogous to m.
- The product F x is what accelerates the system, and m r^2 is a property of the system
that resists acceleration.
We call F x the torque of the force F, and we designate this quantity by the Greek
letter `tau
- We call m r^2 the moment of inertia of the force, designated I:
- moment of inertia: I = m r^2.
- Using these symbols we have
This relationship is merely a restatement of Newton's Second Law.
- In the original form of Newton's Second Law it is
the force F that accelerates the system and just the mass m their resists acceleration.
- In its rotational form it is the torque `tau that
accelerates the system and the moment of inertia m r^2 that resists acceleration.
- Newton's Second Law in its first form gives us
acceleration in meters/second/second, while in its second form we get
acceleration in the angular units radians/second/second.

http://youtu.be/1rnFGPAOUTw
We now determine the moment of inertia of a Styrofoam disk in which are embedded 12
bolts, with the disk constrained to rotate about its center.
- Each bolt has mass 18 grams.
Four of the bolts are located at positions 9.5 cm from the center of the disk, four more
are located 6.6 cm from the center, and remaining four at 4.9 cm from the center.
- We see that the moment of inertia of a bolt at 9.5 cm from the center is mr^2 = .00016
kg m^2 (approximately).
- Similar calculations show us that a bolt 6.6 cm
from the center will have approximate moment of inertia .00007 kg m^2, while a bolt 4.4 cm
from the center has moment of inertia .00004 kg m^2.

The total moment of inertia of the bolts will thus be the total for four bolts, each
with moment of inertia .00016 kg m^2, another four bolts each with moment of inertia
.00007 kg m^2, and another four bolts each with moment of inertia .00004 kg m^2.
- The total moment of inertia of the bolts is
therefore .0011 kg m^2.
- The moment of inertia of the styrofoam is
relatively small, and will be neglected for the present calculation.
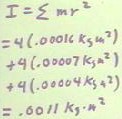
http://youtu.be/SbRuoEm172M
We next hang paper clips from the rim of the disk
by a thread which is wrapped around the rim of the disk.
- We continue to add paper clips until the disk,
given an initial velocity, will continue to rotate at that constant velocity as the paper
clips descend.
- The torque exerted by these paper clips is
therefore seen to balance the friction in the system.
- We then add a 3-gram mass to the clips, so that we
have a net torque equal to that exerted by the 3-gram mass.
Measuring the radius of the disk we find that the force exerted by gravity on the
3-gram mass is applied at a distance of 10.5 cm from the axis of rotation.
- We thus have a net force F = (.003 kg) * 9.8 m/s^2 = .0294 Newtons, acting perpendicular
to the radial line at a distance of .105 cm.
The corresponding net torque of the system is therefore `tauNet = .0294 N * .105
m = .003 m N (approximately).
Recalling that the moment of inertia of the system is approximately .0011 kg m^2, we
see that this net torque should then accelerate the system at the rate
- `alpha = `tau / I = .003 m N / .0011 kg
m^2 = 3 rad/sec^2 (the figure below shows the details of the units calculation).
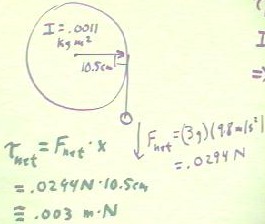
The figure below depicts the calculation of the torque for the above situation.
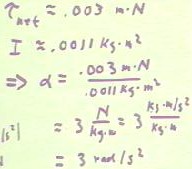
http://youtu.be/Oig409u0Dus
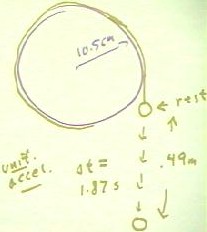
The figure below shows the
situation when the weight hanging from the rim of the wheel is released.
- Starting from rest, the weight descends a distance of .49 meters in 1.87 seconds.
If we assume uniform acceleration, we can calculate the acceleration of the mass and
therefore the acceleration of a point on the rim of wheel (note that the point of
attachment of the thread to the rim of the wheel moves always at the same velocity as the
mass, since we assume that the thread doesn't stretch significantly).
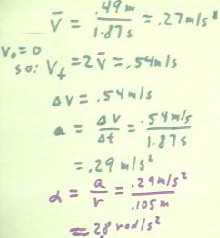
Analyzing the motion of the weight in the usual manner, we determine that its
acceleration is approximately .29 meters/second/second.
- From this acceleration and the radius of the circle we see that the angular acceleration
of wheel must therefore be 2.8 rad/second/second.
- This result compares extremely well with our prediction, based on our calculation of the
moment of inertia and the torque, that the angular acceleration of wheel should be
approximately 3 radians/second/second.
We therefore regard this result as confirmation of the relationship `alpha = `tau / I.
http://youtu.be/QiUP5YAFFHg
"