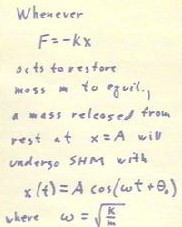
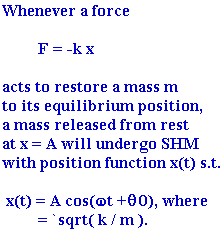
Test Version 8
Show all work and document your analysis.
You will be given a grade for problems 1-8. Each additional problem will be counted if and only if it increases your score.
1. A 200 gram ball rolls down an incline and collides with a second ball of unknown mass. Immediately after collision, and without losing any speed, the two balls leave the ramp traveling initially in the horizontal direction, and fall freely a distance of 80 cm to the floor. From the positions at which the balls strike the floor, it is determined that the first ball has an after-collision velocity of 50 cm / s in direction 345 deg, and the second an after-collision velocity of 80 cm / s in direction 30 deg. Determine the mass of the second ball and the original speed of the first. All angles are measured with respect to the original direction of motion of the first ball.
2. A uniform beam 2 meters long and having a mass of 12 kg is constrained to rotate in a vertical plane about a horizontal axis through one end. When the beam is angled at 30 degrees above horizontal, a vertical string attached to its free end holds it in equilibrium. What must be the tension in the string? What forces will be acting on the axle?
3. On an incline of 20 degrees, a downward vertical force of 50 Newtons is applied to a 30 kg mass. If the coefficient of friction on the incline is .15, that what is the net force on the object?
4. A wheel is formed from a 4 kg hoop of diameter .8 meters, and eight uniform spokes each of mass 8 kg. If a retarding force of 25 N is applied to the hoop, in a direction attention to the circular rim, then how long will it take this force to bring the wheel to a stop from an initial angular velocity of 10 rpm?
5. A projectile is given an initial velocity of 50 meters/second in a direction making an angle of 60 degrees with horizontal, and at an altitude of 17 meters. How far does the projectile travel in the horizontal direction, and what is its speed when it hits the ground?
6. What would be the escape velocity of a rocket from the surface of a spherical asteroid whose radius is 300 km and whose mass is 10^21 kg? How much would you weigh on the surface of this asteroid? What would be your orbital velocity around this asteroid?
7. An 80 kg man wishes to climb a distance of 20 m up a rope, starting from rest and climbing as quickly as possible. The rope, however, is able to exert a maximum tension of 1,000 Newtons without breaking. What is the maximum possible acceleration of the man as he climbs the rope, and how long will it take him to get to the top?
8. A beam accelerates at a rate of 1.2 rad / sec^2, starting from rest and moving from angular position `theta1 = .4 rad to `theta2 = 4.3 rad. What velocity did it attain?
9. Suppose you were climbing a very tall tower, anchored firmly to the planet Earth and rotating along with planet. At what distance from the center of the Earth would you become effectively weightless as a result of your velocity matching the velocity required to orbit at that distance? What would happen to you if you climbed a little higher and let go?
10. From the fact that the total gravitational flux of mass m1 is 4 `pi G m1 and the flux picture, prove Newton's Law of Universal Gravitation F = G m1 m2 / r^2 by first determining the gravitational field strength at distance r from m1, then by determining the force felt by m2 at this distance.
11. What force must be added to a 35 Newton force directed at angle 230 degrees in order to obtain a 70 Newton force directed at angle 160 degrees?
12. The energy required to increase the angular velocity of a beam 5 meters long and with a mass of 50 kg must come from a washer that exerts a torque on the system as it descends. Assuming no dissipative forces, how far must a 10 kg mass descend in order to accelerate the beam, initially at rest, to an angular velocity of one revolution per second?
(Notes to be expanded later)
Review of the basic ideas of SHM:
Example done in class: 2 kg from a spring gave meter stick reading 30.4 cm; 3 kg gave 33.6 cm. `dx = 3.2 cm resulted from added 9.8 N force of gravity due to added 1 kg mass. k = ... = 3.6 * 10^-2 N / m.
Knowing mass = 3 kg, can find `omega = `sqrt( k / m). From `omega we can find period T (time around ref. circle at ang. vel. `omega).
Practice Test Problem 12 (rated most difficult): Find moment of inertia of beam and angular KE change from ang. vel. 0 to 1 rad / s [note: problem said 1 rev / sec; this would be 2 `pi rad / sec, and would modify results obtained below].
This KE change must come from PE decrease m g `dh of 10-kg mass.
Problem 11 (rated next most difficult): Just like problem on introductory set. Add V to F to get R. What is V? Obviously, if F + V = R, V = R - F. Find by components.
From components get magnitude and angle.
Problem # 4 (rated next most difficult): The thing is gonna rotate, so find its moment of inertia. Hoop moment of inertia is just M R^2, since all mass at dist. R from center. Each spoke is effectively a rod rotating about its end, so its moment is 1/3 M L^2; there are 8 spokes.
We're going to slow it down with a force. Find the torque of a 25 N force at .4 m from center of rotation.
Use torque and moment of inertia to get angular accel. We know init. and final vel. The rest is simple.
Problem number 7 (next most difficult): Assume max possible upward force: 1000 N. Only other force is weight, 784 N. Net force is 216 N upward.
So accel. is about 2.7 m/s^2. We know `ds and v0. The rest is straightforward.
"