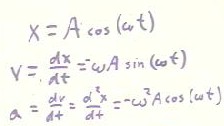
As we have seen, for any simple harmonic oscillator a possible position function is x(t) = A cos(`omega * t). Using calculus we find that the corresponding velocity and acceleration functions are v(t) = -`omega A sin(`omega * t) and a(t) = -`omega^2 A cos(`omega * t). We can use these functions to answer various questions about the position, velocity and acceleration of a simple harmonic oscillator.
The velocity of a pendulum can be represented by v(t) = -`omega A sin(`omega * t), with `omega = `sqrt( k / m) = `sqrt ( g / L ) (for a pendulum k = m g / L). We can with good results test this velocity function by allowing a washer to ride lightly on top of the pendulum; when the pendulum is suddenly stopped the washer continues with nearly unchanged velocity, which we can measure from its range as a projectile.
The reference circle model gives us the same result. At maximum velocity the oscillator is moving at the same speed as the point on the reference circle, which is `omega * A; this coincides with the maximum possible magnitude of the velocity function v(t) = `omega A sin(`omega * t), which occurs when sin(`omega * t) = +- 1. At any other position the vector velocity of the reference point, which velocity is tangent to the circle, will have a horizontal component equal to v(t) = `omega A sin(`omega * t).
Using the circular model we see that the vector acceleration of the point on the reference circle, which is directed radially inward or the center of the circle, has an x component equal to the acceleration a(t) = -`omega^2 * A cos(`omega * t).
Since the work required to move a simple harmonic oscillator from its equilibrium position x = 0 to position x is .5 k x^2 (ave. force .5 k x, distance x), conservation of energy dictates that the kinetic energy at position x is the difference between the maximum potential energy .5 k x^2 at this point in the maximum potential energy .5 k A^2, which is the total energy of the oscillator. From energy considerations we therefore easily derive an expression for the velocity of the oscillator at position x. This function tells us that the velocity of position x can be determine from the proportion x / A recording to v(x) = vMax `sqrt( 1 - (x/A)^2). This prediction is easily validated by an experiment similar to that described above.
We will use the formulas for the position, velocity and acceleration of a simple harmonic oscillator as functions of time to understand the maximum velocity and acceleration of the oscillator.
As we have seen, the SHM (Simple Harmonic Motion) of a pendulum can be modeled by the function x(t) = A cos(`omega t).
- Calculus-literate students will see that x(t) = A sin(`omega t) could be a solution, as could any combination x(t) = A sin (`omega t) + B cos (`omega t), or x(t) = A sin ( `omega t + `theta0) .
- (Calculus-literate students should at this point take the derivative of this function, and the derivative of the resulting function, and think about what these derivatives mean).
If x = A cos(`omega t), it follows that the velocity and acceleration functions will be v = dx / dt = - `omega A sin(`omega t) and a = dv / dt = d^2 x / dt^2 = - `omega^2 A cos(`omega t).
Now, for a pendulum of length L we have `omega = `sqrt(g / L), which you will recall is a specific case of the general `omega = `sqrt(k / m) with k equal to the factor k = m g / L (obtained from the horizontal tension) .
We now find the maximum velocity implied by the velocity function v(t) = - `omega A sin(`omega t).
If we release our 1.5 meter pendulum from rest at a position 30 cm from its equilibrium position, we will have A = 30 cm and `omega = 2.6 rad/s.
Now if we have `omega = 2.6 rad/s and A = 30 cm, it follows that the maximum velocity of the pendulum is vMax = `omega A = 78 cm/s.
We can easily test this result.
In the situation observed in class the vertical displacement of the falling washer was -1.16 meter, which as shown below requires a time of .49 sec for the fall.
Using an eyeball estimate of the range along a meter stick, we observed a horizontal range of approximately 37 cm, which implies a horizontal velocity of approximately 75 cm/second.
At any position on the reference circle, the velocity of the pendulum will be the horizontal component of the 78 cm/sec velocity vector.
At any position between the extreme right and left and extreme top and bottom positions on the reference circle the velocity of the reference point will have horizontal and vertical components that both have magnitudes less than 78 cm/s.
When the reference point is at the top or the bottom of the circle, it is clear that this point is moving parallel to the pendulum and that the velocity of the vertical projection of this point is therefore equal to the velocity of the reference point.
In general we will note that the maximum velocity of a simple harmonic oscillator model by a reference circle of radius A with the reference point moving at angular velocity `omega will be equal to the magnitude `omega * A of the velocity of the reference point.
If we place the velocity vector on an x-y coordinate system, `omega t will therefore be the angle of the velocity vector with the y axis.
The acceleration vector is in the opposite direction to the radial line from the center of the circle to the reference point.
We now look at how the energy of a simple harmonic oscillator depends on its position.
- Recall that this is obtained from the fact that the force required to displace the oscillator to position x changes linearly from 0 to kx as the oscillator moves from equilibrium to this position, so the average force is 1/2 kx.
- Applying this average force through distance x requires work Fave * x = 1/2 k x^2)
It follows that the maximum potential energy of the oscillator occurs at its maximum displacement x = A from equilibrium.
It follows that as the oscillator moves from its maximum displacement A to position x, its potential energy changes from .5 k A^2 to .5 k x^2.
Intuitively, conservation of energy therefore tells us that kinetic energy will increase by this amount.
- `dKE = - `dPE = -.5k (x^2 - A^2) = .5k (A^2 - x^2).
Thus we see that if v is a velocity at position x, we have .5 mv^2 = .5 k (A^2 - x^2). We easily solve this for v to obtain
- v = `sqrt(k/m) `sqrt(A^2 - x^2).
We summarize this solution below, noting that a linear restoring force F = - kx and a maximum displacement A from equilibrium imply the velocity function v(x) = `sqrt(k/m) `sqrt(A^2 - x^2).
- v(x) = vMax `sqrt( 1 - (x/A)^2).
The expression v(x) = vMax `sqrt( 1 - (x/A)^2) gives us to velocity in terms of the maximum velocity vMax and the proportion factor `sqrt( 1 - (x/A)^2).
Halfway from equilibrium to the maximum position, x = 1/2 A and x / A = 1/2.
We can easily test this with our 1.5 m pendulum by placing the barrier halfway between the equilibrium and extreme positions.
Since the pendulum velocity is proportional to the horizontal range, we expect that if we place the barrier halfway between the equilibrium position and the extreme position we will get .87 times the range, or .87 ( 21.5 cm) = 18.7 cm (approximately).
"