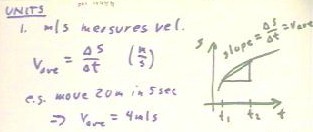
The final exam for Physics 201 and 241 will be generated from the problem banks described in the next paragraph. The final exam for Physics 121 will consist of problems generated from the introductory problem sets. This review is appropriate to each course, each at the appropriate level. Physics 121 students should understand the sections on Units, and Meanings. Physics 201 students should understand the entire review, and Physics 241 students should understand how everything discussed here extends to the context of the calculus-based approach of the course.
The items below consist of questions that will be included with the problem bank on the final exam. They cover most but not all of the main topics of the course. The problem bank will also include the problems used in generating the first and second tests and the major quiz. Other problems will be added to the bank to reflect text problems and topics from the introductory problem set, as appropriate to the level of the course.
Here the questions are divided into four categories: Units, Commonsense Explanations, Meanings and Questions. Each looks at main topics from a different perspective.
The section on Units is concerned with the meanings of the most important units necessary for understanding of first-semester physics. These units are: meter / second, meter / second^2, Newton, Joule, kg m/s, Newton second, watt, radian, meter Newton, kg m^2, rad/sec, and rad/sec^2. On each item you will be expected to explain the meaning of the unit, to specify the most fundamental calculation which gives you that unit, and to give a reference example within the context of which the unit can be understood.
Commonsense Explanations consist of explanations of some of the most important principles encountered in first semester physics. You will be expected to provide clear and correct explanations for these questions.
The Meanings questions are concerned with the meanings of the most important quantities, terms and concepts encountered in first semester physics. You will be expected to express these meanings in your own words.
Questions are posed to further explore the concepts of the course and the ideas used in solving problems.
The questions in these four sections are often redundant in that they often ask things that have been asked in other sections. However, the perspective of each question and each section is slightly different. Hopefully the differences in perspective will enable you to understand different ideas from a variety of perspectives and deepen your knowledge of the subject.
This document covers the sections on Units and on Commonsense Explanations. The sections on Meanings and Questions here include only the statements of the iterms; Review II and Review III cover the remaining items.
1. What does the unit m/s measure?
Velocity is measured in m/s. Average velocity is defined as displacement / time interval.
2. What does the unit m/s^2 measure?
The unit measures acceleration, which is the rate at which velocity changes. Average acceleration is defined as change in velocity / change in clock time.
3. What does the unit Newton measure?
The Newton is a measure of force, defined as the net force required to accelerate a 1 kg mass at 1 m/s^2. In fundamental units, we obtain kg m/s^2, so a Newton is a kg m/s^2.
4. What does the unit Joule measure?
The Joule is a measure of work or energy. Its fundamental definition is in terms of work, which is the product of force and distance.
5. What does the unit watt measure?
The unit watt is a measure of the rate at which work is done, and is equal to a Joule/second.
6. What does the unit radian measure?
A radian is a measure of angle, defined as the central angle of a circle which intercepts an arc whose length is equal to the radius of the circle.
7. What does the unit m N measure?
The unit m N is a measure of torque, which is analogous to force in that can produce angular acceleration or twisting deformation where force produces acceleration or just plane deformation.
8. What does the unit kg m/s measure?
What is the most fundamental calculation you do to understand the unit kg m/s?
What is your reference example for the unit kg m/s?
The unit kg m/s is the measure of the momentum p = mv of an object of mass m moving at velocity v. Momentum can be thought of as the effectiveness of an object in a collision.
9. What does the unit kg m^2 measure?
A kg m^2 is a measure of moment of inertia, which is the resistance of an object to the angular acceleration that results from an applied net torque, in a manner analogous to that in which mass resists the acceleration that results from an applied net force.
10. What does the unit Newton second measure?
The unit N s, or (Newton second), is a measure of the impulse Fave `dt of an average force Fave applied to an object for a time interval `dt. The unit N s is equal to kg m^2 / s^2 * s or to kg m^2 / s.
11. What does the unit radian/second measure?
A radian/second is a measure of angular velocity, which is the change in angular position per unit time.
12. What does the unit radian/second^2 measure?
A radian/second^2 is a measure of angular acceleration, which is the change in angular velocity per unit time.
1. Explain how we develop commonsense notions of motion into the formulation of kinematics.
Our commonsense idea of average velocity is that it is a measure of the average rate at which position changes. The analogous idea of average acceleration is the average rate at which velocity changes. These ideas aren't really common sense, or Western civilization would have arrived at these formulations much earlier. They are sophisticated and complex notions, but we need to understand them until they become common sense.
For uniform acceleration, graphical analysis makes it plausible that the average velocity `ds / `dt over a time interval is equal to the average of the initial and final velocities over that interval, so that vAve = (vf + v0) / 2. Techniques of calculus make this idea rigorously valid. We thus obtain the equality vAve = (vf + v0) / 2. This leads us to the equation `ds = (vf + v0) / 2 * `dt, which we take as one of our two most fundamental equations of uniformly accelerated motion.
For uniform acceleration, the average acceleration `dv / `dt is at any instant just equal to the constant acceleration a, which we express by aAve = a. From this we have `dv / `dt = (vf - v0) / `dt = a, which we rearrange into the form vf = v0 + a `dt. We take this as our second of the two most fundamental equations of uniformly accelerated motion.
From these two equations we derive two additional fundamental equations of uniformly accelerated motion, with the first equation vf^2 = v0^2 + 2 a `ds obtained by eliminating `dt from the two most fundamental equations, and the second equation `ds = v0 `dt + 1/2 a `dt^2 obtained by eliminating vf from the two most fundamental equations.
Using these equations, given any three of the variables v0, vf, `ds, a and `dt we can easily determine the values of the other two.
241 students should understand this development in terms of the definitions v = dx/dt and a = dv/dt with appropriate initial conditions.
2. Explain how Newton's First Law gives us the conditions for the equilibrium of an object.
Newton's First Law tells us that when the net force on object is zero its velocity will remain constant. Constant velocity is the defining condition for equilibrium. Thus equilibrium occurs when the net force on an object is 0.
The net force on an object is the vector sum of its net forces in the x, y, and z directions. The net force will be 0 if an only have all three of these components of the net force is zero. Therefore the condition of equilibrium is that the sum of all the forces acting on the object in the x, y and z directions is zero.
These are the conditions for translational equilibrium. To this we can add the condition of rotational equilibrium, which requires that the sum of the torques on object be 0.
3. Explain how Newton's Second Law relates force and mass to kinematics.
Newton's Second Law gives us the relationship between the net force on an object, its mass, and its acceleration. Since acceleration a is one of the five variables in which we express the equations of uniformly accelerated motion, the connection is obvious.
Given force and mass we can find the acceleration, then given any two of the remaining four variables we can find the values of the other two. Or given the values of any three of the four variables v0, vf, `dt and `ds we can find the acceleration and, if we know either the force or the mass, we can then find the other of these two quantities.
4. Explain how Newton's Third Law gives us conservation of momentum in a collision between two objects.
Newton's 3d Law tells us that when an object exerts a force on another, the other object exerts and equal and opposite force on it. Therefore in a collision or other interaction of two masses, the masses exerted equal and opposite forces on one another. It follows that the impulse F `dt of one object on the other is equal of opposite to that of the other on it. Since the impulse of a force is equal to the change in the momentum of the object on which the forces applied, we find that the two objects experience equal and opposite changes in momentum.
It follows that in a closed system, where the only forces are exerted in action-reaction pairs by objects of the system on one another, the total momentum must remain constant.
5. Explain how the image of gravitational flux helps us understand Newton's inverse-square law of universal gravitation.
If the total gravitational flux associated with a mass is constant, then at greater and greater distances from the object the flux is spread uniformly over the surfaces of spheres of greater and greater radius, each sphere concentric with the center of mass of the object. Since the area of a sphere is proportional to the square of its radius, the field strength g = flux / area of the gravitational field must be inversely proportional to the square of the distance from the center of mass of the object.
As in the figure below, we can derive Newton's Law of Universal Gravitational from the flux picture. Here we see that the force exerted on a mass m2 by a mass m must, by the flux picture, be F = G m m2 / r^2. To complete the statement of the law we need also to show that the force exerted on the mass m by the mass m2 has the same magnitude, and that the force is directed along a line between the two centers of mass. We show the former by the same means as illustrated here, starting with the gravitational flux of the mass m2 and proceeding in the obvious matter. The direction of the force follows from symmetry arguments.
6. State and explain the work/energy theorem relating the kinetic and potential energies of and work done by a system.
The work-energy theorem is a consequence of Newton's Laws of Motion. It states that if a system is isolated, so that no work is done on or by the system, then the total kinetic and potential energy of the system must be constant and as a consequence to total change in kinetic and potential energies from one state of the system to another must be zero. A result of this is that the change `dKE in kinetic energy is equal and opposite to the change `dPE in potential energy. Intuitively this tells us that kinetic energy increases only at the expense of potential energy, potential energy decreases only by increasing kinetic energy (and of course the kinetic energy decreases only when potential energy increases and that potential energy increases only when kinetic energy decreases).
If work `dW is done by the system (or on the system, in which case negative work is done by the system), it is associated with the corresponding change in the sum of kinetic and potential energies, so that `dKE + `dPE = -`dW. If a system does positive work, this relationship tells us that the sum of the kinetic and potential energies decreases by amount equal to work done; the work is done at the expense of the total kinetic and potential energy. If work is done on the system, so that `dW is negative, the result would be an increase in kinetic and potential energies; work done on a system increases the total kinetic and potential energy.
If work `dW is done by the system (or on the system, in which case negative work is done by the system), it is associated with the corresponding change in the sum of kinetic and potential energies, so that `dKE + `dPE = -`dW. If a system does positive work, this relationship tells us that the sum of the kinetic and potential energies decreases by amount equal to work done; the work is done at the expense of the total kinetic and potential energy. If work is done on the system, so that `dW is negative, the result would be an increase in kinetic and potential energies; work done on a system increases the total kinetic and potential energy.
7. Explain how the impulse-momentum theorem implies conservation of momentum in a closed system.
In a closed system, where no forces from outside the system can have any influence, the only forces are those exerted on objects in the system by other objects in the system. By Newton's Third Law, when any two objects interact the force on one is equal and opposite to the force on the other. It follows that the impulses F `dt of these forces are equal and opposite. Hence the resulting changes in the momenta of the two objects are equal and opposite, and the net change in momentum is zero. Since all forces in a closed system arise from the interactions of objects with one another, it follows that the total momentum of the system cannot change.
8. Explain how we use the concepts of centripetal acceleration and gravitational field strength to determine the orbital velocity of a satellite in a circular orbit at a given distance from the center of a planet of given mass.
An object moving in a circle must by Newton's First Law experience a net force, since it is not moving in a straight line at constant velocity. This net force results in an acceleration, by Newton's Second Law. This acceleration is found by analysis of the changes in vector velocities to be perpendicular to the direction of motion of the object, and hence directed toward the center of the circle (hence the name 'centripetal').
For an object in a circular orbit about a planet, this centripetal acceleration is that of the gravitational field, which is directed toward the center of the planet and hence toward the center of the circular orbit. Thus the centripetal acceleration v^2 / r of the object is equal to the gravitational field strength G M / r^2 of the planet (here, v is the orbital velocity, r the orbital radius and M the mass of the planet).
By setting the two expressions for the centripetal acceleration equal, we can solve for v in terms of r and given quantites.
9. Explain how the gravitational potential energy of an object changes as we move away from a planet, and how we obtain these changes.
The gravitational field strength G M / r^2 determines the force on a given mass at a distance r from planet center, as it moves away from a planet. This force changes as r changes. We can determine the approximate average field strength between two distances by averaging the strengths at the two distances; this average will not give the actual average force, due to the nonlinearity of the force as a function of r. We will be reasonably close to the actual average if the ratio of the two distances is not too great (e.g., if the ratio is less than 2 the error will be less than 20%; if the ratio is less than 1.5 the error is less than 8% and if the ratio is less than 1.25 the error is less than 3%).
These changes can be observed with the orbital simulation program by giving the satellite different kinetic energies and directing it away from the planet; the distance traveled before falling back to the planet corresponds to a PE difference equal to the initial KE.
We can use calculus to essentially sum over an infinite number of tiny distance increments, from which we determine that for a mass m moving from distance r1 to distance r2 the work required is `dW = [ G M * (1/r1 - 1/r2) ] * m. 241 students should of course be able to derive this result.
1. What is the meaning of velocity, what is your fundamental example of this quantity, and in what units is it measured?
2. What is the meaning of acceleration, what is your fundamental example of this quantity, and in what units is it measured?
3. What is the meaning of force, what is your fundamental example of this quantity, and in what units is it measured?
4. What is the meaning of kinetic energy, what is your fundamental example of this quantity, and in what units is it measured?
5. What is the meaning of work, what is your fundamental example of this quantity, and in what units is it measured?
6. What is the meaning of potential energy, what is your fundamental example of this quantity, and in what units is it measured?
7. What is the meaning of elastic potential energy, what is your fundamental example of this quantity, and in what units is it measured?
8. What is the meaning of impulse, what is your fundamental example of this quantity, and in what units is it measured?
9. What is the meaning of momentum, what is your fundamental example of this quantity, and in what units is it measured?
10. What is the meaning of moment of inertia, what is your fundamental example of this quantity, and in what units is it measured?
11. What is the meaning of torque, what is your fundamental example of this quantity, and in what units is it measured?
12. What is the meaning of angular position, what is your fundamental example of this quantity, and in what units is it measured?
13. What is the meaning of angular velocity, what is your fundamental example of this quantity, and in what units is it measured?
14. What is the meaning of angular acceleration, what is your fundamental example of this quantity, and in what units is it measured?
15. What is the meaning of angular kinetic energy, what is your fundamental example of this quantity, and in what units is it measured?
16. What is the meaning of the unit of gravitational field, what is your fundamental example of this quantity, and in what units is it measured?
17. What is the meaning of the unit of gravitational flux, what is your fundamental example of this quantity, and in what units is it measured?
18. What is the meaning of force components, what is your fundamental example of this quantity, and in what units is it measured?
19. What is the meaning of velocity components, what is your fundamental example of this quantity, and in what units is it measured?
1. What are the quantities we use to develop our understanding of uniformly accelerated motion, and in terms of which of these quantities can we formulate the equations governing uniformly accelerated motion?
2. In terms of what quantities do we understand motion in a circle?
3. What are the conditions for and the fundamental relationships governing uniformly accelerated motion?
4. What are our fundamental premises in analyzing projectile motion?
5. How does our analysis of the forces on a freely swinging pendulum lead us to the conclusion that a pendulum must undergo simple harmonic motion?
6. How does the circular model give us the position, velocity and acceleration functions for simple harmonic motion?
7. What is the most fundamental premise we make in analyzing vector quantities?
8. What are the vector quantities we study in mechanics?
9. How do we analyze the forces that typically acton an object on an incline?
10. Why is it that the acceleration of an object on an incline is a linear function of slope, provided the angle of the incline is small?
11. How can we observe conservation of energy for objects moving up and down inclines?
12. How can we observe conservation of energy for the interaction between descending objects and rotating objects?
13. How does energy conservation help us understand the behavior of objects moving in response to linear restoring forces?
14. What is the direction of the torque, angular velocity, angular acceleration and angular momentum vectors, and how to these quantities interact as vector quantities?