1. What is the meaning of velocity, what is your fundamental example of this quantity, and in what units is it measured?

Velocity is the rate at which position changes, which can be thought of as the displacement per unit time, with standard units of meters/second. Velocity is a vector quantity; velocity along a straight line is either in the positive or negative direction. This is in contrast with speed, which is the absolute value or magnitude of velocity and is always positive.

Your fundamental example of this quantity should be simple and easy to visualize. We might visualize a position change of 20 meters taking place in 4 seconds, which gives us an average velocity of 5 meters/second.

A slightly more complex example might postulate motion along the x axis from x = 35 m to x = 15 m, taking place in 4 seconds. In this case the displacement is -20 meters so the average velocity is vAve = `ds / `dt = -20 m / 5 sec = -4 m/s.

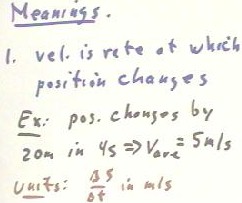
2. What is the meaning of acceleration, what is your fundamental example of this quantity, and in what units is it measured?

Acceleration is the rate at which velocity changes, and can be thought of as the change of velocity per unit time, with standard units of `dv / `dt = m/s / s = m/s^2. Since velocity is a vector quantity, change in velocity will be a vector quantity and therefore acceleration will be a vector quantity.

A fundamental example might be an automobile accelerating from 5 meters/second to 20 meters/second in three seconds. The change in velocity would be 15 m/s, so the average acceleration would be aAve = `dv / `dt = 15 m/s / (3 s) = 5 m/s^2.

Note that when an object accelerates along a straight line, acceleration is in the same direction as velocity when the object is speeding up and in the opposite direction when the object is slowing down. For example, when an object is moving in the negative direction and slowing down, its acceleration would be positive.

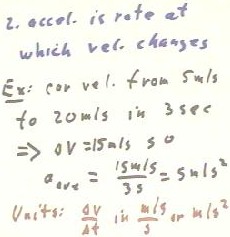
3. What is the meaning of force, what is your fundamental example of this quantity, and in what units is it measured?

A force is something that accelerates and/or deforms objects it acts upon. By Newton's First Law, if and object deviates from stationery or straight-line motion it is because a force is acting upon it. By Newton's Second Law, the acceleration of an object of mass m when subjected to a net force F is a = F / m.

As an example, a 5 kg mass accelerating at 10 meters/second^2 requires a force of (5 kg) * (10 m/s^2) = 50 Newtons. The unit of force is the Newton, which as implicit in the above example reduces to fundamental units of kg m / s^2.

4. What is the meaning of kinetic energy, what is your fundamental example of this quantity, and in what units is it measured?

The kinetic energy of an object of mass m and velocity vf has been defined as the work required by a net force to accelerate a mass from velocity v = 0 to v = vf. Working through the details of this definition we see that this kinetic energy must therefore be KE = 1/2 m v^2. An essential idea of the kinetic energy concept is that it requires an equal amount of work to stop the object; thus the object will do this much work on whatever is stopping it. This allows us to recapture the work done to achieve the object's kinetic energy, at least in principle (practically we can recapture a significant portion of this energy), by doing work on another object (and perhaps increasing its KE).

As a fundamental example we might consider the 2 kg mass moving at a velocity of 5 m/s. It's kinetic energy will be 25 J, as depicted in the figure below. As seen in the calculation the units of kinetic energy are kg m^2 / s^2, which can be expressed as (kg m / s^2) * m or as N m, or Joules.

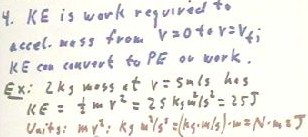
5. What is the meaning of work, what is your fundamental example of this quantity, and in what units is it measured?

Work is defined as the product of the force component parallel to the direction of motion and the distance through which the force is exerted. Directing a net constant force F on a mass m through distance `ds will result in a change of the quantity 1/2 mv^2 which is equal to F `ds; we call 1/2 mv^2 the kinetic energy of the object and F `ds the work done by the net force, and say that the changing kinetic energy is equal to the work done by the net force. Alternatively, applying a vertical force F equal to the weight of object as the object rises through distance `dy, the work done is F `dy = mg `dy; if the object is then dropped and falls under only the force of gravity, gravity will do work mg `dy and kinetic energy 1/2 mv^2 of the object will as a result increase by this amount.

As a fundamental example of work, if we apply a 200 Newton force (about 45 lb) in the direction of motion as we dragg an object 100 m, we do `dW = F `ds = 20,000 N m = 20,000 Joules of work. This unit reduces to N m = kg m / s^2 * m = kg m^2 / s^2.

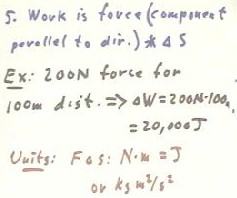
When force is variable in magnitude and/or direction, we can approximate work by summing up Fave `ds totals over small increments `ds increments of displacement, over each of which the force does not vary much.  This is, for example, necessary in determining the work required to lift an object a significant distance above the surface of a planet, since at significant distances gravitational forces undergo significant changes.  As another example, the force required to move against a steady strong wind changes as we change our direction of motion, and for each step we only count the component of the wind's force parallel to our direction of motion.

241 students should understand how this process leads to the integral definition of work as the integral of F ds.

http://youtu.be/WdB8n2EwdCw

6. What is the meaning of potential energy, what is your fundamental example of this quantity, and in what units is it measured?

The gravitational potential energy at a given position is the work required against gravity to displace an object from some reference position, at which the potential energy is taken to be zero, to the given position. For example, we often take ground level as the reference position, where potential energy is zero. To raise an object of mass m a distance h above the ground, we must exert a force equal and opposite to the force mg of gravity on the object for a distance h parallel to that force (e.g., in the vertical direction). The work required is mg h, so relative to the ground the potential energy at height h is mg h.

We often speak of the change in the gravitational potential energy between two positions. For example if we raise an object of mass m near the surface of the earth through a distance `dy, we exert a force mg in the direction of `dy and the work done is mg `dy, which is the change in potential energy between the two points. Thus we say that `dPE = m g `dy.

A fundamental example might be to raise a 100 kg mass through a vertical distance of 50 meters. The force required is 100 kg * 9.8 m/s^2 = 980 N. Applying this force through distance of 50 meters requires work `dW = 980 N * 50 m = 49,000 J. Thus the change in potential energy is `dPE = `dW = 49,000 J. It is good to keep in mind that if the object is then dropped and falls without the interference of dissipative or other forces, when it reaches its original point gravity will have done 49,000 J of work audit and it will have attained a kinetic energy of 49,000 J.

241 students should understand the integral definition of potential energy changes due to changing gravitational field strengths in the vicinity of a planet.

7. What is the meaning of elastic potential energy, what is your fundamental example of this quantity, and in what units is it measured?

The elastic potential energy of an object at a given position is the work required to stretch the (implicit) elastic restraining mechanism from its equilibrium position to the given position. In the usual case, where the elastic restraining mechanism exerts a force F = - kx when displaced x units of distance from its equilibrium position, this work is easily calculated to be Fave * `dx = 1/2 kx * x = 1/2 k x^2.

A possible fundamental example is the work required to stretch a spring whose force constant is k = 1000 N/m from its equilibrium position, at which we set x = 0, to position x = 3 meters. The forces at x = 0 and x = 3 meters are 0 and 3000 N, respectively, so the average force is Fave = 1500 N. The work done to stretch the spring is therefore `dW = Fave * `ds = 1500 N * 3 m = 4500 Joules. This is the elastic potential energy of the spring.

Alternatively, we calculate this potential energy as PE = .5 k x^2 = .5 (1000 N/m) (3m)^2 = 4500 N m = 4500 J. Note that this is the same calculation done to derive the expression .5 kx^2.

The units of elastic potential energy are units of k x^2; since the units of k are N / m and those of x are meters, the units of k x^2 are N/m * m^2 = N m = Joules.

8. What is the meaning of impulse, what is your fundamental example of this quantity, and in what units is it measured?

The impulse of a force is the product of the average force and the time over which the force is applied. The idea is that the grater a force and the longer it is applied, the greater will be its effect.

(Note that Newton's Second Law F = ma can be multiplied by `dt to give us F `dt = m a `dt = m(a `dt) = m `dv; F `dt is the impulse of the force and m `dv the change in the momentum of a constant mass m. F `dt = m `dv is a statement of the impulse-momentum theorem in the special case of a constant mass).

As a fundamental and somewhat vivid example we might consider a golf ball colliding with an individual's skull (which usually causes painful but seldom serious injury), exerting an average force of 2000 N during a .005 sec time of contact. The impulse of this force is 2000 Newtons * .065 s = 10 N s = ... = 10 kg m/s. Note that the units are those of momentum.

The units of impulse are N s, or kg m/s.

241 students should understand the definition of impulse as the integral of F dt over the time interval during which the collision occurs, and should understand that change in momentum mv is not always m `dv, since m might also change; `d(mv) = m `dv + v `dm, by the product rule.

9. What is the meaning of momentum, what is your fundamental example of this quantity, and in what units is it measured?

Momentum can be simply defined as the product mv of the mass of an object in its velocity. A more dynamic definition might be that momentum is the quantity the changes as a result of impulse. By the impulse-momentum theorem we can easily show that momentum must be conserved in a close to system, since in such a system an impulse must buy Newton's 3d Law be accompanied by an equal and opposite impulse, which implies equal and opposite momentum changes.

As an example of momentum we can consider the skull in the preceding problem. If it has a constant mass of 6 kg, then its momentum change m `dv will be m`dv = 10 kg m/s, so that `dv = 10 kg m/s / 6 kg = 1.67 m/s.

The units of momentum are the same as those of impulse, kg m/s.

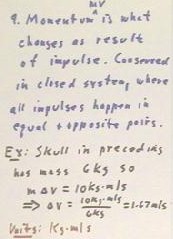
http://youtu.be/BQPn1dqGjUc

10. What is the meaning of moment of inertia, what is your fundamental example of this quantity, and in what units is it measured?

The moment of inertia of an object is thought of as the resistance of an object constrained to rotate about some axis to angular acceleration about that axis, in much the same way that a greater mass better resists attempts to accelerate it (a greater resistance to acceleration implies not greater ability to remain stationary but a lesser acceleration for a given force).

More specifically we say that the moment of inertia is the sum of all the mr^2 contributions of all the masses comprising the object, where r is taken to be the distance of the mass contribution m from the axis of rotation of the object. A more rigorous definition would be the limiting value of the sum of all the `dm r^2 contributions when the object is chopped into tiny pieces with masses `dm. 241 students should understand how this process leads to the integral definition of moment of inertia.

As a fundamental example we might consider a group of radius 1.5 meters and mass 3 kg rotating about an axis through its center. All of its mass is at the same 1.5 m distance from the axis of rotation, so all the mr^2 contributions will have the same r. Thus the moment of inertia is I = mr^2 = 3 kg (1.5m)^2 = 6.75 kg m^2.

A related example is that of a disk, where the mass is uniformly distributed between the center and the outer rim of the disk. The moment of inertia of a disk is obtained using calculus (241 students should be able to derive this formula), and is 1/2 M R^2. If the disk as the same mass and radius as the open the preceding example, it turns out that the moment of inertia will be half that found in that example, or 3.375 kg m^2.

The units of moment of inertia are kg m^2.

11. What is the meaning of torque, what is your fundamental example of this quantity, and in what units is it measured?

12. What is the meaning of angular position, what is your fundamental example of this quantity, and in what units is it measured?

13. What is the meaning of angular velocity, what is your fundamental example of this quantity, and in what units is it measured?

14. What is the meaning of angular acceleration, what is your fundamental example of this quantity, and in what units is it measured?

15. What is the meaning of angular kinetic energy, what is your fundamental example of this quantity, and in what units is it measured?

16. What is the meaning of the unit of gravitational field, what is your fundamental example of this quantity, and in what units is it measured?

17. What is the meaning of the unit of gravitational flux, what is your fundamental example of this quantity, and in what units is it measured?

18. What is the meaning of force components, what is your fundamental example of this quantity, and in what units is it measured?

1. What are the quantities we use to develop our understanding of uniformly accelerated motion, and in terms of which of these quantities can we formulate the equations governing uniformly accelerated motion?

We understand uniformly accelerated motion in terms of the relationships among change of position `ds, time interval `dt, change of velocity `dv, average velocity vAve, initial velocity v0, final velocity vf, and acceleration a.

We formulate uniformly accelerated motion in terms of only five of these quantities, v0, vf, a, `ds and `dt. This formulation permits us to find from the values of any three of these quantities the values of the remaining two. We could have used other combinations of the seven quantities in terms of which we understand uniformly accelerated motion, but we choose these because of our definitions of average velocity vAve = (v0 + vf) / 2 and acceleration, which is expressed in terms of `dv = vf - v0 and `dt. Since vAve `dt = `ds, are five variables are chosen to be `ds, `dt, v0, vf and a.

Our equations of uniformly accelerated motion are easily derived in terms of these definitions, and shown elsewhere in this review.

http://youtu.be/5_WBuMs_KFo

2. In terms of what quantities do we understand motion in a circle?

The motion of an object on a circle is naturally associated with its angular position function `theta(t), angular velocity function `omega(t) and angular acceleration function `alpha(t), to the associated position, velocity and acceleration functions s(t), v(t) and a(t) for the object, and with a centripetal acceleration which had any time is equal v^2 / r. The relationships between the angular functions and the position, velocity and acceleration are the result of the definition of the radian as the central angle which intercepts an arc equal to the radius of the circle; these relationships are s = r * `theta, v = r * `omega and a = r * `alpha.

3. What are the conditions for and the fundamental relationships governing uniformly accelerated motion?

Uniform acceleration is the result of a constant net force acting on a constant mass, or alternatively of a net force which is always proportional to a changing mass. In either case a = F / m will remain constant.

The fundamental relationships are as follows:

• Definition of average velocity: `ds = (vf + v0) / 2 * `dt
• Definition of acceleration: vf = v0 + a `dt
• Elimination of `dt from the first two equations: vf^2 = v0^2 + 2 a `ds
• Elimination of vf from the first to equations: `ds = v0 `dt + 1/2 a `dt^2.

4. What are our fundamental premises in analyzing projectile motion?

As a first approximation in any projectile motion problem in this course, we assume that the projectile is under the influence of only one force, that of gravity. This is a good approximation for dense objects moving at relatively low velocities; at higher velocities or for less dense objects air resistance is an inevitable factor in projectile motion, but we ignore it here.

We also use the fact that since velocity is a vector quantity, its components in any two mutually perpendicular directions are independent and may be analyzed independently.

As a result of this assumption, we see that the net force on the projectile is all in the vertical direction. We therefore conclude that the net force in the horizontal direction is 0.

If we let x stand for the horizontal and y for the upward vertical direction, we see therefore that the y acceleration is ay = -g = -9.8 m/s^2, while the x acceleration is 0.

Thus our premise is boil down to the following:

• ay = -g
• ax = 0
• the x and y motions are independent (except that both share the same time interval `dt)

5. How does our analysis of the forces on a freely swinging pendulum lead us to the conclusion that a pendulum must undergo simple harmonic motion?

Simple harmonic motion occurs whenever a fixed mass m is subject to a restoring force of the form Fnet = -kx. This is approximately the case for a pendulum, as long as the amplitude of motion is small enough to keep the oscillations of the pendulum within a small angle of the equilibrium position.

For a freely swinging pendulum we have only two forces acting on the mass of the pendulum. The first force is the gravitational force mg, acting vertically downward and the second the tension T in the string of the pendulum.

For small angles the pendulum moves almost in a horizontal plane and is therefore nearly any state of y equilibrium, so that the vertical component of the tension must be equal and opposite to the weight mg of the mass m. Since the angle is small, this vertical component will not differ much from the actual tension, so that the tension must be nearly equal to mg.

It follows that the x component of the tension, which is in the same proportion to the tension as the displacement from equilibrium to the length of the pendulum, must have magnitude | Tx | = T (x / L) = mg (x / L) = mg / L * x. It is clear that this tension is in the opposite direction to the displacement x from equilibrium, so that Tx = - (m g / L ) x.

Since we are nearly in vertical equilibrium, the only significant net force is this x component of the tension. Thus we have Fnet = -(m g / L) * x.

This net force is therefore of the form Fnet = -k x, with k = m g / L.

http://youtu.be/GczV4XQXV7w

6. How does the circular model give us the position, velocity and acceleration functions for simple harmonic motion?

As depicted below, an object moving at velocity `omega and starting at angular position `theta = 0 at t = 0 will have moved through angular displacement `d`theta = `omega `dt at clock time t, and will therefore have angular position `theta = `omega t.

Its speed will be A `omega, and its velocity will be at a right angle to the radial line. Since the radial line is angle `omega t with respect to the positive x axis, this velocity will therefore be at angle `omega t with the positive y axis.

The acceleration of the object will be its centripetal acceleration v^2 / A = `omega^2 * A. The direction of this acceleration will be opposite to that of the radial line, and therefore at angle `omega t with respect to the negative x axis.

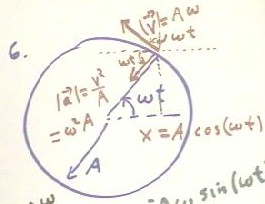
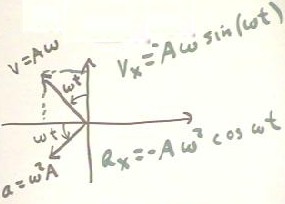
The figure below depicts the velocity and acceleration vectors from the above discussion. Simple trigonometry shows us that these vectors have x components vx = - A `omega sin(`omega t) and ax = - A `omega^2 cos(`omega t). These quantities agree with those obtained by using calculus to obtain the derivatives of the position function x(t) = A cos(`omega t).

7. What is the most fundamental premise we make in analyzing vector quantities?

Our most fundamental premises that any vector quantity is completely equivalent in its effect to the combined effect of its x and y components. That is, if the vector is completely replaced by its x and y components, there will be no change in the behavior of the resulting system.

Thus a force acting in a plane on an object could be replaced by two forces, one in the x and one in the y direction, equal respectively to the x and y components of the original force and no difference could be detected in the behavior of whenever object the forces acting upon.

Or the effect of a velocity, which is a displacement in during time interval `dt, could be replaced by the net displacement in the same time interval corresponding to its x and y velocity components.

Similar statements could be made about any of the vector quantities we study in physics.

http://youtu.be/gir7vmYSijI

8. What are the vector quantities we study in mechanics?

9. How do we analyze the forces that typically acton an object on an incline?

10. Why is it that the acceleration of an object on an incline is a linear function of slope, provided the angle of the incline is small?

11. How can we observe conservation of energy for objects moving up and down inclines?

12. How can we observe conservation of energy for the interaction between descending objects and rotating objects?

13. How does energy conservation help us understand the behavior of objects moving in response to linear restoring forces?