`dt

v0

vf

(v0)

`dt

`dv

vAve

m

a

`ds

`dt

F

`dW

`dp

`dv = vf - v0 triangle:   `dv is change in velocity, v0 and vf are initial and final velocities.

`dv=vf-v0 basic example:   If an automobile increases its velocity from 10 meters / second to 15 meters / second its velocity changes by +5 meters / second.  Here we have

v0 = 10 m/s, vf = 15 m/s so

`dv = vf - v0 = 15 m/s - 10 m/s = 5 m/s.

`dv graphical representation:  If initial velocity is v0 and final velocity is vf the on a graph of v vs. t the change in velocity is represented by the rise of the graph from v0 to vf.

: 

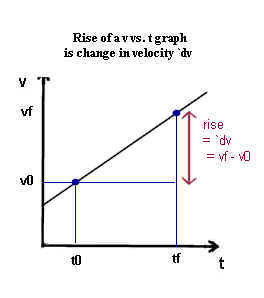vAve :  The definition of average velocity is vAve = `ds / `dt.  If acceleration is uniform then vAve is also equal to the average of initial and final velocities:  vAve = (vf + v0) / 2.

vAve basic example:  If we move through a displacement of 300 miles in 6 hours then our average velocity is 300 miles / (6 hours) = 50 miles / hour.  If our average velocity for a 3-hour trip is 40 miles / hr we move 3 hr * (40 miles / hr) = 120 miles.  If we travel 100 milres at an average of 20 miles/hr then we require 100 mile / (20 miles / hr) = 5 hours to complete the trip.

vAve graphical representation:   vAve = `ds / `dt.  On a graph of s vs. t we see that `ds, the change in position, is represented by the rise of the graph while `dt = tf = t0 is represented by the run, so that vAve = `ds / `dt is represented by the rise / run = slope of the graph.

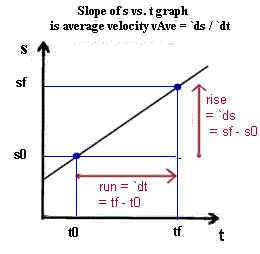
`ds = vAve * `dt.  vAve = `ds / `dt, the average rate of change of position.  From algebraically rearrangemet of this definition we see that `ds = vAve * `dt and that `dt = `ds / vAve.

`ds basic examples:  If we move through a displacement of 300 miles in 6 hours then our average velocity is 300 miles / (6 hours) = 50 miles / hour.  If our average velocity for a 3-hour trip is 40 miles / hr we move 3 hr * (40 miles / hr) = 120 miles.  If we travel 100 milres at an average of 20 miles/hr then we require 100 mile / (20 miles / hr) = 5 hours to complete the trip.

`ds graphical representation:  Since vAve = `ds / `dt is represented by the slope of the s vs. t graph, we see that `ds = vAve * `dt is equal to the product of the slope and the time interval `dt.

a triangle: a is acceleration, which is the rate of change of velocity.  In the case of uniform acceleration we have a = `dv / `dt.  Algebraic rearrangement of this definition gives us `dv = a `dt or `dt = `dv / a.  We also note that `dv = change in velocity, `dv = vf - v0.

acceleration basic examples:  If it requires 10 seconds to increaese the velocity of an automobile by 15 meters per second, then the average acceleration during that time is aAve = `dv / `dt = 15 m/s / (10 s) = 1.5 m/s^2.  If the velocity of a ball rolling down an incline changes at the uniform rate of 2 m/s / s, or 2 m/s^2, then its acceleration is 2 m/s^2; in 5 seconds its velocity will change by `dv = a `dt = 2 m/s^2 * 5 s = 10 m/s. 

Acceleration represented graphically:   On a graph of v vs. t we see that the rise of the graph represents `dv = vf - v0, the change in velocity.  The run represents `dt = tf - t0, the change in clock time.   Acceleration is the rate of change a = `dv / `dt, which is represented by rise / run = `dv / `dt = slope.  Thus acceleration is represented by the slope of a v vs. t graph.

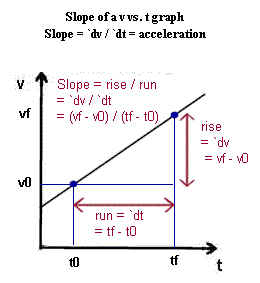
F triangle:  The net force Fnet acting on a system of mass m is equal to the product Fnet = m a of the mass and the acceleration.  Algebraic rearrangement leads to the forms a = Fnet / m, which tells us the acceleration expected from net force Fnet acting on mass m, and m = Fnet / a, from which we can find the mass of an object by observing the acceleration that results from a given force.

F Basic Examples:  To accelerate a mass of 100 kg at 3 m/s^2 requires a net force of Fnet = 100 kg * 3 m/s^2 = 300 Newtons.   A person on the Earth with a mass of 75 kg experiences a force of Fgrav = 75 kg * 9.8 m/s^2 = 735 Newtons as a result of the gravitational force exerted by the Earth.   If we wish to accelerate a rocket with mass 10,000 kg upward at 20 m/s^2 the net force must be 10,000 kg * 20 m/s^2 = 200,000 Newtons; this net force is the sum of the rocket's upward thrust and the 98,000 N downward force exerted by gravity so the thrust must be 200,000 Newtons + 98,000 Newtons.

F graph

`dW triangle

`dW canonical

`dW graph

`dp triangle

`dp canonical

`dp graph

know what the symbols in each formula stand for, conditions under which they apply, canonical example, graph or picture

problems are experiential--they bring the stuff to life and enhance analytical abilities, maybe even lead to self-examined life though it doesn't seem to work for physicists

Forces

Rubber band

Pendulum

Mass on incline

Atwood's machine

Block across floor

Forces in collisions

Work/Energy

Free fall

Incline

Rubber Band

`dKE = `dWnet (block across floor)

Cheerios

Gas tank

Conservative forces

`dKE + `dPE +`dWdiss = `dWappl

Collisions

Reference frames

Two dimensions

Next pages:  Satellites, Rotation, SHM