If an object moves fast for a long time it goes a long ways (a supersonic jet traveling for a few hours can cross the Pacific Ocean).  If the an object moves fast for a short time it can still go pretty far (a bullet will travel the distance of a football field in a fraction of a second).  If an object moves slowly for a long time it can go pretty far (a snail can travel the length of a football field in  a week or so).   If an object moves slowly for a short time it doesn't go far at all (if a snail travels for a fraction of a second you can't even really see its progress).

The graphs below use v vs. t graphs to illustrate what happens if an object moves at a constant fast velocity.

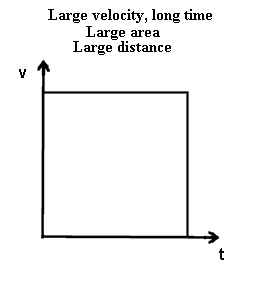
• If an object moves fast at a constant positive velocity then its v vs. t graph will be a straight horizontal line.  If it moves at that velocity for a long time, starting at t = 0, then the straight line will run a long ways in the horizontal direction.  This is depicted by the first graph.
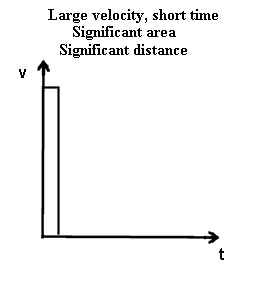
• The second graph depicts the same constant velocity as the first.  However in the case of the second graph the velocity only lasts for a short time, not extending as far in the t direction as the first.

• The distance moved by an object is equal to its speed multiplied by the time interval.   The velocities depicted by the present graphs are positive, and are therefore equal to the speed.
• Note that each graph forms a rectangle. 

• The width of each rectangle represents the time interval, which is greater for the first graph than for the second.
• The height of each rectangle represents the speed of the object.

• It follows that the product of time interval and speed is the represented product of the width and the height of the rectangle.
• Since the product of the width and height of a rectangle is its area, the area of each rectangle represents the distance traveled by the object.

In the case of a fast object moving for a long time the rectangle has much greater area than in the case of a fast object moving for a short time, representing the fact that the first object moves a long ways, the second not as far.

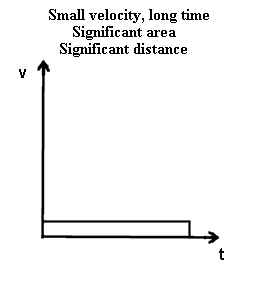
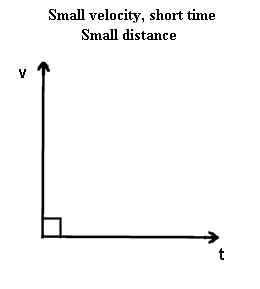
The next two graphs illustrate what happens if an object moves at a constant slow velocity.

• If an object moves slowly at a constant positive velocity then its v vs. t graph is again a straight horizontal line, but the line isn't as far up on the v axis.  If it moves at that velocity for a long time the straight line will still run a long ways in the horizontal direction.  This is depicted by the first graph.
• The second graph depicts the same constant velocity as the first.  In the second graph the velocity only lasts for a short time.

• The areas again represent the product of the speed and the time interval, therefore representing the distances traveled.

In the case of a slow object moving for a long time the rectangle has much greater area than in the case of a slow object moving for a short time, though not nearly as much as in the case of the first graph above where the object moved fast for a long time. 

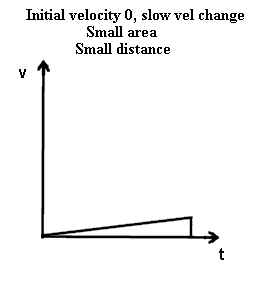
The graphs below show that a slow rate of velocity change does not necessarily imply a small distance.

• In the first graph the object starts at velocity 0 and its velocity changes slowly, so the object never achieves a very great velocity.  You might think of a ball released from rest and rolling down a very gradual incline.
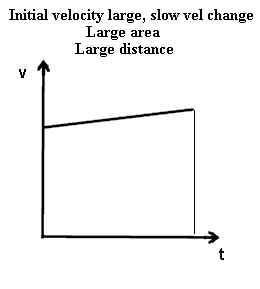
• In the second graph the object starts with a significant positive velocity, which increases slowly (think of a ball started out with a good push before it rolls down a very gradual incline).  In the time interval depicted by the graph the velocity of the object definitely increases, but the increase is smaller than the initial velocity.

• It should be clear that the second object will travel much further since it travels for the same time interval, and since for times in this interval its velocity is always much greater than that of the first.
• Note how the greater distance is revealed by the greater area of the region under the second graph.

We see from this example that the rate at which velocity changes is not directly related to how far it goes.  An object whose velocity changes slowly can move a long ways if it starts out with a significant velocity.

Another way of saying this is that velocity is what affects the distance moved in a time interval, not acceleration.  Acceleration does have an effect, but only indirectly in that acceleration changes velocity.