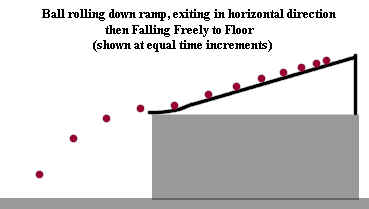
The figure below shows a ball rolling down a ramp then falling to the floor.  The position of the ball is given at regular time intervals.

• While on the ramp the ball travels further during each time interval than during the preceding time interval.  This is due to the constant net force acting on the ball as it travels down the incline.
• After leaving the ramp the ball is subjected to a net force equal to the gravitational force, which acts in the vertical direction.  This vertical net force accelerated the ball in the downward direction, so the distance fallen in the vertical direction is greater with each succeeding time interval.
• Between the ramp and the floor there is no force in the horizontal direction (for now we regard the force of air resistance to be negligible) so the horizontal velocity of the ball doesn't change.  Thus the horizontal displacement of the ball is the same for every time interval.

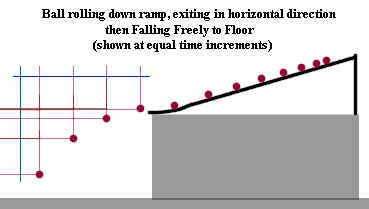
The same situation is depicted in the next picture, but vertical and horizontal projection lines have been added so we can track the motion of the falling object in both directions.

• The horizontal positions are tracked by the vertical projection lines as they cross the horizontal blue line, which represents the x axis.
• We see that the intervals between horizontal positions are uniform, indicating the unchanging velocity in the horizontal direction.
• Another way of saying the same thing is that the x coordinate of the object's position changes by the same amount in equal time intervals, indicating constant velocity in the x direction.

• The vertical positions are tracked by the horizontal projection lines as they cross the vertical blue line, which represents the y axis.
• We see that the intervals between vertical positions increase with every time interval, indicating the changing velocity in the vertical direction.
• We say that the y position of the object changes by increasing amounts with every time interval, indicating a nonzero acceleration in the y direction.

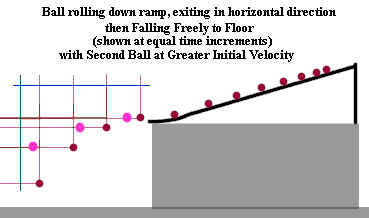
The figure below shows the same ball as in the previous figures, plus a second (slightly larger) ball. The second ball might have rolled down a ramp, or it might have been shot from an air gun, or it might have been started off by some other means, but at the instant the first ball was leaving the ramp moving for an instant solely in the horizontal direction the second ball was right next to it and also moving in the horizontal direction.

The only difference in the motion of the two balls is that the second ball has a greater velocity in the horizontal direction than the first.

• At the end of every time interval the second ball has moved in the horizonal direction about 1.7 times as far as the first, indicating that its horizontal velocity is about 1.7 times that of the first.
• The vertical position of the second ball is however always identical to that of the first.  This is because the vertical position of both balls is the result of zero initial vertical velocity (both balls were initially moving only in the horizontal direction) and the same acceleration resulting from the Earth's gravity.