NOTES ARE IN PROGRESS
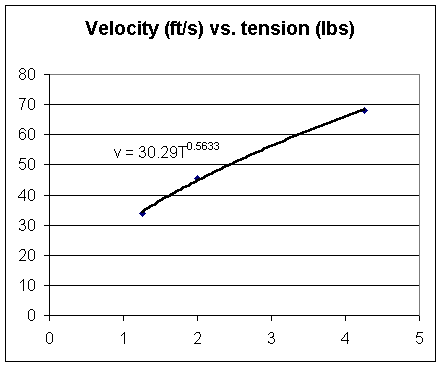
For chain of length 22.75 feet and mass 630 grams we observe that pulse velocity vs. tension appears to satisfy v = 30.3 T^.56, where tension is in lbs.
What we expect is v = sqrt( T / (m/L) ), where T is tension, m is mass and L is length.
| tension (lbs) | vel (ft/sec) |
| 1.25 | 34 |
| 2 | 45.5 |
| 4.25 | 68 |
The figure below depicts a graph of these results and a power-function fit to the graph points.

What velocity would we expect for the first tension?
Using v = sqrt( T / (m/L) ) the result 4.539 was given from class. When asked about the units of the result the response was 'ft / sec'.
However an analysis of the units reveals that the quantities used do not give units of ft/sec, but the mysterious unit of sqrt( lbs / (lbs / ft) ), which comes out sqrt(ft). These are not units of velocity.
The incorrectness of this result comes from failure to use units rigorously in the calculation. Note that the same failure doomed an expensive Mars probe a couple of years ago.
Note that 4.5 does not match up well either with the observed velocity of 34 ft/sec.

The calculation with correct units results in v = 7.66 m/s. This is about 25 ft/s, not far from the 34 ft/s observed (with only one person timing, incidentally).

In general for the given chain we obtain the following expression for v as a function of T.
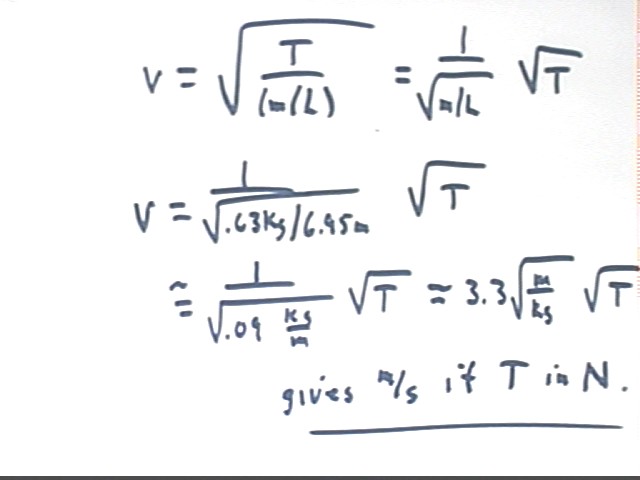
Using a Slinky we observed how a pulse reflects from a stationary object, concluding that the pulse switches sides on reflection as indicated in the figure below.
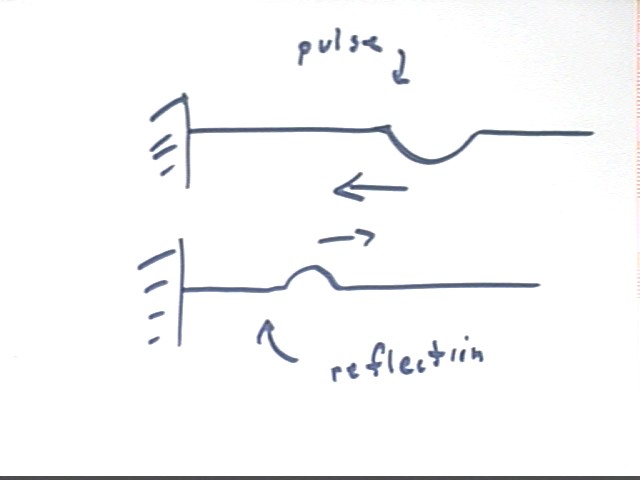
A more gradual pulse will be spread out over a greater length of the Slinky.
If the length of a repeated pulse matches that of the Slinky then the return pulse will 'match up' so that when it is reflected back down the Slinky, it will coincide with the next pulse.
This results in a standing wave in the 'jumprope' mode, where the entire Slinky oscillates back and forth, with every point undergoing simple harmonic motion in phase with every other point.
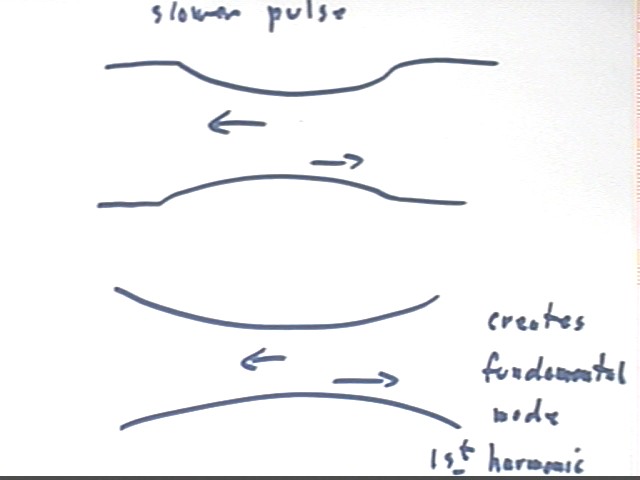
If the pulse is repeated with twice the frequency then the entire cycle will match the length of the Slinky, and when the return pulse is reflected it will again match up with a subsequent pulse.
The result will be a standing wave with half of the Slinky moving to the right while the other moves to the left, and vice versa. This results in a standing wave having nodes, points of very little (ideally no) motion, alternating with antinodes, points where the motion is maximal, as indicated in the lower part of the figure below.
This mode is called the second fundamental. Note again that if the velocity of propagation is the same as for the fundamental, or 'jumprope' mode, the frequency of the pulses must be double that of the fundamental mode.
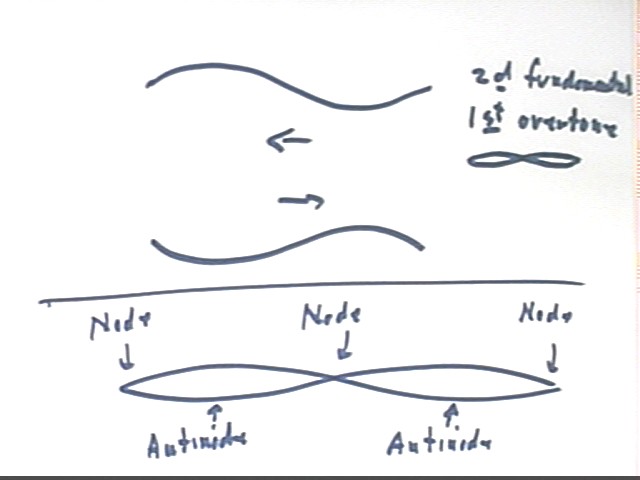
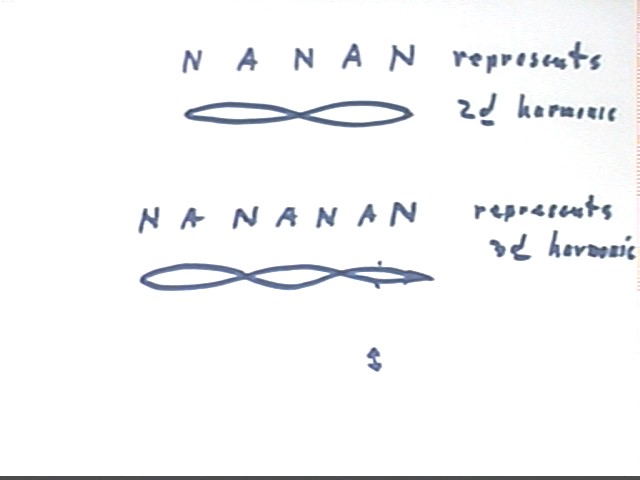
We can abbreviate the node-antinode sequence for the second harmonic as NANAN, as indicated in the figure below.
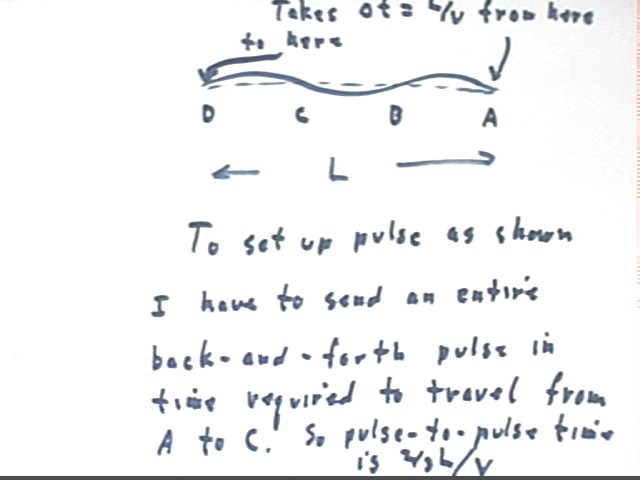
The third harmonic is the next possible mode, which is represented in abbreviated form by NANANAN.
To set up the third harmonic the entire pulse must occur as the wave travels from A to C (since the string from A to C contains the result of a complete cycle of oscillation).
Important Note ****** :
This note was inserted following Problem 3 on the practice test below. It might be best read after seeing the solution to that problem.
`dQ = 5/2 n R `dT is thermal energy required to raise temp of diatomic gas by temp change `dT.
We say Cv = 5/2 R, and `dQ = Cv * n * `dT, where Cv is molar specific heat at constant volume.
At constant pressure we see from the aboe that Cp, the molar specific heat at constant pressure, is 7/2 R.
The ratio Cp / Cv, which for a diatomic gas is
For monatomic gases (only 3 degrees of freedom) we have Cv = 3/2 n R T and Cp = 5/2 n R T, so for a monatomic gas
Note that all this is for ideal gases.
Adiabatic expansion or compression of a gas:
. . . . . . . . . . . . . . . .
Constants:
| k = 9*10^9 N m^2 / C^2 | qE = 1.6 * 10^-19 C | h = 6.63 * 10^-34 J s |
| energy of n=1 orbital in hydrogen atom: -13.6 eV | k ' = 9 * 10^-7 T m / amp | atomic mass unit: 1.66 * 10^-27 kg |
| electron mass: 9.11 * 10^-31 kg | speed of light: 3 * 10^8 m/s | Avogadro's Number: 6.023 * 10^-23 particles/mole |
| Gas Constant: R = 8.31 J / (mole K) | proton mass: 1.6726 * 10^-27 kg | neutron mass: 1.6749 * 10^-27 kg |
Problem Number 1
Assuming that your lungs can function when under a pressure of 7.8 kPa, what is the deepest you could be under water and still breathe through a tube to the surface?
Bernoulli's Eqn applies, with v presumed constant.
Problem Number 2
There is a small amount of water at the bottom of a sealed container of volume 7.6 liters which is otherwise full of an ideal gas. A thin tube open to the atmosphere extends down into the water, and up to a height of 143 cm. The system is initially at atmospheric pressure and temperature 141 Celsius.
Bernoulli's Equation will give us the new pressure.
If the tube is thin then volume change is negligible so PV = nRT tells us that P / T is constant.
From init pressure, final pressure, init temp we easily find final temp.
Problem Number 3
A diatomic gas in a 1.5-liter container is originally at 25 Celsius and atmospheric pressure. It is heated at constant volume until its pressure has increased by .86 atm, then at constant pressure until the gas has increased its volume by .39 liters. How much thermal energy is required? By how much does the internal energy of the gas change? How much work is done in the process?
The rought sketch below is helpful in assembling the information given in this problem.

First state:
Second state:
V const so P/T is const.
We easily find T1.
Third state:
P const so V / T const.
We easily find T2.
Thermal energy changes:
Problem Number 4
Water is descending in a vertical pipe of diameter 8 cm. At a certain level the water flows into a smaller pipe of diameter 1.2 cm. At a certain instant the gauge pressure of the water at a point 80 cm above the narrowing point is 86.6 kPa and the water there is moving at 94 cm/s. What is the gauge pressure of the water just above the narrowing point? What is the pressure change across the narrowing point?

Three points are involved here, the 'known point' 80 cm above, the point just above, and the point just below the narrowing. Number these points 0, 1 and 2. We will apply Bernoulli's Equation to these points, two points at a time..
Problem Number 5
The masses of 1 mole of various gases are as follows: hydrogen about 2 grams, helium about 4 grams, nitrogen about 28 grams, oxygen about 32 grams and carbon dioxide about 44 grams. On the average how fast does a molecule of each gas move at 333 Celsius?
Ave KE per particle is KEave = 3/2 k T.
It follows that .5 m v^2 = 3/2 k T. We easily find v if we just know m.
We know how many grams per mole so we easily find the number of grams per particle.
Problem Number 6
Explain how to use energy considerations to determine the velocity with which water will flow from a hole in a large container if the pressure difference between the inside and outside of the container is 3100 N/m^2, and if the water inside the container is effectively stationary. You may do this symbolically or you may consider the energy changes as a 1-gram mass of water exits the cylinder.
Consider a 'plug' of water with cs area A and length L.
One end of the 'plug' is in the container and experiences the pressure in the container. The other end is exposed to atmospheric pressure.
We can obtain expressions for the net force on the plug, then for the work done in pushing the plug out, so we know the KE of the plug as it exits.
The expression for the volume and therefore the expression for the mass of the plug are easily found.
Setting .5 m v^2 = KE we easily find the expression for v.
The Chain
We note that when held under tension about 170 Newtons (at the ends; the thing sagged purty good in the middle) a chain with total mass about 15 kg and length 8 meters supported a pulse which made 3 round trips in 5.4 seconds.
How fast was the pulse moving?
Round trip is 16 m, total for 3 round trips is 48 m.
48 m / (5.4 sec) = 9 m/s ballpark.
How does this compare with sqrt( tension / (mass per unit length) )?
sqrt( 170 N / (15 kg / 8 m) ) = sqrt( 170 kg m/s^2 / (1.88 kg / m) ) = sqrt(90 m^2 / s^2) = 9.5 m/s.
When you have completed the entire assignment run the Query program.