Mathematics Review:
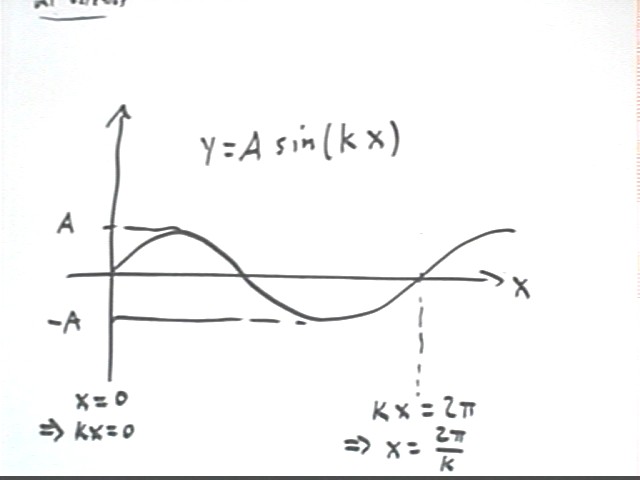
The graph of y = A sin(kx) is a 'sine wave' with amplitude A, completing a cycle as kx changes from 0 to 2 pi.

If 0 < kx < 2 pi then 0 < x < 2 pi / k.
It follows that the wavelength of the wave is lambda = 2 pi / k.

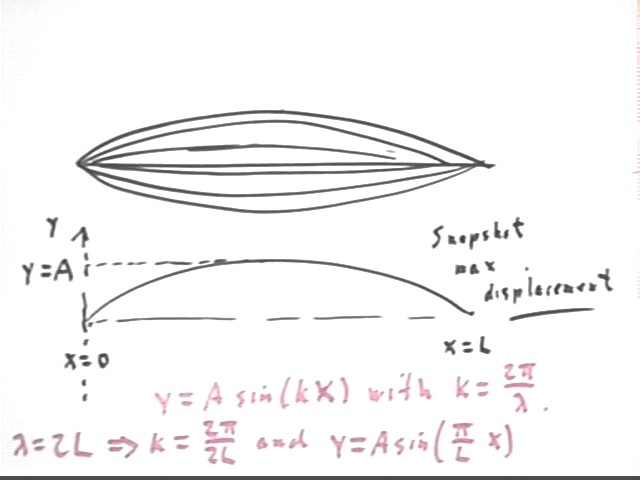
The figure below represents a string vibrating in its fundamental mode, with antinode at the middle and nodes at the ends. The shape of the string is always one 'hump' of a sine wave, corresponding to half of a complete wavelength. The displacement in the middle of the string changes from one instant to another. We can think of the figure as representing successive 'snapshots' a string that starts with its max possible positive displacement, then descends to a straight-line configuration before moving into negative displacements.
The displacement at the antinode is maximized when the string reaches its maximum displacement; we call this maximum displacement A.
As we have seen in previous classes the wavelength associated with this mode of vibration is 2 L, where L is the length of the string.
The graph represents the string in its maximum-positive-displacement configuration, corresponding to antinode displacement A.
The graph therefore represents the function y = A sin ( k x ), where k = 2 pi / (2 L) = pi / L.
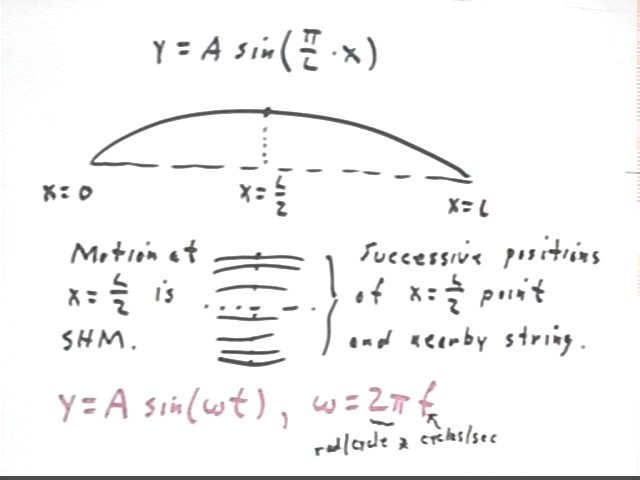
In the figure below we indicate the motion of the center point of the string, at position x = L / 2, as time changes.
The motion of this point is simple harmonic, with angular frequency omega corresponding to the period of the wave (omega = 2 pi f).
Recall, or review, the circular model of simple harmonic motion, which you are expected to know and to apply where needed.
Mathematics interlude: Graph y = A sin(2x) at x = 0, .3, .6, .9, 1.2, 1.5.
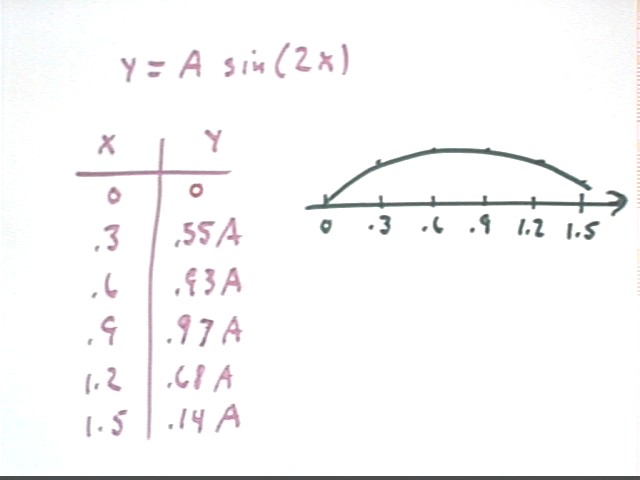
We now consider the motion of the x = 1.38 position on the standing wave whose maximum-displacement graph is y = A sin(2x).
We know the motion of the x = 1.38 point will be SHM with some amplitude. As we've observed, the displacement of the x = 1.38 point on this maximum-displacement snapshot is less than A, so the amplitude of the SHM of this point will be less than A.
What is the amplitude of the SHM at the x = 1.38 point?
The amplitude will be equal to the displacement on the y = A sin(2x) graph at the x = 1.38 point.
What is the equation of motion at the x = 1.38 point?
y = .37 A sin(omega * t).

Consider at the fundamental mode of vibration in a string of length L. What is the equation of motion for a point at arbitrary position x?
The maximum-amplitude graph y = A sin(kx) is shown below.
The point x oscillates with 'local amplitude' A(x) = A sin(k * x) The equation of motion at x is therefore y(t) = A(x) sin(omega t) = A sin( k x ) * sin(omega t).
This equation ends up describing the position y as a function of both position x and time t. We therefore write y(x, t) instead of just y(t) and our equation is
For the fundamental we have k = 2 pi / wavelength = 2 pi / (2 L) = pi / L, and angular frequency omega = v / wavelength = v / (2 L). So the equation for the fundamental can be written

The general equation of motion for a standing wave with amplitude A, wave number k and angular frequency omega is represented below. The equation can be understood as simple harmonic motion with angular frequency omega and local amplitude determined by position x.
UNIVERSITY PHYSICS NOTE: The second partial derivatives of this function should be calculated and their relationship determined.

We see that the second harmonic, at max displacement and amplitude A2, is y = A2 sin(kx) with k now equal to 2 pi / L.
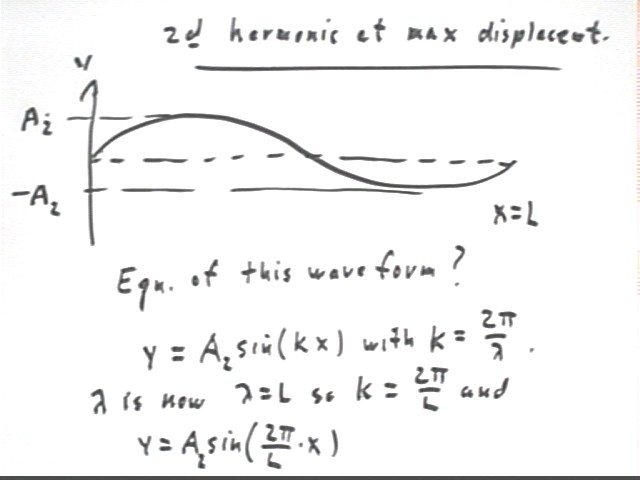
If the angular frequency of the fundamental is omega0 then since the frequency of the second harmonic is double that of the first (this is because the wavelength is half that of the first) the angular frequency of the second harmonic is 2 * omega0.

The general equation of a standing wave in a plucked string contains all possible harmonics.
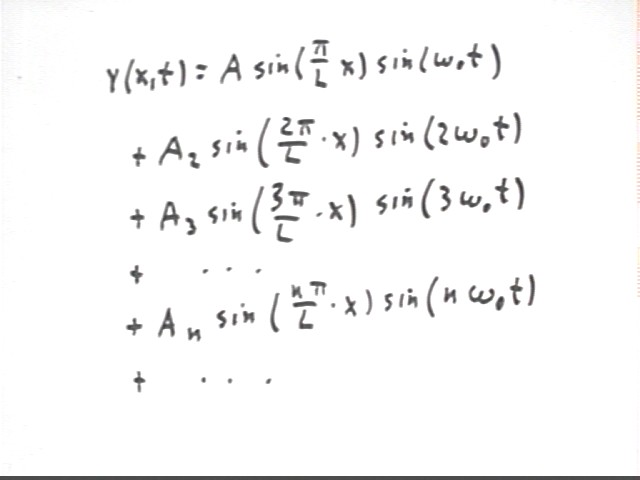
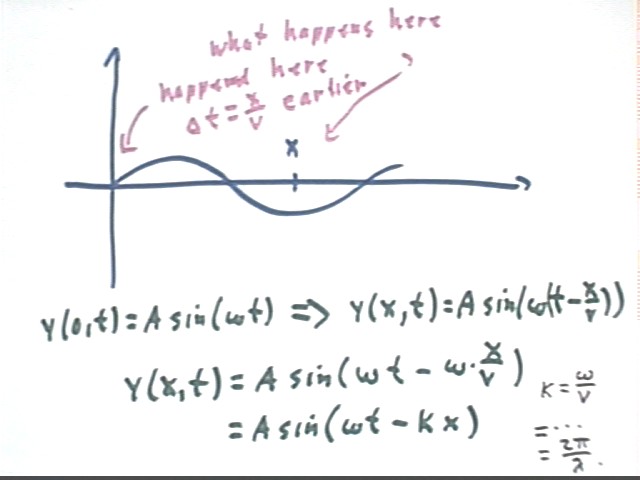
The figure below depicts a traveling wave with propagation velocity v and amplitude A. The x = 0 point is 'driven' in SHM with amplitude A and angular frequency omega, giving us
y(0, t) = A sin(omega * t)/.

We ask what the equation of motion will be at arbitrary position x.
It follows that y(x, t) = A sin(omega * (t - x/v)).
Since k = omega / v this simplifies to the form