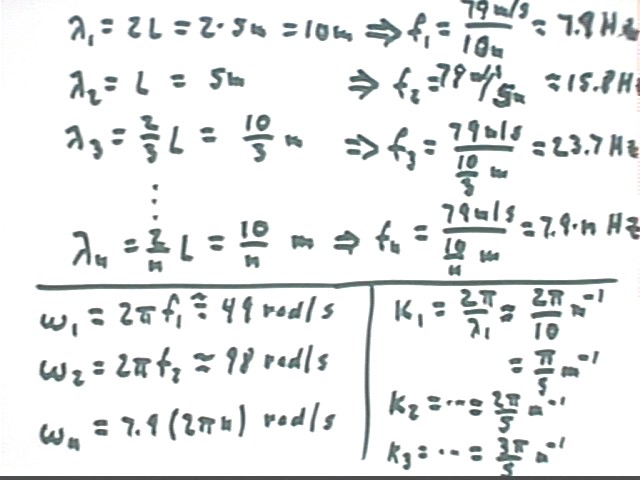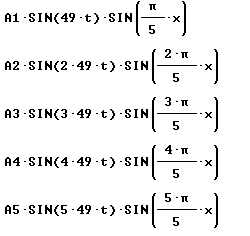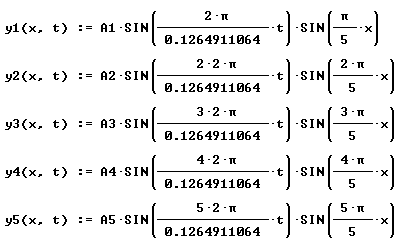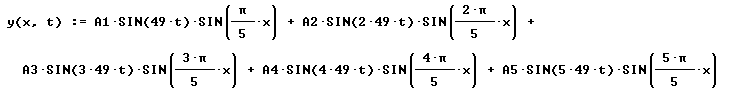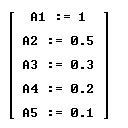Physics II Class 02/26

Find the equation of a standing wave in a string whose mass is 40 grams, length 5 meters under tension 50 Newtons.

We first find the velocity of the wave as indicated below.

We then recall that the node-antinode configuration leads us to the conclusion that the wavelength of the nth harmonic is 2 / n * L.

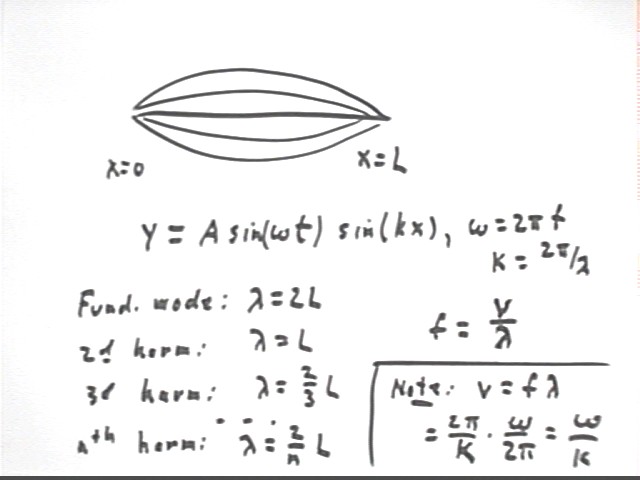
The equation of any harmonic is y = A sin(omega t) sin(k x), where omega = 2 pi f where f = v / lambda and k = 2 pi / lambda.  So if we know the wavelength lambda of the harmonic and the propagation velocity v (the same for all harmonics) we can find the equation of motion for that harmonic.

The propagation velocity v = 79 m/s and the wavelengths 10m, 5 m, 10/3 m, etc. give us frequencies f1, f2, f3, ... of 7.9 Hz, 15.8 Hz, 23.7 Hz, ..., with general frequency 7.9 * n Hz for the nth harmonic.

The angular frequencies omega1, omega2, omega3, etc. are about 49 rad/s, 98 rad/s, etc. with general angular frequency omega(n) = 7.9 * 2 pi n rad/s.  The corresponding wave numbers are k1 = 2 pi / 10 m^-1, k2 = 2 pi / 5 m^-1, and in general kn = 2 pi n / 10 m^-1 = n * pi / 5 m^-1

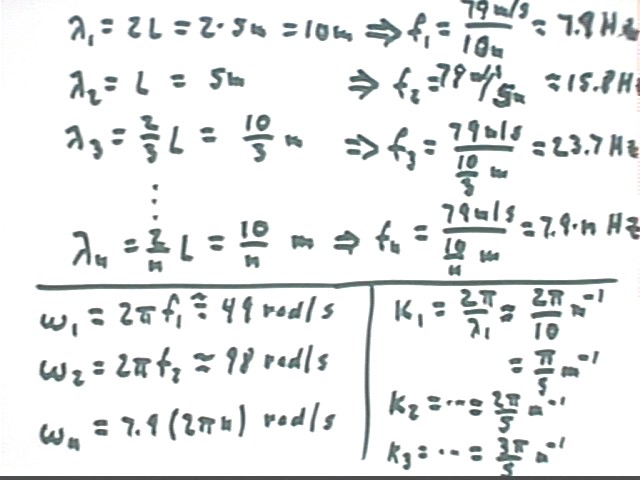
The corresponding waveforms for the first five harmonics are given below:

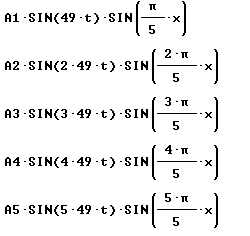
The general equation of the wave standing wave is the superposition of all these harmonics.  Using A1, A2, ... for the amplitudes of the various harmonics we have the general equation shown below.

The harmonics in the figure below are more accurate versions of the above, using the ridiculously accurate 2 pi / 0.1264811064 rad/s instead of the approximation 49 rad/s used above.  Note how the coefficients of the 2 pi in the numerator of the first sine function are 1, 2, 3, 4 and 5, showing how the frequencies of the harmonics increase as multiples of the fundamental frequency.

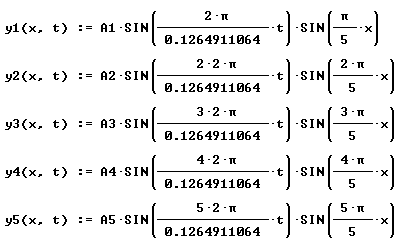
Looking at just the first harmonic y1(x, t) we see that

As t continues to increase the waveform will first reach its maximum antinode displacement A1, then will return to the 'flat' waveform, the will move below the flat waveform to max negative displacement -A1 before returning to the flat waveform and starting the cycle over.

The 2d harmonic y2(x, t) will oscillate as indicated below, with nodes at the endpoints and the midpoint.

This mode of vibration (at twice the frequency of the fundamental) superimposed on the fundamental described above gives us the most familiar behavior of the wave simulation.

If we add the first five harmonics we get the function y(x,t) in the figure below.

 

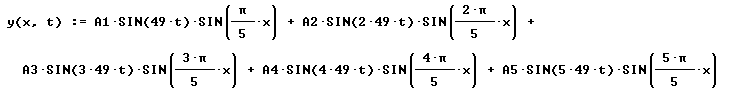
This function can be abbreviated as y(x, t) := y1(x, t) + y2(x, t) + y3(x, t) + y4(x, t) + y5(x, t).

If the values of A1, ..., A5 are set as indicated below,

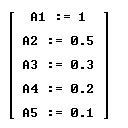
with each harmonic having a bit less amplitude than the preceding, we get the function

Plotting this function from x = 0 to x = 5 gives us the succession of waveforms indicated below:

 

 

 

 

 

 

 

Assignment 14

Assignment 15:

Assignment 16:

Assignment 18:

Assignment 19:

Assignment 25:

Assignment 26: 

Assignment 27: 

Assignment 28:    

Assignment 29: 

Assignment 30: 

Assignment 31: