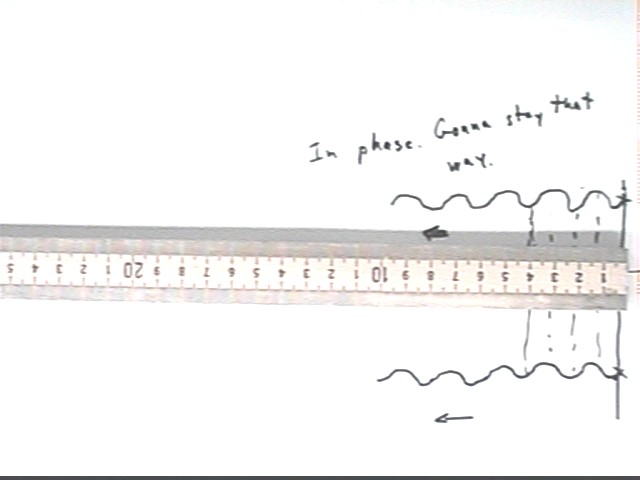
At what angles do 2-cm waves from two sources result in peaks aligning with peaks?
The figure below depicts two waves with wavelength 2 cm emanating in phase from two sources marked by x's at the right side of the figure. The waves move in a direction which is very nearly perpendicular to the line connecting the sources.
We think of the two waves as being not quite parallel but rather meeting at some distant point.
Note how the peaks and valleys of the waves are located directly across from one another.

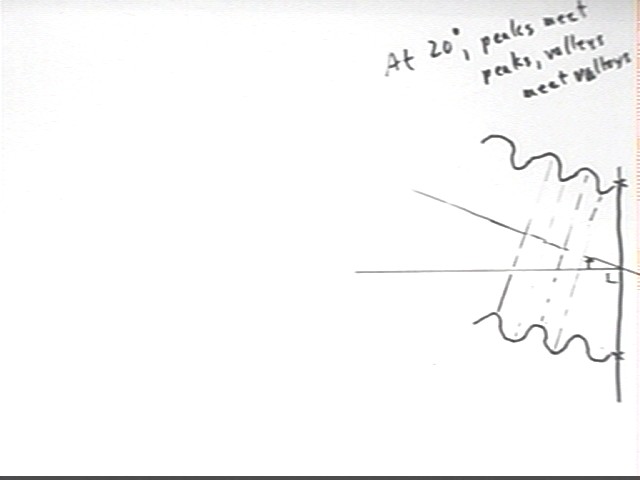
In the next figure the waves are directed at an angle of about 20 deg from the 'perpendicular direction' of the preceding figure (recall that in the preceding figure the direction of the waves was perpendicular to the line connecting the sources).
The direction of all waves will be measured with respect to this perpendicular direction.
Note how the peaks and valleys of the waves again line up relative to the direction of the wave. The dotted lines connecting peaks and valleys are constructed perpendicular to the 20 degree direction of the wave.
Note also how the dotted line that meets the top meter stick at the 2 cm position would meet the lower meter stick at the 4 cm position, and that the 4 cm position on the first meter stick similarly corresponds to the 6 cm position on the second. This leads us to conclude that the bottom wave lags behind the top wave by 2 cm.

The square block in the figure below shows how the 1 cm position of the top wave aligns with the 3 cm position of the bottom wave, reinforcing the idea that the bottom wave lags 2 cm behind the top.
Since 2 cm is equal to the wavelength of the wave, we say that the bottom wave lags the first by 1 wavelength.
If the waves are almost parallel, in fact meeting at some distant point, the since peaks meet peaks and valleys meet valleys the waves will reinforce. This is called constructive interference.

The next figure is the same as the preceding figures but without the meter sticks.
At what angles do 2-cm waves from two sources result in peaks aligning with valleys?
This question was posed as an experimental question. Groups were to try to construct this situation using meter sticks.
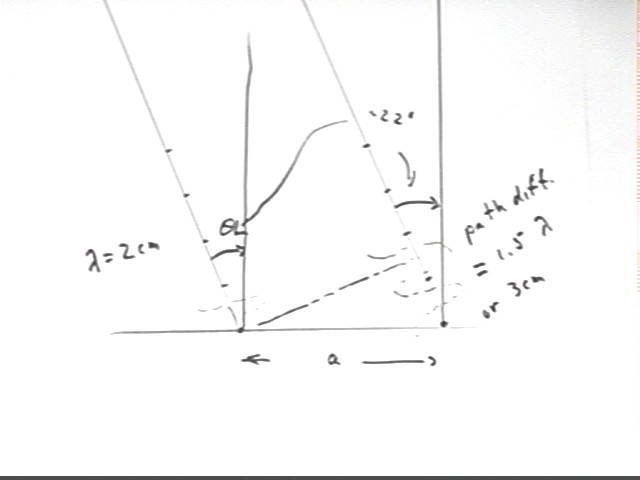
The figure below shows the result of one construction. The lines at 22 degrees are marked at 2 cm intervals, indicating peaks at those positions.
The line segment perpendicular to the wave direction shows how the first peak of the left-hand wave is aligned halfway between peaks of the right-hand wave, meeting a 'valley' of the right-hand wave at a distance of 1.5 wavelengths or 3 cm from the right-hand source.
The right-hand wave therefore lags the left-hand wave by 3 cm or 1.5 wavelengths.
If the waves are considered to be 'almost parallel', meeting at some distant point, the peak-to-valley alignment of these waves results in cancellation of the waves at that meeting point. This is called destructive interference.
Another group, using a 5.8 cm separation of the source points, obtained a 1 cm path difference at an angle of 10 deg and a 2 cm path difference at an angle of 20 deg. We note that
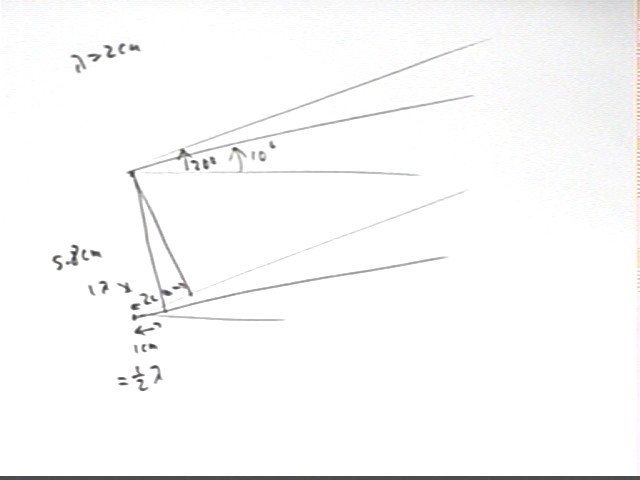
Another group using separation 6 cm obtained a 3 cm path difference at an angle of 21 deg. 3 cm is 1.5 wavelengths and aligns peaks with valleys, resulting in destructive interference.
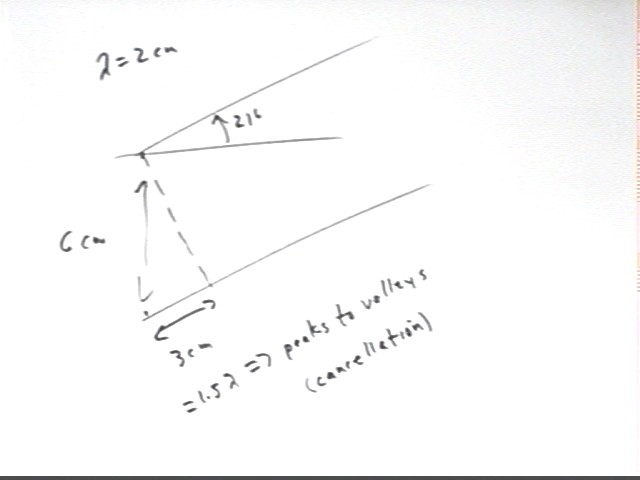
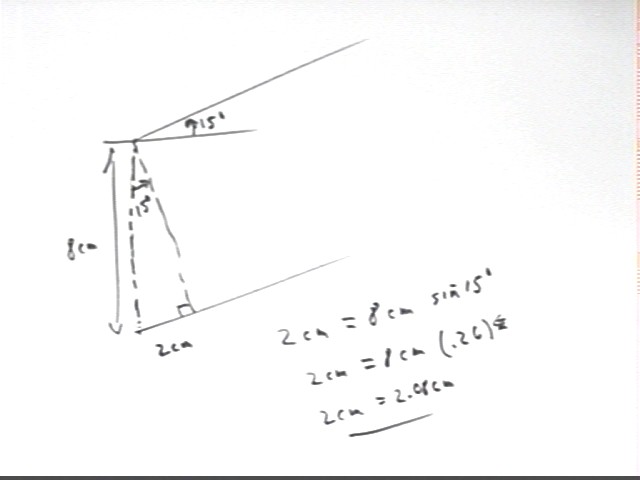
A third group obtained a 2 cm path difference at 15 deg, using an 8 cm separation of sources.
We construct a right triangle with one leg running between the waves and perpendicular to the wave direction, a second leg comprising the path difference and a the hypotenuse equal to the 8 cm separation of the sources.
Since the hypotenuse and longer leg of the triangle are respectively perpendicular to the two lines that form the 15 deg angle at the top of the figure, the angle between hypotenuse and longer leg is also 15 deg.
The path difference is the leg of the triangle opposite the 15 deg angle. The group claimed that the path difference is 2 cm. We see that the leg opposite the 15 deg angle should be 8 cm * sin(15 deg) = 2.08, very close to the 2 cm claimed by the group and validating their construction.
The results for most of the other groups check out very well, and all check out at least fairly well. You should verify this with a construction similar to that used in this example.
The construction below, done carefully by the instructor, used a 19 cm separation of sources and found that an 8 degree angle resulted in a path difference of 3 cm. You should verify that this result is not particularly accurate compared to most result obtained by groups. This is in contrast to the instructor's first figure, not done with any particular care, but which was very accurate. The point here is that there's a good bit of uncertainty in this sort of construction and that all results obtained by students were of good quality.
If light of wavelength 400 nm is split into two 'rays', one of which travels 3600 nm further than the other before joining the first in yore eyeball, are you gonna see it purty good?
Yup. One travels exactly 9 wavelengths further than the other so peaks will meet peaks and valleys will meet valleys on yore retina; the waves reinforce each other and you see them just fine.
What will be the case for light of wavelength 420 nm?
A 420 nm waves will experience a path difference of 3600 nm / (420 nm) = 8.57 wavelengths. At 8.5 wavelengths we get perfect peak-valley alignment, resulting in cancellation and we won't see much of anything. At 8.57 wavelengths the alignment is pretty much peak-to-valley, but the cancellation isn't perfect and we will see something.
Note that 450 nm light will experience a path difference of exactly 8 wavelengths and will reinforce. So we'll see the 400 nm and 450 nm light much better than in-between wavelengths, leading us to perceive two colors and therefore to pretty much miss the colors in between.