Physics II Class 03/12

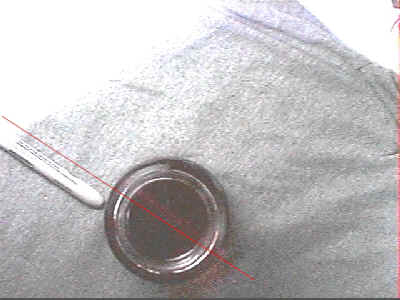
The figure below depicts a laser beam passing through a jar of honey.  The direction of the marker to the left of the jar indicates the direction of the incoming beam.

In the figure below the red line passing through the center of the jar is parallel to the direction of the incoming beam.  We can see how the actual laser beam is refracted toward this beam.

The figure below shows the actual beam passing through the center of the jar.

The next figure shows the red 'direction line' superimposed on the preceding figure, to show that the direction line is indeed parallel to the central beam.

The figure below shows a beam which is fairly close to the central beam

The next figure is identical to the preceding but with the red line indicating the central beam superimposed.

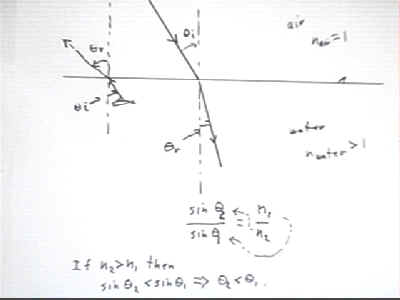
Refraction is first understood in terms of light beams passing from air to water and from water to air, with a smooth horizontal water surface.

• The beam directed from air to water is indicated by the arrows along the beam, indicating that the beam passes from air above to water below.
• The angles theta(i) and theta(r) are measured with respect to the line normal (i.e., perpendicular) to the water-air interface.  theta(i) is called the angle of incidence and theta(r) the angle of refraction.

• For the beam which originates at the fish, near the left side of the figure, the beam passes from air to water so the angle of incidence is measured with respect to the normal line as the beam approaches the water surface from within the water, and the angle of refraction is measured as the beam moves into the air.

The index of refraction of a substance tells us how fast light moves in that substance.

• The speed of light in a vacuum is c = 3.00 * 10^8 m/s, accurate to 3 significant figures.  A more accurate figure is c = 2.998 * 10^8 m/s.
• In a substance with index of refraction n, light travels at speed c / n.

If light travels from a substance with lower index of refraction into a substance with higher index of refraction, the direction of the beam is changed, with the beam deflected toward the normal.

If light travels from a substance with higher index of refraction into a substance with lower index of refraction, the direction of the beam is changed, with the beam deflected away from the normal.

• The index of refraction of air is nearly 1, while the index of refraction of water is significantly higher than 1.  
• Therefore light beams passing from air to water are deflected toward normal and those passing from water to air are deflected away from normal.

The general rule is that for a beam passing the interface between two substances with indices of refraction n1 and n2, the corresponding angles theta1 and theta2 are related to the indices by

• Snell's Law:  sin(theta2) / sin(theta1) = n1 / n2.

Note how the relationship is inverse, with sin(theta2) in the numerator of one fraction and the index n2 of the corresponding substance in the denominator of the other fraction.

• This law tells us that if n2 > n1, then sin(theta2) must be less than sin(theta1).
• Since all angles are between 0 and 90 degrees, a domain on which the sine function is increasing from 0 to 1, it follows that theta2 must be less than theta1.
• Thus if the beam passes between air (lower index) and water (higher index) the angle in water will be less than the angle in air, as is the case in both instances (air into water and water into air) below.

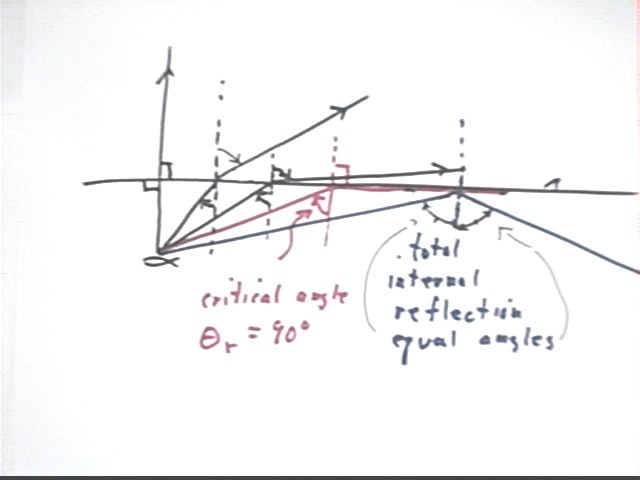
The figure below depicts beams passing from water to air at progressively changing angles of incidence.

• The first beam is vertical, incident at a right angle.
• The next beam makes a significant angle with the surface and is deflected away from the surface at an even greater angle.
• The third beam, incident at a greater angle than the second, is deflected in a direction which is almost parallel to the water.
• The fourth beam, drawn in red, is deflected to a refracted angle of 90 degrees, making it parallel to the water surface.  The incident angle at which this happens is called the critical angle.
• The fifth beam, incident at an angle even greater than the critical angle, would be deflected at an angle greater than 90 degrees if it was able to enter the air.  However this is not the case, since at such an angle the beam could not enter the air.  Such a beam will be completely reflected back into the water, with no loss of energy at the point of reflection (the water itself absorbs some of the beam's energy as the beam passes through the water, but there is no change in energy associated with the reflection itself).
• As with any reflection the beam will be reflected at the same angle to normal as the incident beam. 

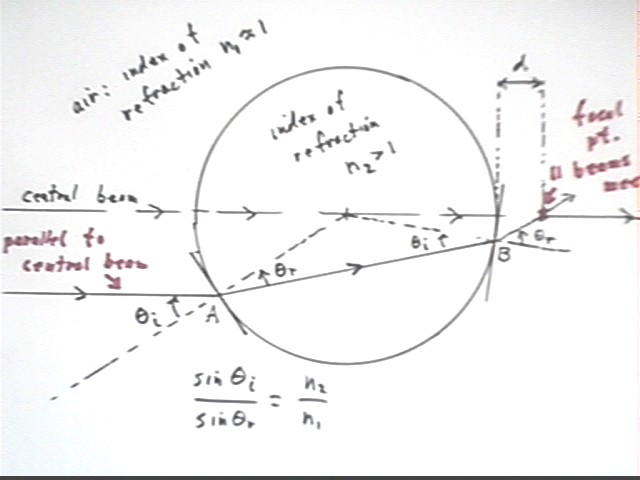
The figure below depicts the situation with light from a distant point source passing through a cylinder filled with a substance whose index of refraction exceeds that of the air.  The beams depicted here are analogous to the laser beams observed passing through the honey jar.

Since the source is assumed to be distant we can think of the light as consisting of a large number of narrow beams, which because of the distance of the source are parallel.

We consider a central beam and a beam which is parallel to the central beam but which passes through the cylinder somewhat below the central beam.

• As the second beam first encounters the cylinder at point A, it interacts only with a very limited part of the cylinder's surface, which in the neighborhood of a thin beam is therefore practially flat. The direction of this flat surface is tangent to the cylinder, so that the normal direction is that of a radial line from the center of the circle to the point at which the beam meets the cylinder.
• The tangent and normal (radial) lines and the angles theta(i) and theta(r) of incidence and refraction at this point are indicated.  We see that the beam is deflected toward the normal line, which bends it slightly toward the central axis of the cylinder.

For a cylinder filled with water, honey, or most types of glass the beam will not cross the central beam before reaching the opposite side of the cylinder.  For some substances (e.g., diamond) the beam will cross the central beam.

Note also that the central beam encounters the cylinder at the normal direction and that its angles of incidence and refraction are therefore zero, so that it passes undeflected through the cylinder.

When the initially 'parallel' beam reaches the opposite end of the cylinder it again encounters a locally flat surface which appears to be parallel to the tangent line at that point.  The angles theta(i) and theta(r) of incidence and refraction are indicated at this point (point B).

• Since the beam passes from a higher to a lower index of refraction its angle of refraction will be greater than its angle of incidence, and it will be deflected away from the normal.  This results in a deflection 'toward' the central angle.
• It turns out that for all parallel beams reasonably close to the central beam, the beam emerging from the cylinder will cross the central beam at the same point.  Beams which enter the cylinder further from the center will miss this point, missing by more and more as the distance from the central beam increases.
• It would be possible to shape a sort of elliptical or parabolic cylinder in such a way that distant beams meet much closer to the center.

We observed light from a candle approximately 2.5 meters away as it was focused by two cylinders, one containing water and the other honey.  From our observations we are able to determine the indices of refraction of these substances.  We note a few sources of small but significant error:

• 2.5 meters is not all that distant, so the beams that were focused are not exactly parallel.
• It's hard to determine visually exactly at what position the best focus occurs.  If we could measure the intensity of the focused light as a function of distance behind the cylinder, perhaps by exposing photographic plates or using a tiny light sensor, we might obtain more accurate results. 
• Light travels not only through the substance filling the cylinder by through the substance of which the cylinder is made.  This substance in fact was different for the two substances observed (plastic in one case, glass in the other) and furthermore was of different thickness (the glass was thicker than the plastic).

Using trigonometry and the geometry of the circle, we determine that the distance d at which light focuses behind the cylinder is related to the radius R of the cylinder and the index of refraction n of the substance in the cylinder by the equation

• d = (2-n) / (2n-2) * R.

The analysis is accessible at the precalculus level but is reasonably involved.

Data obtained indicate that 

• For a water-filled cylinder of outer diameter 6.99  cm distance light focused at a point 6.5 cm from the central axis of the cylinder. 
• For a honey-filled cylinder of outer diameter 6.79 cm distanct light focused at a point 5.0 cm from the central axis of the cylinder.

It was assigned as a homework problem to find the index of refraction of the water and the honey.

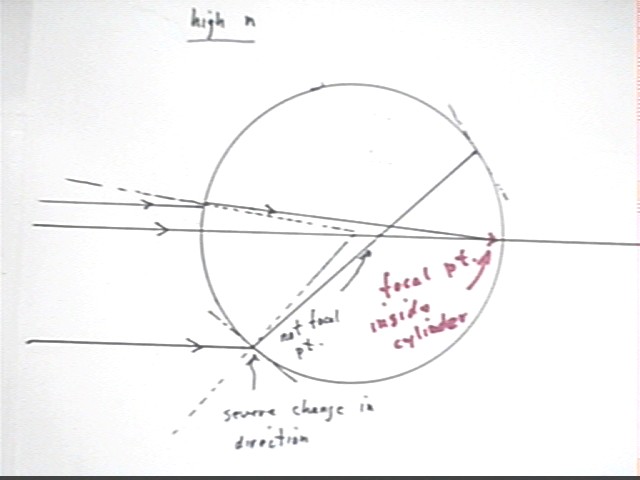
Note that for high index of refraction the focal point, indicated here by the position at which a beam initially parallel to the central beam intersects the central beam, will lie within the cylinder.

Note that for parallel beams further from the central beam the severe change in direction results in the beams not meeting at the focal point.  However for beams near the central axis the focal point will be valid.

• What is the maximum index of refraction that results in a focal point outside the cylinder?

Assignment 14:

• `gChapter 12 Problems 42, 46, 48, 52, 53 //

• `uUniversity Physics:  Ch. 21 Problems 23, 24, 26, 27, 30

Assignment 15:

• `gCh. 23 Problems 4, 11, 14, 17, 20//

• `uUniversity Physics:  Ch. 34, Problems 25, 28, 35, 40, 42//

Assignment 16:

• `gCh. 23 Problems 23, 34, 37, 43, 52//

• `uUniversity Physics:  Ch. 35, Problems 45, 52, 59, 62, 68, 75//

• `gCh. 23 Problems 58, 61; Ch. 24 Problems 4, 7, 10  Submit Ch. 24 #10//

• `uUniversity Physics:  Ch. 37, Problems 37, 40, 46, 49, 54  Submit Ch. 37 #44//

Assignment 18:

• `gCh. 24 Problems 15, 23, 28, 31, 34    //

• `uUniversity Physics:  Ch. 38, Problems 40, 45, 46, 49, 51//

Assignment 19:

• `gCh. 24 Problems 40, 43, 46, 51, 57, 60    Submit Ch. 24 #43//

Assignment 25:

• `gText Chapter 16, Problems 8, 11, 14, 18

• `uUniversity Physics:  Chapter 22 Problems 52, 54, 57, 60, 63, 66, 67, 74, 79, 83, 84

Assignment 26: 

• `gText Chapter 16, Problems 26, 29, 32, 35

• `uUniversity Physics:  Chapter 23 Problems 20, 21, 25, 27, 33, 34, 40, 41

Assignment 27: 

• `gText Chapter 17, Problems 9, 12, 16, 19, 22

• `uUniversity Physics:  Chapter 24 Problems 49, 50, 55, 57, 58, 61, 65, 72, 75

Assignment 28:    

• `gText Chapter 17, Problems 34, 37, 39, 45, 48

• `uUniversity Physics:  Chapter 25 Problems 36, 37, 42, 45, 46, 49, 52

Assignment 29: 

• `gText Chapter 18, Problems 6, 7, 9, 12, 29, 36    

• `uUniversity Physics:  Chapter 26 Problems 44, 47, 50, 55, 60, 61 

Assignment 30: 

• `gText Chapter 20, Problems 11, 13, 17, 21, 32    Submit #32//

• `uUniversity Physics:  Chapter 28 Problems 41, 42, 46, 52, 57, 65, 66; Chapter 29 Problems 43, 46, 51, 56

Assignment 31:    

• `gText Chapter 21, Problems 10, 12, 15, 22    

• `uUniversity Physics:  Chapter 30 Problems 31, 36, 41, 46