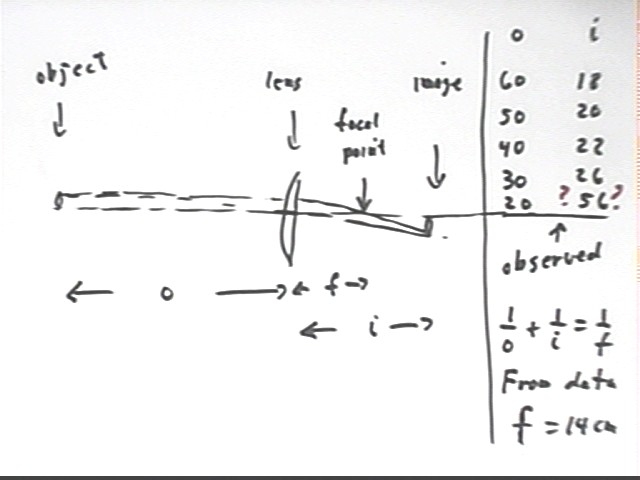
Observations of object and image distances for a lens are given below. Object and image distance are both calculated with respect to position of the lens.
Calculation of 1 / obj + 1 / img indicate that this quantity appears to be, within experimental error, constant.
The focal length, which is the reciprocal of the quantity 1 / obj + 1 / img, is the distance from the lens at which the image of an infinitely distant object will form. It is also the image distance at which a focused 'beam' is formed by the light from a point source.
The focal length for this lens, based on the results of these observations, appears to be about 14 cm.
The image formed by a distant object was observed at 14 cm from the lens, and a 'spotlight' beam was formed by a candle positioned at the focal distance in front of the lens.
| obj | img | 1/obj + 1/img | f=1/(1/obj+1/img) |
| 60 | 18 | 0.072222222 | 13.84615 |
| 50 | 20 | 0.07 | 14.28571 |
| 40 | 22 | 0.070454545 | 14.19355 |
| 30 | 26 | 0.071794872 | 13.92857 |

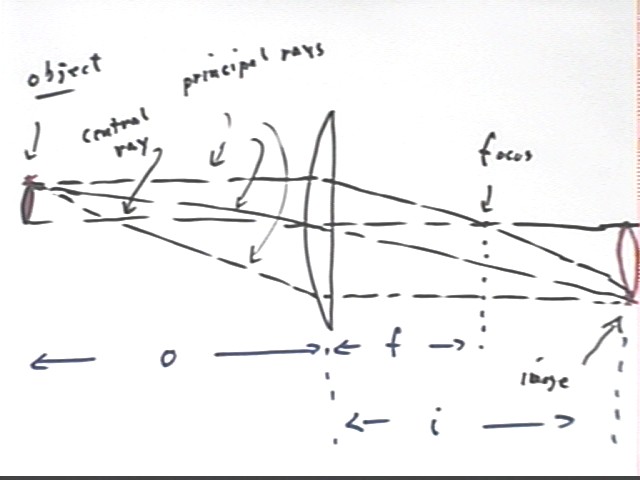
The figure below indicates how an image forms for a thin convex lens.
An object is positioned to the left of the lens. A 'central ray' extends from the base of the object through the center of the lens, along the central axis of the lens, and is undeflected. From the top of the object we sketch three 'principal rays', one parallel to the central axis, one passing thru the center of the lens, one emerging from the lens parallel to the central axis.
The first principal ray is parallel to the axis and hence is deflected to pass through the focus.
The second principal ray passes through the center of the lens and for a thin lens is undeflected.
The third principal ray passes through the central axis at a distance to the left of the lens which is equal to the focal distance. This ray will be deflected by the lens in such a way as to emerge parallel to the central axis.
All three principle rays meet at a point, which will be the image of the top of the object.
Other points on the object will also focus in the same vertical plane, forming a real image which can be viewed on a screen.
This image is inverted.
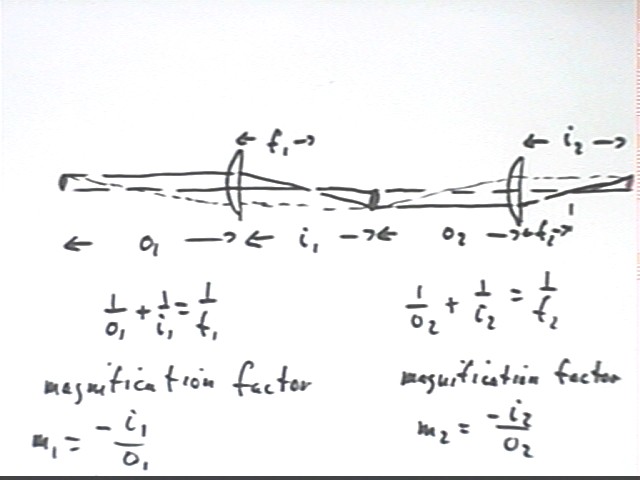
The figure below represents a real object at distance o1 to the left of a lens whose focal length is f1, which forms a real inverted image at distance i1 to the right of that lens.
This image serves as the object for a second lens, located at distance o2 from the image. The second lens has focal length f2 and forms an upright image of the original object at distance i2.
The distance i1 is easily calculated from f1 and o1. The magnification factor for this image is -i1 / o1.
The distance i2 is calculated from f2 and o2. The magnification factor for this image is -i2 / o2.
The first image is therefore -i1 / o1 times as large as the original object, and the second image is -i2 / o2 times as large as the first image, so that the second image must be -i1 / o1 * -i2 / o2 = i1 i2 / (o1 o2) times the size of the original object. Note that this is a positive multiple of the size of the original object, indicating that the image is upright.
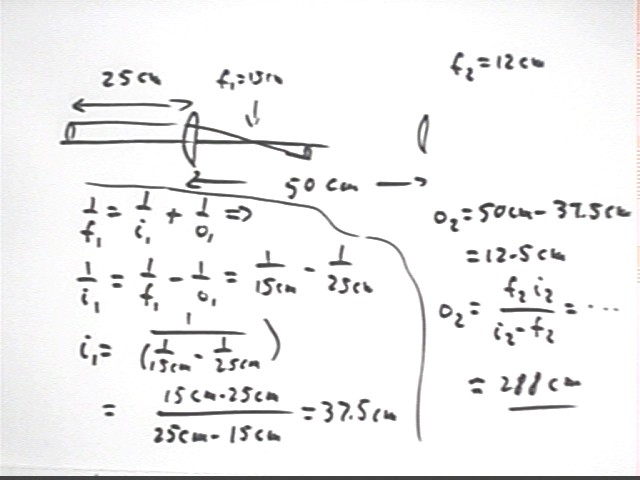
We calculate the distance of an image formed by two lenses, focal lengths 14 cm and 12 cm and separated by 50 cm, of an object lying 25 cm to the left of the first. This system is first set up and image distance and size are measured.
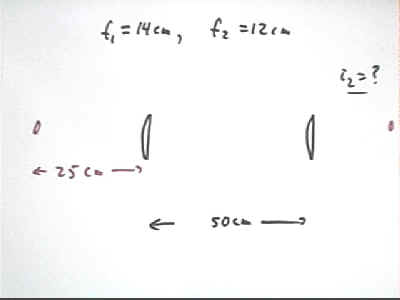
The image formed by the first lens is found below to lie 37.5 cm from that lens (see solution of the equation 1 / f1 = 1 / i1 + 1 / o1).
This image will therefore lie 50 cm - 37.5 cm = 12.5 cm from the second lens. Solving 1/f2 = 1 / i2 + 1 / o2 for o2 we obtain
o2 = f2 i2 / (i2 - f2) = ... = 288 cm. approx.
This is consistent with the distance measured for the real system.
The size of the first image will be -i1 / o1 = -37.5 cm / (50 cm) = -.75 times the size of the object, and the second image will be -i2 / o2 = -288 cm / 12.5 cm = -23 times the size of the first image. This makes it -.75 * 23 = 18 times as large as the original object, approximately.
This system, where the image formed by the first lens lies near the focal point of the second, forms a greatly magnified image.
Recall the gravitational force between two masses, which is an inverse-square force and is proportional to the product of the two masses.
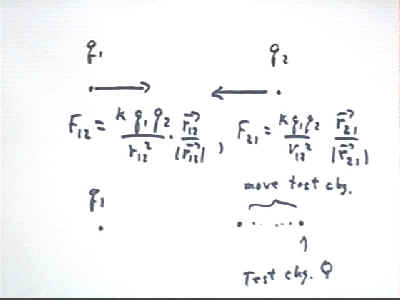
First note that the vector rAB from point A to point B has a magnitude equal to the distance from A to B, and is directed from point A toward point B. See the top of the figure below.
If we let m1 and m2 stand for two spherically symmetric masses, depicted in the figure below, then r12 and r21 stand respectively for the vectors from the center of mass 1 to the center of mass 2, and from the center of mass 2 to the center of mass 1.
The vectors r12/|r12| and r21/|r21|, each being a vector divided by its magnitude and hence having magnitude 1, are unit vectors directed respectively from the center of mass 1 toward the center of mass 2, and vice versa.
The magnitude of the force of attraction between these two masses is | F12 | = | F21 | = G m1 m2 / r^2, where r = r12 = r21 is the distance between the two points. Recall that the constant of proportionality is G = 6.7 * 10^-11 N m^2 / kg^2.
The force experienced by one of the masses is a vector whose magnitude is equal to G m1 m2 / r^2 and whose direction is that of the unit vector from that mass to the other, so that if F12 is the force exerted on mass 2 by mass 1, and F21 the force exerted on mass 1 by mass 2,
F12 = G m1 m2 / (r12)^2 * r12/|r12| and F21 = G m1 m2 / (r21)^2 * r21/|r21| .
These vectors are depicted in the lower half of the figure below, with the red unit vector in the same direction as the corresponding force vector.
If we consider two electrical charges q1 and q2 the force is given by an analogous inverse-square law, being proportional to the product of the two forces and inversely proportional to the distance between the forces. Unlike gravitational forces, electrostatic forces can be forces of attraction or repulsion, depending on whether the charges are like or unlike.
The constant of proportionality for the electrostatic force is k = 9 * 10^9 N m^2 / Coulomb^2, giving us F = k q1 q2 / r^2.
Specifically the forces F12 exerted by q1 on q2 and F21 exerted by q2 on q1 are given by
F12 = k q1 q2 / (r12)^2 * r12/|r12| and
F21 = k q1 q2 / (r21)^2 * r21/|r21| .
Note that these forces are in the form F = F * r / | r |, with F the product k q1 q2 / r^2, a positive or a negative number depending on whether q1 and q2 are of like or unlike sign, and r / |r| a unit vector in the direction of the force.
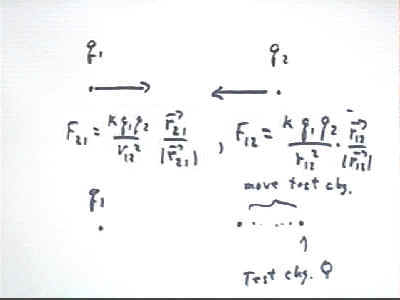
An important question is how much work is required to move a 'test charge' Q from one point to another in response to the force between this charge and a charge q1.
We note for now that if q1 is positive, then a positive test charge Q would be repelled by q1 and that positive work would therefore be required to move the test charge closer to q1.
It would follow that the work done per unit of test charge to move Q closer to q1 would be positive.
The electrostatic force is conservative: if we do positive work to move Q closer to q1, then if Q is released and allowed to move freely back to its original position the work we did will be returned in the form of increased KE.
Moving a positive test charge closer to q1 is therefore associated with an increase in the electrostatic potential energy of the charge.
The potential energy per unit of test charge is called the electrostatic potential. This quantity is analogous to the gravitational potential studied first semester.
Recall that, for example, the gravitational potential of a planet is the work per kilogram required to move a mass from a fixed reference position (e.g., the surface of the Earth) to a given position; between two given positions the change in gravitational potential is the work per kg required to move a mass from one position to another. Gravitational potential can be measured from any desired reference position; infinite separation from a planet is the standard reference position though other positions (e.g., the surface of the planet as mentioned above) can also be used.
The electrostatic potential tends to change from point to point. The change in potential energy per unit of test charge is the change in electrostatic potential, and will be measured in units called volts.
A volt is a Joule per Coulomb, abbreviated J / C. Remember that change in potential is a measure of the work per unit of charge, with standard unit J / C, between two points.