At the points (10 cm, 10 cm), (10 cm, 0 cm) and (0 cm, 10 cm) what is the magnitude and direction of the electric field due to a charge of 1 microCoulomb located at the origin?
We figure out the force that would be exerted on a 1 Coulomb test charge at each point.
At (10 cm, 0) the force would be
k q1 q2 / r^2 =
9 * 10^9 N m^2 / C^2 * 10^-6 C * 1 C / (.10 m)^2 =
9 * 10^9 N m^2 / C^2 * 10^-6 C^2 / (.01 m^2) =
9 * 10^5 N.
Since this force is based on a 1 C test charge, the electric field at this point is therefore 9 * 10^5 N / C.
The force and the field will be directed away from the origin, along the positive x axis.

At (10 cm, 10 cm) the distance from the charge at the origin is
r = sqrt((.1 m)^2 + (.1 m)^2) = sqrt(.02 m^2) = .14 m, approx.
Note that we're going to want to use r^2, which we can see is .02 m^2, so we don't need to bother with the approximation r = .14 m.
The force at this point is
F = k q1 q2 / r^2 =
9 * 10^9 N m^2 / C^2 * 10^-6 C + 1 C / (.02 m^2) =
4.5 * 10^9 N.
Since this force is based on a 1 C test charge, the electric field at this point is therefore 4.5 * 10^5 N / C.
The force and the field will be directed away from the origin, at an angle of 45 degrees.

At (0, 10 cm) the field will be 9 * 10^5 N / C, just as it was at (10 cm, 0), but will be directed along the positive y axis.
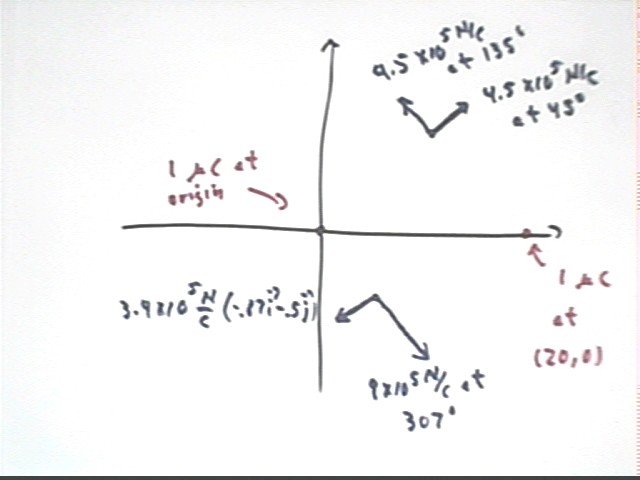
These fields are plotted in the figure below.
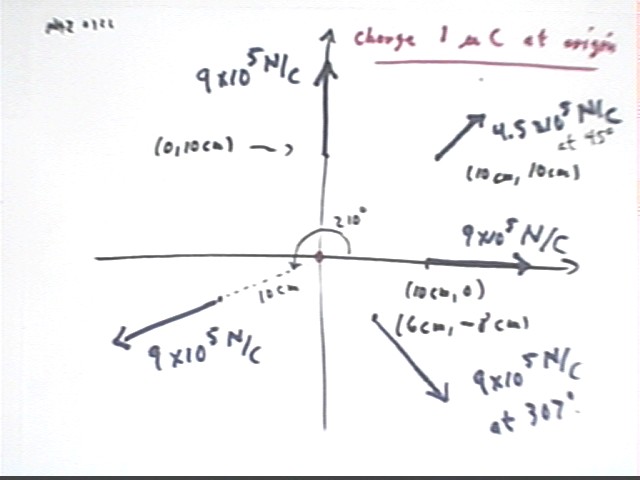
The field is also depicted at two other points.
The first is the field at a position 10 cm from the origin, with displacement at 210 deg from the positive x axis.
Since this point is 10 cm from the origin the magnitude of this field is the same as the magnitude of any other field at the 10 cm distance, or 9 * 10^5 N/C.
The direction of this field is directly away from the origin, at 210 deg from the positive x axis. Note that the x and y components of this force could easily be calculated.
The second is at position (6 cm, -8 cm).
The Pythagorean Theorem shows us that this point is 10 cm from the origin, so the magnitude of the force will again be 9 * 10^5 N / C.
The direction of the force is parallel to a vector from the origin to (6 cm, -8 cm), which has direction arctan(-8 cm / (6 cm) ) = -53 deg or 360 deg - 53 deg = 307 deg.
This information will make it easy to calculate the components of this vector, should we require this information.

To illustrate the use of unit vectors i and j, the calculation of the direction of the field at (6 cm, -8 cm) is repeated below in terms of the unit vectors i and j , unit vectors respectively in the positive x and the positive y directions, as depicted below.
The displacement vector from the origin to (6 cm, -8 cm) is r = 6 i + (-8 j ) = 6 i - 8 j , where the unit cm is understood.
The magnitude of this vector is | r | = | 6 i - 8 j | = sqrt(6^2 + (-8)^2) | = 10.
The angular direction of this vector is arctan ( y component / x component) = arctan ( j component / i component) = arctan( 6 / (-8) ) = -53 deg, or 360 deg - 53 deg = 307 deg.

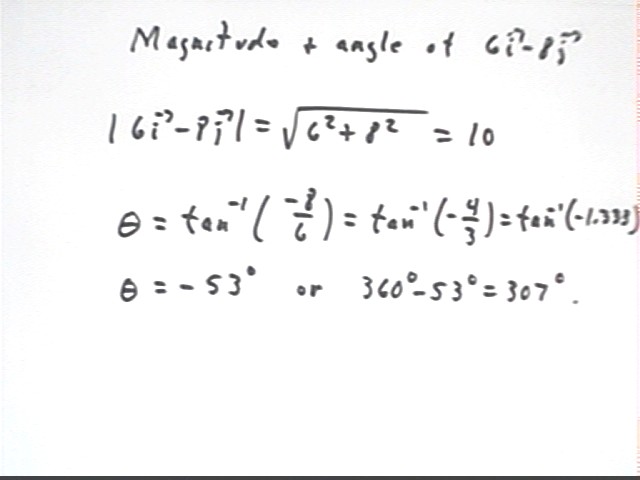
Find the field at the same points due to a charge of 1 microCoulomb at (20 cm, 0).
From (20 cm, 0) to (10 cm, 10 cm) the displacement vector is r = -10 i + 10 j with magnitude r = sqrt( (.1 m)^2 + (.1 m)^2 ) = sqrt(.02 m^2) and angle arctan(10 / (-10) ) + 180 deg = -45 deg + 180 deg = 135 deg. Note that the 180 deg is added because the x component of the vector is negative.
The force at this point is therefore 4.5 * 10^5 N directed parallel to r at 135 deg.
Since this force results from a 1 C test charge the field at this point is 4.5 * 10^5 N / C are 135 deg.
A unit vector in the direction of r is r / | r | = (-10 i + 10 j) / | -10 i + 10 j | = .71 i + .71 j .
We can easily write the field in terms of this unit vector as magnitude * unit vector in direction of field:
E = 9 * 10^5 N/ C * (.71 i + .71 j ).
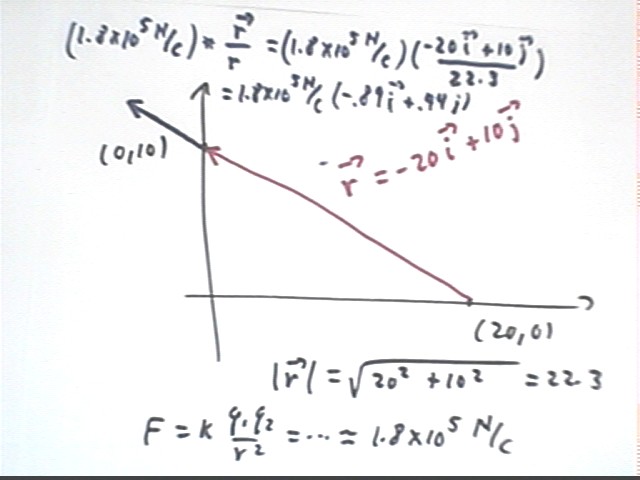
At (0 cm, 10 cm) the displacement vector is r = -.20 m * i + 10 m * j with magnitude r = sqrt( (.2 m)^2 + (.1 m)^2 ) = sqrt(.05 m^2).
This results in a force of 1.8 * 10^5 N directed parallel to r.
The unit vector in the direction of r is r / | r | = (-.20 m i + .10 m j) / sqrt(.05 m^2) = -.90 i + .45 j .
In the figure below the unit vector is calculated based on the -20 cm and 10 cm displacements, without being converted to meters. You should verify that it makes no difference in the final result for the unit vector.
The field at this point is therefore
E = 1.8 * 10^5 N/ C * (-.90 i + .45 j )
(note that due to a slight error in mental calculation the unit vector is erroneously written in the figure as (-.89 i + .44 j )).
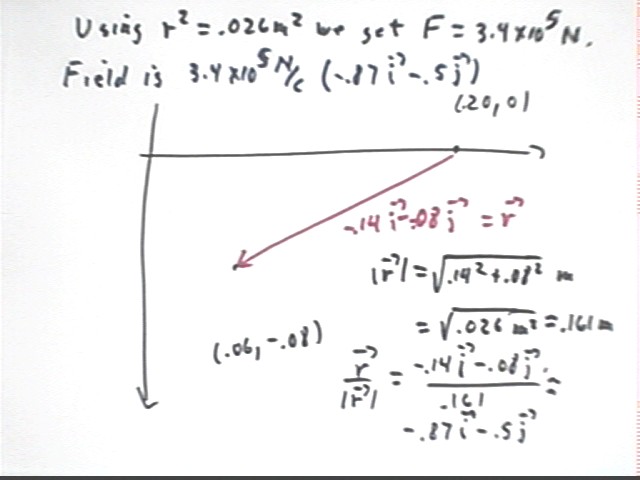
From (20 cm, 0) to (6 cm, -8 cm) the displacement vector is r = -.14 m i - .08 m j , with magnitude r = sqrt( (.14 m)^2 + (.08 m)^2 ) = sqrt(.026 m^2) = .161, approx.. A unit vector in the direction of r is r / | r | = (-14 i + 8 j) / | (-14)^2 i + (-8)^2 j | = -.87 i - .50 j . The angle at which this vector is directed is arctan(-.08 / (-.14) ) + 180 deg. Note that the 180 deg is added because the x component of the vector is negative.
The force at this point found as in preceding examples, using r^2 = .026. The result is force F = 3.4 * 10^5 N, field 3.4 * 10^5 N / C in the direction of the unit vector.
We can easily write the field in terms of this unit vector as magnitude * unit vector in direction of field:
E = 3.4 * 10^5 N/ C * (-.87 i - .50 j ).
The vectors we have calculated here in response to the 1 microCoulomb charge at (20 cm, 0) are depicted in the figure below.
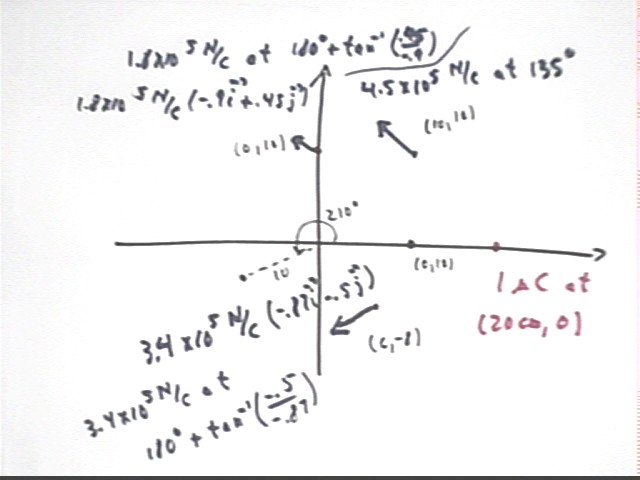
If we now superpose at the point (10 cm, 10 cm) the fields due to the two point charges, each 1 microCoulomb, one at the origin and the other at (20 cm, 0) we obtain the fields indicated in the figure below at that point.
The resultant of the two fields is easily obtained be standard vector methods from the magnitudes and directions of the two fields (i.e., find the components, find the sum of the components in each direction, use Pythagorean Theorem and arctan to get the magnitude and direction of the resultant). You should calculate this resultant yourself.
You should get something like 6.3 * 10^5 N / C at 90 deg (i.e., vertically upward).
The two fields at (6 cm, -8 cm) are also depicted in the figure below. You should calculate the resultant of these two vectors. Note that you can simply multiply the 3.4 * 10^5 N/C vector by the unit vector to get its components. You'll have to use sines and cosines to get the components of the other vector.
You should be able see in these calculations how all the vectors in the three figures below, repeated from notes from the preceding class, can be calculated.