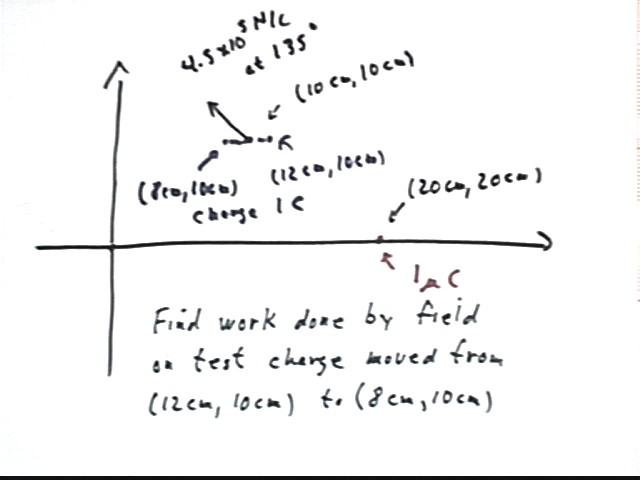
The field at the (10 cm, 10 cm) point of the field of charge 1 microCoulomb at (20 cm, 0) was 4.5 * 10^5 N/C at 135 deg.
We wish to find the work necessary to move a test charge of 1 Coulomb through this field, with the test charge moving from the point (12 cm, 10 cm) to (8 cm, 10 cm), a horizontal displacement of 4 cm to the left.

The figure below shows this field vector and the two points, now labeled A and B.
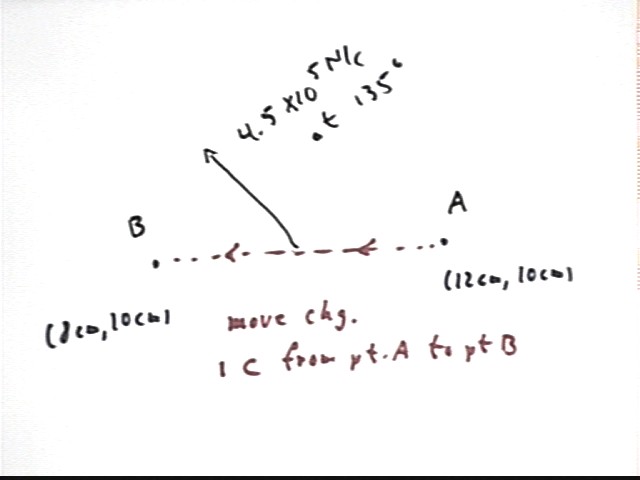
The electric field between A and B varies a bit. It is closer to vertical at A than at the point (10 cm, 10 cm) in the middle of the segment, and closer to horizontal at B. SInce A is closer to the source charge at (20 cm, 0), the magnitude of the field at A is also somewhat greater than the field at B.
The variations in the field over the path from A to B are not totally insignificant, but if we use the 'midpoint' field 4.5 * 10^5 N/C directed at 135 deg we will obtain a good approximation to the work.

The force exerted by the field on a 1 C test charge is 4.5 * 10^5 N, directed at 135 deg. We easily see that this force has components

The displacement `ds from A to B has components `dsx = -4 cm and `dsy = 0.
The work done in moving the charge from A to B is the sum of Fx `dsx and Fy `dsy:
Since this work was done on a 1 C test charge, the work done by the field per unit of charge from A to B is 1.3 * 10^4 J / C, or 1.3 * 10^4 volts. Thus the potential difference from A to B is Vab = 1.3 * 10^4 volts = 13,000 volts.

We can prove using calculus that the electric field is conservative, which means that we can 'get back' the work done against the field between two points if we allow it to return to its original point.
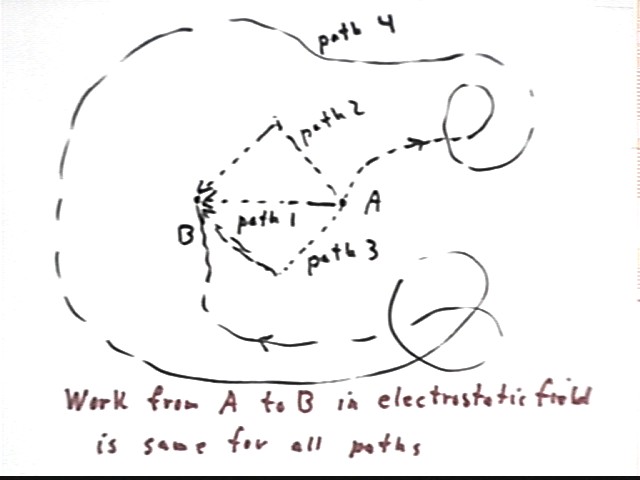
This is equivalent to saying that it doesn't matter what path you take, the work done against the field is the same for any path that connects two given points. In this case it means that the work done from A to B is independent of the path, and the work done would have been the same had we followed any of the paths shown in the figure below, or any other path from A to B.
You might want to verify this for path 2, which runs at 135 degrees for distance 4 sqrt(2) / 2 cm then at 225 degrees for the same distance. For the first part of the path we note that the path is parallel to the field so that the work is just force * displacement, and for the second part it is perpendicular to the field so that the work is zero. The product of 4.5 * 10^5 N and 4 sqrt(2) cm is the same as the result we obtained in the preceding figure. You can also find `dsx and `dsy, and hence Fx `dsx * Fy `dsy for each part of the path; the sum is again equal to the preceding result and the calculations for the two parts of the path are instructive.
In general if we move a test charge qTest from point A to point B parallel to an electric field E we find the following:
The units of these quantities help us understand these relationships. Force (in N) is the product of the field (in N / C) and the test charge (in C). That is, N / C * C = N.
The work done is the product of the force (in N) and displacement (in m), giving us work in N m or Joules.
The potential difference is work per unit of test charge, in J / C.

Using a battery or a generator of sufficient capacity it is possible to create a potential difference, or voltage, between two points. You have experienced this with your generator.
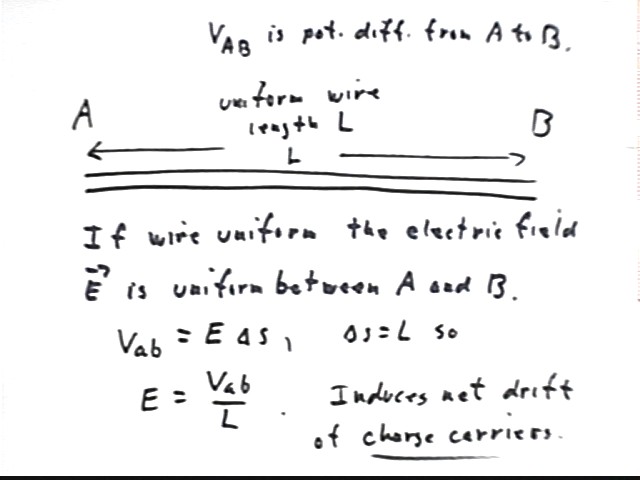
For reasons we will see later the electric field in a uniform wire for which the only source of potential difference runs from point A to point B is very nearly uniform over the length and cross-section of the wire, and this field is at all points very nearly parallel to the wire.
Since the potential difference of a uniform field over a displacement in the direction of the field is V = E * `ds, we see that for this wire the field is
In a conducting wire there are numerous free charge carriers (usually electrons; not that in semiconductors we can have what amount to migrating positive charges, and in ionized gases both positive and negative ions can migrate).
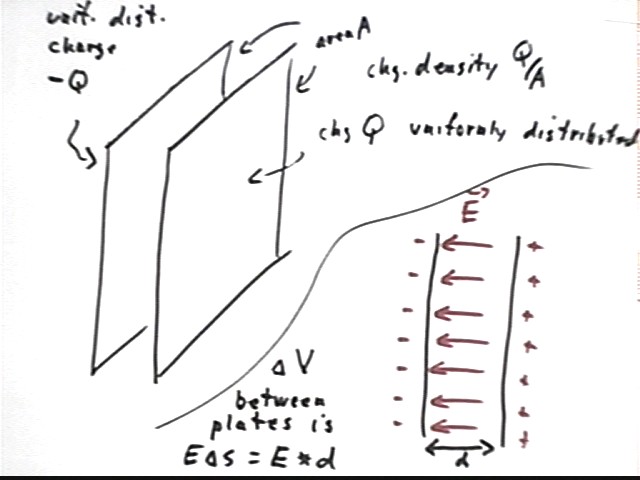
If we have two initially uncharged parallel plates separated by a distance which is short compared to their dimensions, and if we 'rob' one of charge Q and placte that charge on the other, then there will be a net charge of -Q the plate from which charge Q was removed, and of course net charge Q on the other plate.
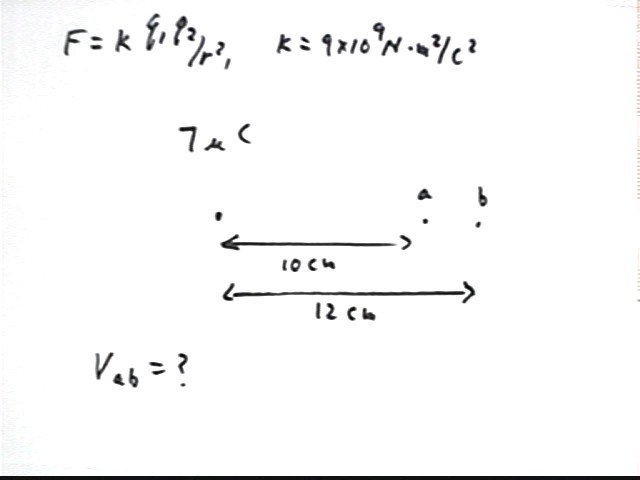
What is the potential difference from point a, lying 10 cm from a 7 microCoulomb charge, to point b lying 12 cm from that charge?
Moving from pt A at (12 cm, 10 cm) to pt B at (8 cm, 10 cm), a 1 C test charge in the field of the 1 microCoulomb charge at (20 cm, 0) will:
experience a variable force which averages close to 4.5 * 10^5 N directed at 135 deg
will have work Wab = Fx `dsX + Fy `dsY = 1.3 * 10^4 J done on it by the field.
The work done by the charge against the field is therefore -1.3 * 10^4 J.
The work done by the charge, per unit of charge, is therefore -1.3 * 10^4 J / C.
Thus the PE of the charge changes by -1.3 * 10^4 J, and the PE change per unit of charge is -1.3 * 10^4 J / C.
PE change per unit of charge in an electric field is called change in electrostatic potential, or change in voltage, where a volt is a Joule per Coulomb.
The potential difference from A to B is therefore -1.3 * 10^4 J / C = -1.3 * 10^4 volts.
The work done from point A to point B is independent of the path taken from A to B. We can therefore speak of the potential difference from A to B without worrying about which path we take.
This implies that any work we do to move a charge from one point to another is 'stored' as PE, and can be recovered in the form of work or KE as the particle moves back from point B to point A.
The process we used to find Vab was the following:
Multiply electric field E by test charge q to find force.
Multiply force parallel to displacement by displacement to get work.
Divide the work by the test charge to get the work per unit charge, which we called potential difference or voltage.
In symbols:
F = qTest * E
F * `ds = Wab
Vab = Wab / qTest
If we put all this together we see that
Vab = Wab / qTest = F * `ds / qTest = qTest * E * `ds / qTest = E * `ds, or just
Vab = E * `ds.
******* old stuff??? ****
We can use things like batteries and turbines to create potential differences between points.
...
For the field of a single charge of 7 microCoulombs, find the potential difference between point a lying 10 cm from the charge and point b lying 12 cm from the charge.
We will assume a 1 C test charge, moved from a to b.
Since potential difference is independent of path we might as well assume the charge and these point to lie on the same straight line.
At a distance of 10 cm the force on the test charge is k q1 q2 / r^2 = 9 * 10^9 N m^2/C^2 * 7 * 10^-6 C * 1 C / (.1 m)^2 = 6.3 * 10^6 N.
At distance 12 cm the force on the test charge is similarly found to be about 4.5 * 10^6 N.
The average force on the test charge is therefore approximately
ave force = (6.3 * 10^6 N + 4.5 * 10^6 N) / 2 = 5.4 * 10^6 N.
The field is directed away from the positive 7 microCoulomb charge, in the direction from a toward b. The work done by the field in moving the test charge from a to b is therefore
work by field = 5.4 * 10^6 N * .02 m = 1.1 * 10^5 Joules, approx.
The work done by the test charge against the field, which is the change in the PE of the test charge, is therefore
work done by test charge against field = - work by field = -1.1 * 10^5 Joules.
The potential difference between a and b is therefore
Vab = work per unit charge against field = -1.1 * 10^5 J / C, or -110,000 volts, approx..
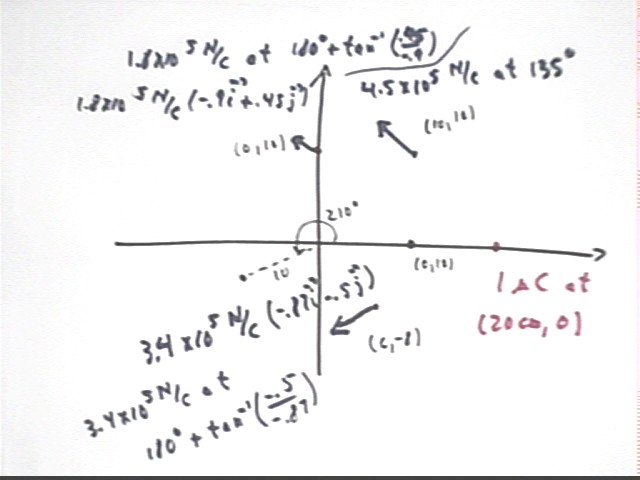
At the points (10 cm, 10 cm), (10 cm, 0 cm) and (0 cm, 10 cm) what is the magnitude and direction of the electric field due to a charge of 1 microCoulomb located at the origin?
We figure out the force that would be exerted on a 1 Coulomb test charge at each point.
At (10 cm, 0) the force would be
k q1 q2 / r^2 =
9 * 10^9 N m^2 / C^2 * 10^-6 C * 1 C / (.10 m)^2 =
9 * 10^9 N m^2 / C^2 * 10^-6 C^2 / (.01 m^2) =
9 * 10^5 N.
Since this force is based on a 1 C test charge, the electric field at this point is therefore 9 * 10^5 N / C.
The force and the field will be directed away from the origin, along the positive x axis.
At (10 cm, 10 cm) the distance from the charge at the origin is
r = sqrt((.1 m)^2 + (.1 m)^2) = sqrt(.02 m^2) = .14 m, approx.
Note that we're going to want to use r^2, which we can see is .02 m^2, so we don't need to bother with the approximation r = .14 m.
The force at this point is
F = k q1 q2 / r^2 =
9 * 10^9 N m^2 / C^2 * 10^-6 C + 1 C / (.02 m^2) =
4.5 * 10^9 N.
Since this force is based on a 1 C test charge, the electric field at this point is therefore 4.5 * 10^5 N / C.
The force and the field will be directed away from the origin, at an angle of 45 degrees.
At (0, 10 cm) the field will be 9 * 10^5 N / C, just as it was at (10 cm, 0), but will be directed along the positive y axis.
Find the field at the same points for due to a charge of 1 microCoulomb at (20 cm, 0).
At (10 cm, 10 cm) the displacement vector is r = -10 i + 10 j with magnitude r = sqrt( (.1 m)^2 + (.1 m)^2 ) = sqrt(.02 m^2).
This results in a force of 4.5 * 10^5 N directed parallel to r at 135 deg.
At (0 cm, 10 cm) the displacement vector is r = -20 i + 10 j with magnitude r = sqrt( (.2 m)^2 + (.1 m)^2 ) = sqrt(.05 m^2).
This results in a force of 1.8 * 10^5 N directed parallel to r.
The unit vector in the direction of r is r / | r \ = -.20 m i + .10 m j / sqrt(.05 m^2) = -.9 i + .45 j .