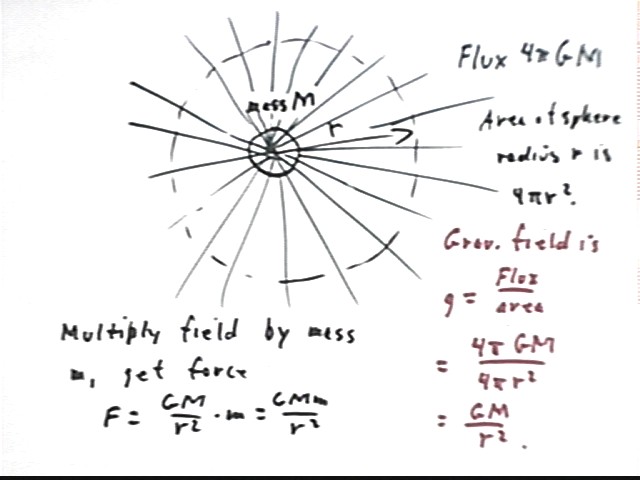
Gauss' Law
Recall: Gravitational flux of a mass M is 4 pi G M, with G = 6.7 * 10^-11 N m^2 / kg^2. What is the gravitational flux of a mass of 4 * 10^23 kg?
The gravitational flux is 4 pi G M = 4 pi * 6.7*10^-11 N m^2 / kg^2 * 4 * 10^23 kg = 1.07 * 10^14 pi N m^2 / kg.

If we sketch a sphere of radius 10,000 km about this mass and concentric with the mass then what angle do the field lines make with the surface at a given point on the surface? Assume that the radius of the planet is less than 10,000 km, so that this sphere completely contains the mass of the planet.
The field lines run parallel to the gravitational field, which is always directed toward the center of the planet. The field line therefore run radially toward the center of the planet. Radial lines running toward or away from the center of a sphere are perpendicular to the surface of the sphere, so the lines pass through the surface perpendicular to that surface.
What is the flux per unit area
The total flux is 1.07 * 10^14 pi N m^2 / kg. The area of the sphere is 4 pi r^2 = 4 pi * (10,000,000 m)^2 = 4 * 10^14 pi m^2.
The flux per unit area is therefore
flux / area = 1.07 * 10^14 pi N m^2 / kg / (4 * 10^14 pi m^2) = .27 N / kg = .27 m/s^2.
Note that the units of flux / area are the units of acceleration, which is the unit of a gravitational field.
What expression gives us the gravitational flux density, which is flux per unit area, due to mass M at distance r from the mass?
Flux density over a sphere of radius r is the gravitational field strength g at that point:
g = flux / surface area = 4 pi G M / (4 pi r^2) = G M / r^2.
This expression is identical to the expression for the gravitational field of a spherically symmetric mass M at a distance r > radius of mass.
We can apply a completely analogous model to the electrostatic flux of a point charge q passing through a surface which contains that charge. The total flux is 4 pi k q and if the shape of the surface is such that the electric field is of uniform magnitude everywhere on the surface and passes at a perpendicular through the surface at every point, then the electric field is just
E = flux / area.
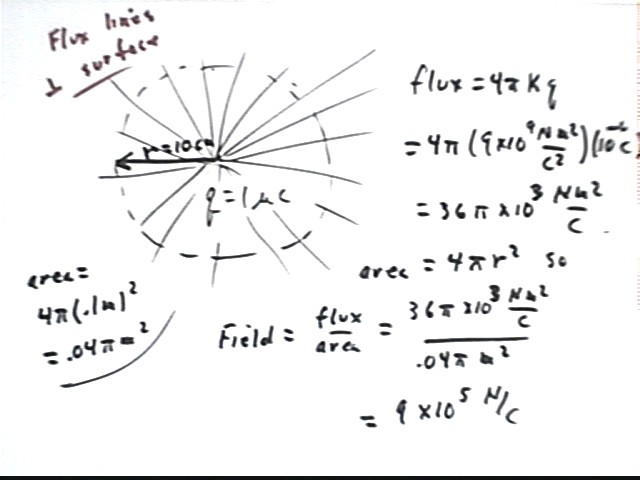
What therefore is the flux, surface area and field for a sphere of radius 10 cm containing at its center a charge q = 1 microCoulomb?

The total flux of the charge is 4 pi k q = 36 pi * 10^3 N m^2 / C.
The area of the surface is 4 pi r^2 = 4 pi ( .1 m )^2 = .04 pi m^2.
The electric field does extend radially from the charge and hence passes through the surface at a perpendicular. The symmetry of the situation ensures that the magnitude of the charge is the same at every point of the sphere (if it wasn't then we could rotate the coordinate system and change the field at some points). So the criteria are met and we can say that
E = flux / area = 36 pi * 10^3 N m^2 / C / (.04 pi m^2) = 9 * 10^5 N / C.
Note that this result has been obtained several times for the field of a 1 microCoulomb charge at a point 10 cm from the charge.
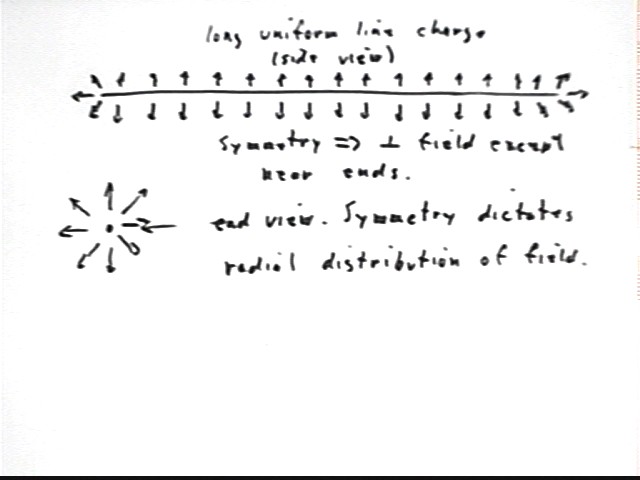
Now consider a thin straight conducting wire 100 m long. 12 microCoulombs of charge are distributed along the wire. Since the wire is a conductor these charges are free to move wherever they will. Since the individual charges that make up the 12 microCoulombs repel each other very strongly, they will get as far away from one another as possible. This puts them on the surface of the wire, equally distributed along its length.
At points near the wire what will be the direction of the electric field?
If we look at the wire from the side, assuming a horizontal orientation, we first account for the fact that the charge distribution will be the unchanged if we reverse the wire. The result is that the field will be symmetric about a vertical axis thru its center.
We next note that due to the inverse-square nature of the electrostatic force the field at a given point will be mostly due to the points on the wire which are closest, and will be influenced very weakly by points lying far away in comparison to the distance from the point to the wire. Since nearby points to the right and to the left have equal effect but in the opposite horizontal direction it follows that unless the point is close to the end of the wire the field will be very nearly perpendicular to the wire.
Near the ends the absence of wire on one side will result in a field that points away from the wire, more and more so as we get closer to the ends. The top of the figure below sketches the resulting field in a vertical plane.
An end view of the wire shows that due to rotational symmetry the field must be uniform at a given distance and radial in its direction. Otherwise rotation would change the field at some points.
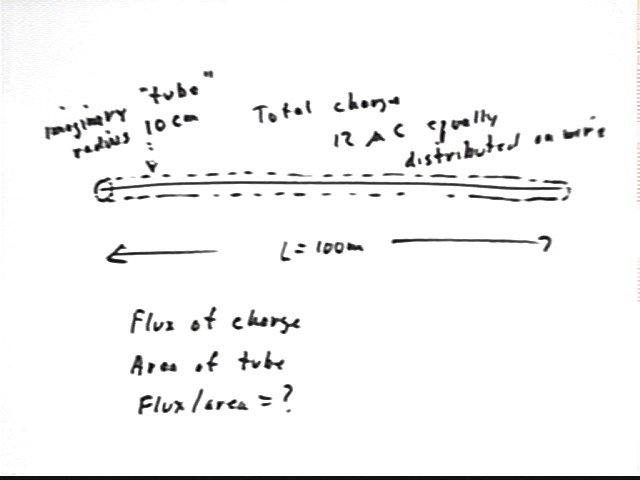
If we construct an imaginary cylindrical 'tube' of radius 10 cm, with the wire at its central axis, is the electric field constant, or nearly so, along the curved sides of the tube and does it pass through this tube at a perpendicular?
Since the field is radial and very nearly perpendicular to the wire along nearly the entire length of the wire this is pretty much the case. There are slight discrepancies with this behavior near the ends, but since the tube is only 10 cm from the wire and the wire is 1000 times this long almost all points of the tube experience a very nearly perpendicular flux.
What is the total flux through the tube?
The tube contains charge 12 microCoulombs so the flux is 4 pi k q = 4 pi * 9 * 10^9 N m^2 / C^2 * 12 * 10^-6 C = 4.32 * 10^5 pi N m^2 / C.
What is the area of curved surface of the tube?
The area of the 'tube' is circumference * length = (2 pi r) * length = (2 pi * .1 m) * 100 m = 20 pi m^2.
If we ignore the small amount of flux through the ends of the tube and the slight variations in the perpendicular nature of the field near the ends, what is the electric field at the curved surface of the tube?
The field is flux / area = 4.32 * 10^5 pi N m^2 / C / (20 pi m^2) = 2.16 * 10^4 N / C.
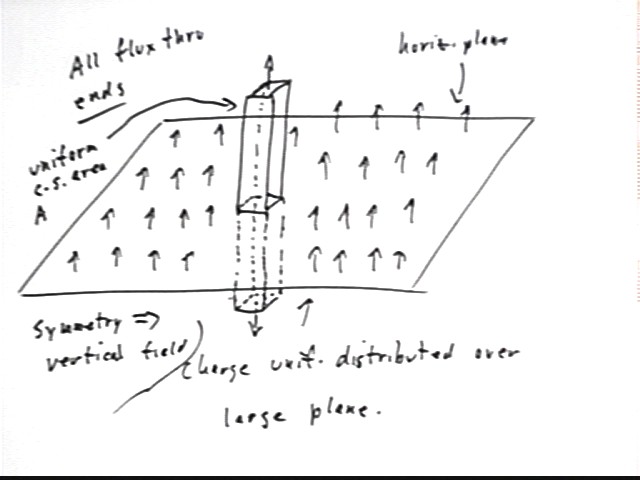
What is the direction of the electric field at a point near an extensive uniform horizontal plane distribution of positive charge, at a point not near the edges of the plane?
Since the point is much nearer the plane than the edges of the distribution, and since the field contribution of distant points falls off as the square of the distance, it will turn out that even though there is a lot more plane at great distances the net effect of distant parts falls off with the distance and only relatively nearby charge makes a contribution. The charge out to any given distance is distributed the same in all horizontal directions, so the horizontal contributions of all charges within that given distance cancel one another and leave only a vertical field at the point.
So for any point near the horizontal plane distribution the field will be directly away from the plane, i.e., perpendicular to the plane.
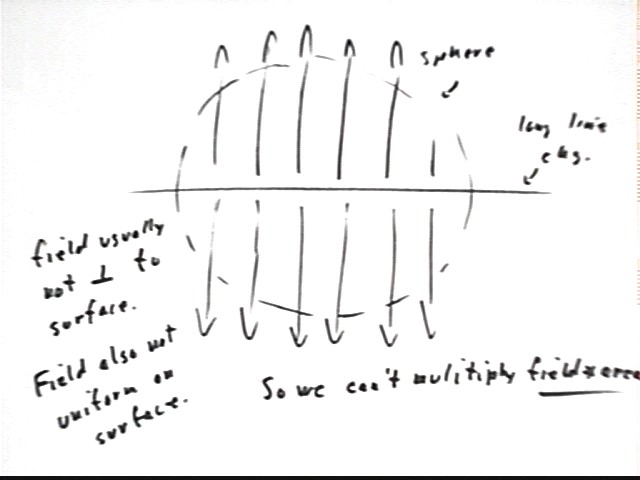
If we construct a spherical surface with its center on the plane charge distribution, with the edges much more distant than the plane from every point on the sphere, then will the field pass through every point of the sphere at a perpendicular to the sphere? Can we use this sphere to calculate the electric field using the flux model?
The field is always perpendicular to the plane. The sphere is not always perpendicular to the plane so the field will not pass through every point of the sphere at a perpendicular. This is depicted in the figure below.
We cannot use the flux model with this sphere to calculate the electric field, since the field does not pass through the sphere at a perpendicular.
If we construct a rectangular 'box', with all its points much nearer the plane than the edges, with the box passing through the plane and with its sides perpendicular to, and its top and bottom parallel to the plane, do any flux lines exit through the sides of the box?
The flux lines are perpendicular to the plane, as are the sides of the box. So the flux lines are parallel to the sides. If a flux line is 'in' the side of the box it will stay there until it gets through the top or bottom, and will therefore exit only through the top or bottom. If a flux line is not already 'in' the side it will remain parallel to the side and never enter or leave it.
The flux lines go on forever so they must exit the box. Where do they exit the box, and do they exit perpendicular to the surface at the exit point?
The flux lines exit at the top and bottom of the box. The top and bottom are parallel to the plane and the field lines are perpendicular to the plane, so the field lines are perpendicular to the top and bottom of the box. They do therefore exit at a perpendicular to the surface from which then exit.
If an extensive horizontal distribution is characterized by charge density 40 microCoulombs / m^2, then how much charge is contained on a rectangular region 3 meters by 2 meters, and what is the flux of that charge?
This region has area 3 m * 2 m = 6 m^2, and so contains 40 microCoulombs / m^2 * 6 m^2 = 240 microCoulombs of charge. The flux of this charge is
flux = 4 pi k q = 4 pi * 9 * 10^9 N m^2 / C^s * 240 microCoulombs = 8.64 * 10^6 pi N / m^s.
Through how much area does this flux exit and what therefore is the electric field at the exit points?
The flux exits through the top and bottom of the box, which have total area 12 m^2.
The field is therefore flux / area = 8.64 * 10^6 pi N m^2 / C / (12 m^2) = 2.2 * 10^6 N / C.

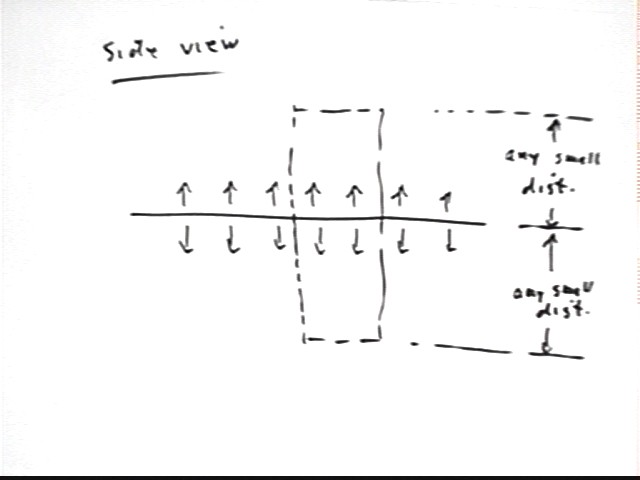
Did any of this analysis assume an particular height for the box, other than assuming that the box never gets too far from the charge plane?
No such assumption was made.
What does this tell us about the relationship of field strength to distance from the plane?
As long as we are much closer to the plane than to any of its edges the field strength does not depend on distance. The field of a uniform plane charge distribution, near the plane, is independent of just how near.
The figure below provides a side view of the situation. The distances of the top and the bottom of the box from the plane do not matter at all, and do not have to be equal, as long as these distances are much closer to the plane than to its edges.
As long as the field is perpendicular to the plane, the flux must exit only through top and bottom, and at a perpendicular.
Wires that Narrow (-> series circuits)
Wires that Branch (-> parallel circuits)
Potential Energy Change around a Loop (Kirchoff's #? law)
Parallel-Plate Capacitors
Discharge of a Parallel-Plate Capacitor
Cylindrical Capacitors