Gauss'
Law
Using
symbols, what is the flux of a point charge q at the center of an imaginary
sphere of radius r?
The
flux is 4 pi k q.
Using
symbols, what is the surface area of the surrounding sphere?
The
sphere’s area is 4 pi r^2.
Symmetry
arguments prove that the field is uniform at the surface of the sphere and at
every point perpendicular to the surface so what is the electric field at the
surface of the sphere?
The
field is E = flux / area = 4 pi k q / 4 pi r^2 = k q / r^2.
This
is consistent with Coulomb’s law, since the force on a test charge Q at this
point will be
·
Force = Q E = Q * k q / r^2 = k q Q / r^2.
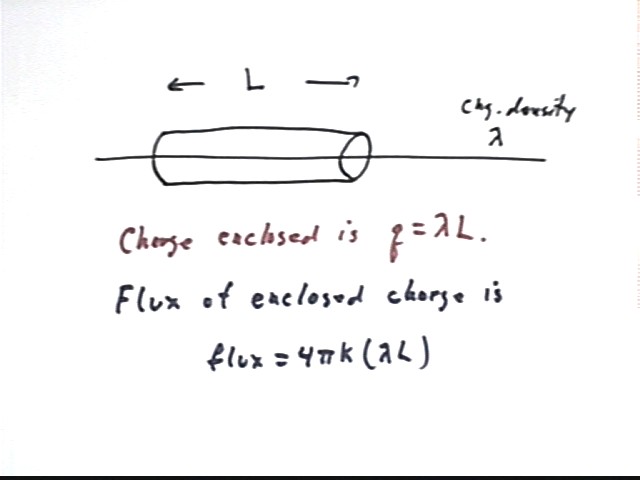
If
we have a long line of uniformly distributed charge with charge density lambda
(measured in charge / unit length) then how much charge is enclosed in a
cylinder of length L and radius r which surrounds the wire?
What is the flux of this charge?
The
cylinder encloses charge q = lambda * L (charge / length * length).
The flux of the charge is therefore
·
Flux = 4 pi k q = 4 pi k (lambda L)
If
the line charge coincides with the axis of the cylinder then do the conditions
for Gauss’ Law hold?
By
symmetry arguments the electric field is of constant magnitude and radial, so it
is everywhere uniform in magnitude perpendicular to the curved surface of the
cylinder.
So
what is the magnitude of the field at the curved surface?
The
area of the curved surface is circumference * length = 2 pi r * L
·
E = flux / area = 4 pi k lambda L / (2 pi r L) = 2 k lambda / r.
Note
that this is an inverse first power, as opposed to the inverse square of a point
charge.
Note also that there is no flux through the ends of the cylinder, since the ends are parallel to the field.

What
is the charge enclosed within an area A of an infinity plane distribution of
charge having uniform charge density sigma (measured in charge / unit area)?
What is the flux of this charge?
The
charge enclosed is sigma * A. The
flux is 4 pi k ( sigma * A).
If
we construct a rectangular box with sides perpendicular to the plane, with the
top of the box above and the bottom of the box below the plane, and with
cross-sectional area A then what is the electric field at the top and at the
bottom?
The
flux exits thru top and bottom, total area 2 A, so the field is
·
E = 4 pi k sigma A / (2 A) = 2 pi k sigma.
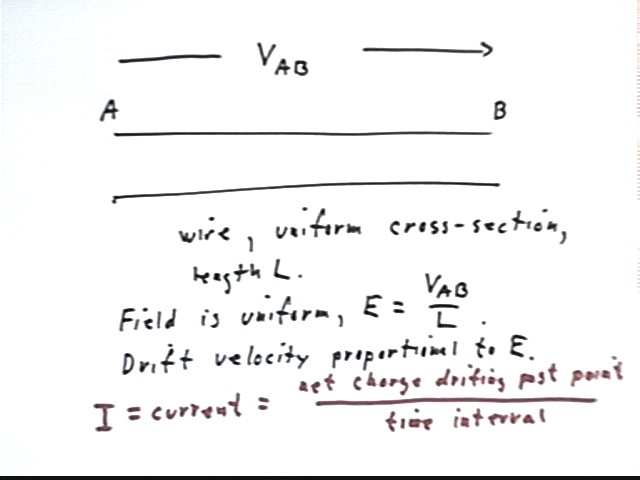
What is the electrical field in a uniform wire of length L across which a potential difference Vab is maintained? How does this field affect the drift velocity of charge carriers?
The field is E = Vab / L.
Greater field implies greater acceleration of charge carriers between collisions.
In most cases frequency of collisions is not significantly affected by drift velocity, which is generally very much less than thermal velocity.
This results in proportionally greater velocity change between collisions.
The average drift velocity is therefore very nearly proportional to the electric field.
Note that current is defined as the time rate of charge drift past a point:
I = current = net charge drifting past a point / time interval.
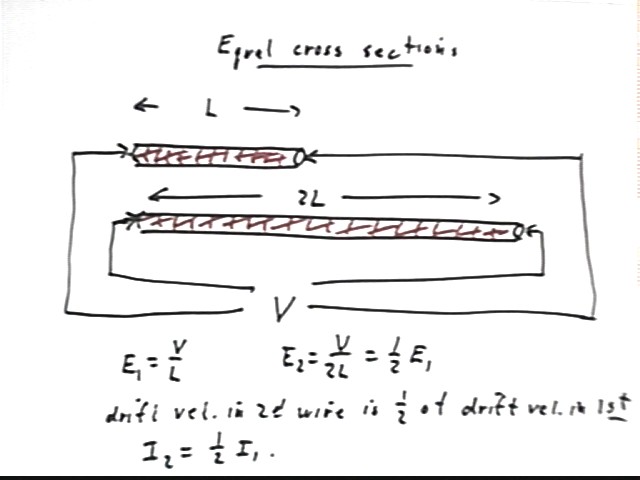
If
two uniform wires have identical cross-section, are made of the same material
but one is twice as long as the other. If
both are subjected to the same voltage then how will the electric fields in the
wires compare?
The
field is E = V / `ds. If V is the same for both, then E1 = V / L is twice as great
as E2 = V / (2 L).
The
average drift velocity of charge carriers is proportional to the electric field.
So which wire carries more current?
The
field in the first wire is double that in the second, so the average drift
velocity is higher in the first.
Since
both wires, being of identical material and equal cross-section, have the same
number of charge carriers per unit length, the greater drift velocity will bring
more charge carriers past a given point than for the second wire and the current
will be greater.
Why does it make sense to define resistance to flow of current as V / I, where V is potential difference or voltage and I is current?
High resistance means less current flow for a given voltage. Less current flow means that the denominator of V / I will be less, resulting in a larger quotient. The lower the current I, the higher will be V / I, for a given voltage.
How
does the resistance of the second wire (the one twice as long) compare to that of the first?
How therefore does length affect electrical resistance, defined as the
ratio V / I ?
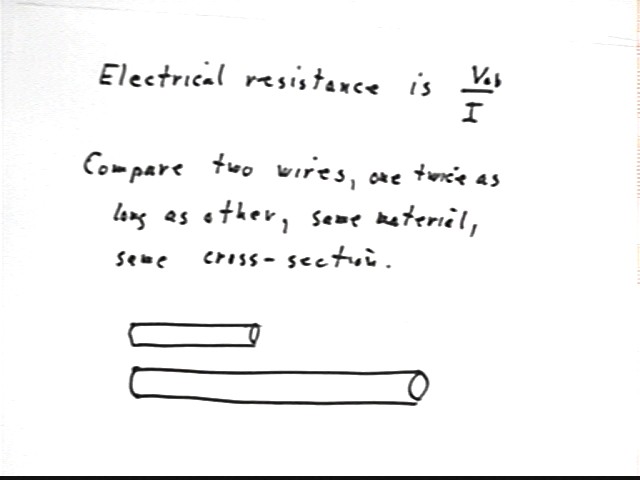
The
shorter wire had the greater electric field, therefore the greater current.
So the second wire had the greater length, lesser current and therefore
greater resistance.
If
both wires are of the same length but the second has double the cross-sectional
area of the first, then how will the currents compare? Since
lengths are the same, the electric fields will be the same and therefore the
drift average velocities will be the same. Since
the second wire has double the cross-sectional area it has twice as many charge
carriers available per unit length. It
follows that, drift velocities being identical, the second wire will carry twice
the charge of the first. How
does the resistance of the second wire compare to that of the first?
How therefore does cross-sectional area affect resistance? The
second wire carries more current for the given voltage so it has the lesser
resistance. All
other things being equal, more c.s. area implies less resistance. For
a given material what proportionality relates resistance to cross-sectional area
and length? Resistance
appears to be proportional to length and inversely proportional to c.s. area. This
is written as R
= constant * L / A, where ‘constant’ is a proportionality constant. We
generally call the proportionality constant ‘resistivity’ and denote it by
the Greek letter rho. Our equation is therefore ·
R = rho * L / A. rho
is a property of the material, and in general changes with temperature. If
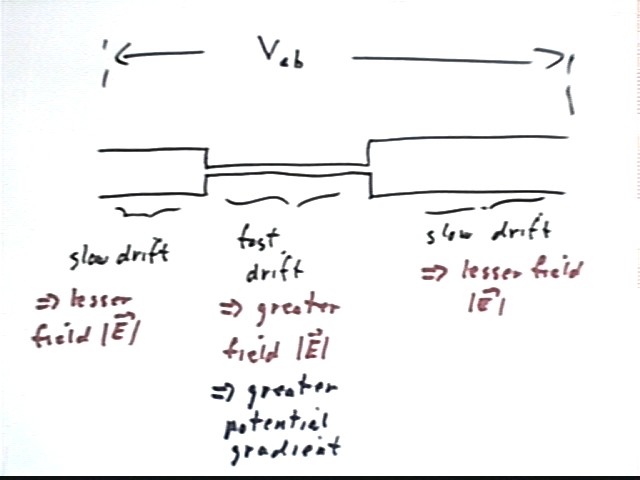
a wire runs for a ways, narrows seriously for a ways, then widens back to its
original c.s. area for a ways, what will happen to the electron flow if a
constant voltage is applied over the whole thing. The
charge carriers are pretty much like an incompressible fluid.
The flow is much faster in the narrower wire. What
does this tell you about the electric field and about the voltages across the
three segments of wire? Drift
velocity is proportional to electric field, so the field in the smaller wire is
greater. Potential
difference, or voltage, is the product of electric field and length.
So if the segments are of fairly equal lengths, the voltage across the
narrow wire will be much greater than the voltage across the wide wire.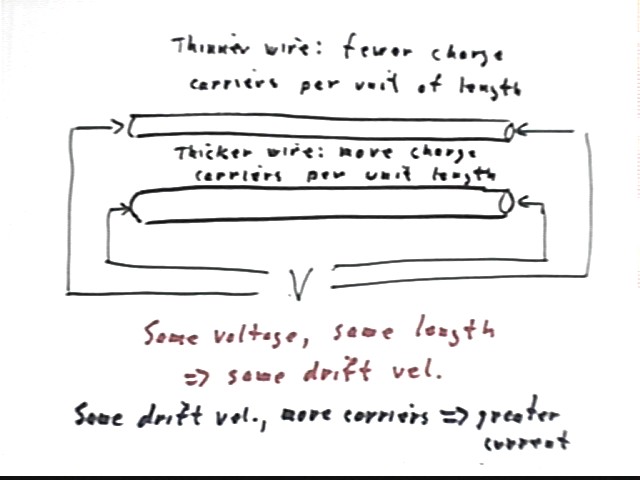
In
a circuit consisting of a source, a wire lead and a flashlight bulb (in which
the current passes through a very thin filament), where do you think most of the
voltage drop occurs?
The
wire lead is much, much thicker than the filament.
The speed of the charge carriers is therefore much, much greater in the
filament. Most of the voltage drop
therefore occurs in the filament.
Wires
that Narrow (-> series circuits)
Wires
that Branch (-> parallel circuits)
Potential
Energy Change around a Loop (Kirchoff's #? law)
Parallel-Plate
Capacitors
Discharge
of a Parallel-Plate Capacitor
Cylindrical
Capacitors