





Electric field is force / unit of charge, measured in N / C.
Potential difference is change in PE / unit of charge or work / unit charge, measure in J / C or volts.
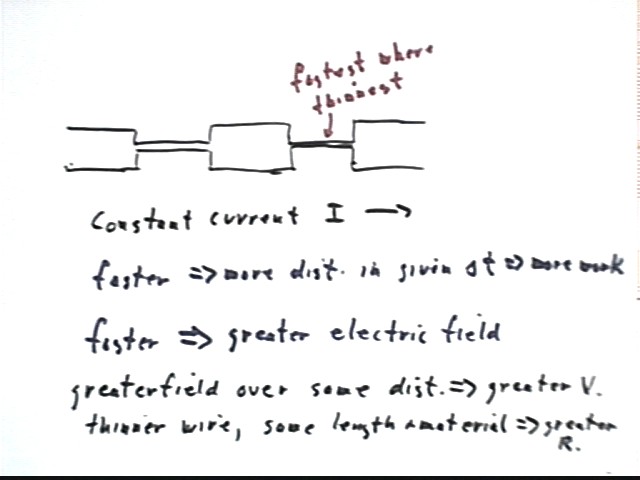
If a constant current flows through equal lengths of a thick wire, then thin wire then another thick wire, then an even thinner wire (all segments of the same length), then
through which segment(s) is the current fastest and through which is is slowest
Current is fastest through the thinnest wire (very much like the continuity equation)
through which segment(s) must we do the most, and through which the least work in a given time period
In the thinnest wire we're moving fastest, also perhaps against greater force, so do work at the greater rate.
which segment(s) have the greatest and which the least resistance
As seen in the preceding class, resistance of a given material is proportional to c.s. area and inversely proportional to length.
over which segment(s) is the voltage greatest and over which the least
over which segment(s) is energy dissipated at the greatest and over which at the least rate
if a constant voltage is maintained from the leftmost to the rightmost point then where is the voltage changing the most quickly and where the least quickly?
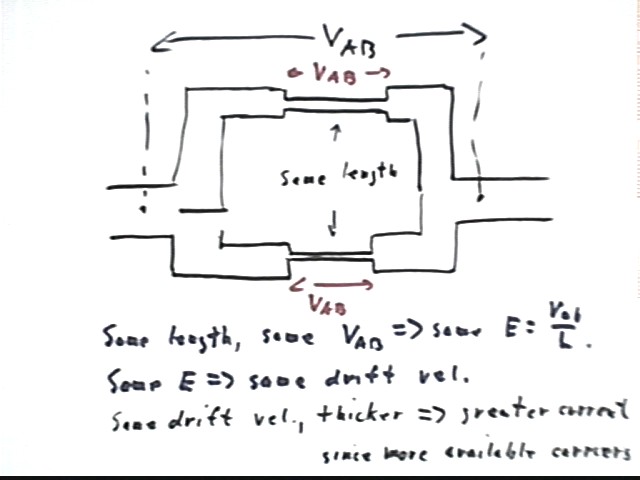
If a constant voltage is maintained between points A and B, and if two wires of equal length but with one thinner than the other connect points A and B, then
through which wire is the drift of the current faster and through which it is slower?
The lengths of the wires are equal and potential changes are equal, the electric fields are equal. The equal electric fields imply equal drift velocity.
which wire carries the greater current
The thicker wire has more charge carriers available per unit length so with electrical fields being equal the thicker wire carries more charge.
through which wire must we do the most, and through which the least work in a given time period
The thicker wire carries more charge per unit of time. Potential difference is work per unit of charge. So more work is done per unit of time in the thicker wire. (Same number of J / C and more C / second implies more work / second).
which wire have the greater and which the lesser resistance
Resistance is proportional to length and inversely proportional to c.s. area so the resistance in the thinner wire is greater. We see this also because, as noted above, the thinner wire in this case carries less current over the same potential difference.
over which wire is the voltage greater
The voltages are the same.
over which wire is energy dissipated at the greater rate
The thicker wire carries more current over the same potential difference so dissipates energy at a greater rate.
if a constant voltage is maintained from the leftmost to the rightmost point then where is the voltage changing the most quickly and where the least quickly?
The distances are the same so voltage changes at the same rate as we move across either wire.
For a current of 3 amps over a resistance of 5 ohms what must be the voltage?
We know that I = V / R. We want to find V so we solve for V, obtaining V = I * R = 3 amps * 5 ohms = 15 volts.
If current I passes thru resistance R then what is the voltage?
Since I = V / R we have V = I * R .
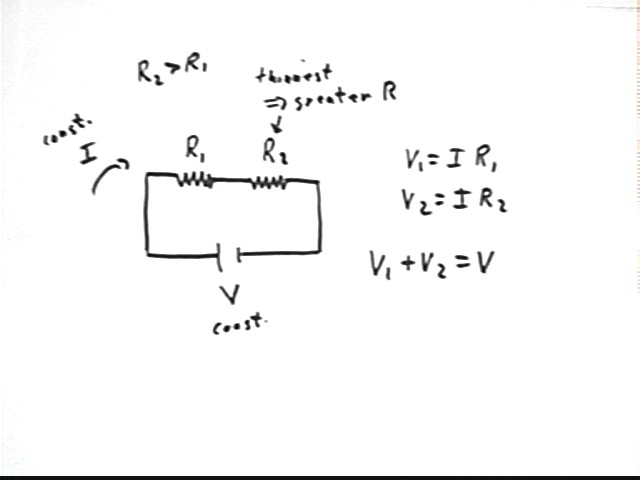
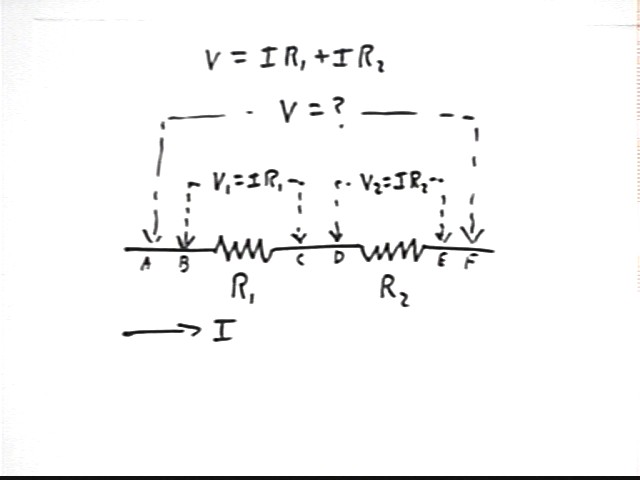
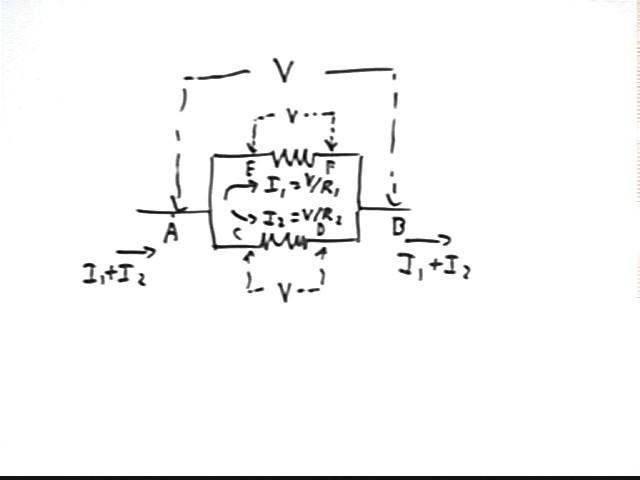
For two resistors in series, with resistances R1 and R2 and a constant voltage V across the combination, give an expression for V in terms of current I and resistances R1 and R2?
As depicted in the figure there is no voltage change from A to B, from C to D or from E to F, due to the negligible resistance in connecting wires.
So as we move from A to F the only voltage changes are V1 = I R1 and V2 = I R2; the net change in voltage is V = V1 + V2 = I R1 + I R2.
If R = V / I then what is the resistance of the combination of the preceding question?
The current is I and the voltage is I R1 + I R2. So
R = V / I = (I R1 + I R2 ) / I = R1 + R2.
For two resistors in parallel, with resistances R1 and R2 and a constant voltage V across the parallel combination, what are the currents I1 and I2 in the two resistors?
The potential difference V is the same across R1 is the same as the potential difference across R2. So currents are I1 = V / R1 and I2 = V / R2.
If R = V / I, where I is the total current, then what is the resistance of the combination of the preceding question?
The total current is I1 + I2 = V / R1 + V / R2.
Since R = V / I we have
R = V / (V / R1 + V / R2) = 1 / (1/R1 + 1/R2).
This is usually written in the form
1/R = 1/R1 + 1/R2.
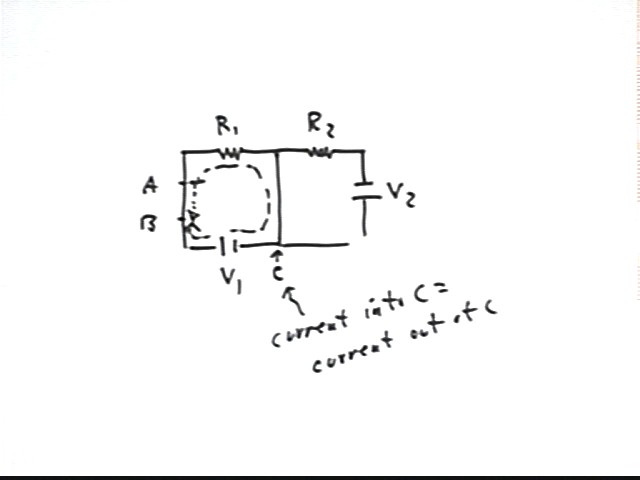
Suppose that a circuit is comprised of two loops, as indicated in the figure.
What is the net change in electric potential between the points A and B, which are on the same wire lead?
There is no resistance between A and B so even if current is flowing, as is likely, there is no potential difference.
How much charge do you think accumulates in an hour at the branching point C? How much in a millisecond?
Wires that Narrow (->
series circuits)
Wires that Branch (->
parallel circuits)
Potential Energy Change
around a Loop (Kirchoff's #? law)
Parallel-Plate Capacitors
Discharge of a Parallel-Plate
Capacitor
Cylindrical Capacitors