We know light has a wave nature (diffraction, refraction, etc.).
Quick introduction to the particle nature of light:
Light propagates in a vacuum with velocity 3 * 10^8 m/s.
If the wave motion associated with a light beam has frequency f then by measuring the potential energies of electrons emitted from a photoelectric metal we find that the wave is in some sense comprised of mysterious particles called photons each having energy
E = h f
where h = 6.63 * 10^-34 J s.
Light of wavelength 500 nanometers ejects electrons from a photoelectric metal.
What is the greatest energy any one of these electrons can have, assuming that no electron is lucky enough to absorb the energy of more than one light photon?
E = h f; we know h and wavelength. We also know propagation velocity c = 3 * 10^8 m/s.
From the relationship between frequency, wavelength and propagation velocity we find that
f = 3 * 10^8 m/s / (500 nm) = 3 * 10^8 m/s / (5.00 * 10^-7 m) = .6 * 10^15 cycles/sec = 6 * 10^14 Hz.
Now using E = h f we get
E = 6.63 * 10^-34 J s * (6 * 10^14 s^-1) = 4 * 10^-19 J.
How many volts of opposing potential difference could an electron with this energy overcome?
A charge q moving through potential difference V overcomes potential difference q V. This is because V is the work per unit of charge required to move a charge from one point to another.
An electron with 4 * 10^-19 J can overcome an opposing potential difference of
q V = 4 * 10^-19 J.
The charge of an electron is -1.6 * 10^-19 C. So we can overcome potential difference V such that
-1.6 * 10^-19 C * V = 4 * 10^-19 J or
V = 4 * 10^-19 J / (-1.6 * 10^-19 C) = -2.5 J / C or -2.5 V.
How many Joules are necessary to give an electron enough KE to overcome an opposing potential difference of 1 volt?
We just saw that 4 * 10^-19 J gets us through a 2.5 volt opposing potential difference. We only need enough to get us thru 1 volt so the answer will be less that 4 * 10^-19 J.
We need energy equal to
q * V = 1.6 * 10^-19 J * 1 volt = 1.6 * 10^-19 Joules.
We call this energy an electron volt.
On the Earth's surface, if the Sun is 'directly overhead' (which happens only in the tropic), the energy flux from the sun is about 1000 watts / square meter. Most of this energy comes in the form of electromagnetic radiation, and most is in the visible spectrum. The average wavelength of this radiation is around 600 nm.
About how many photons therefore fall on a square meter in 1 second?
Each photon carries energy E = h f, using the frequency of 600 nm radiation as an average. We know how much energy falls in a second so we easily find the number of photons falling in a second.
A beam of electrons acts like a wave (even if the electrons pass through a diffraction grating one at a time). The wavelength of the beam is
lambda = h / p,
where p is the momentum of a single electron.
What is the wavelength of a beam of electrons in which each electron has kinetic energy 5000 electron volts? (Note that the mass of an electron is about 9 * 10^-31 kg).
The mass is found from .5 m v^2 = KE, so that
v = sqrt(2 * KE / m)
The momentum is
p = m v = m * sqrt(2 KE / m) = sqrt(2 KE m)
Evaluating we find that p = sqrt( 2 * (5000 * 1.6 * 10^-19 J) * 9 * 10^-31 kg) = 3.8 * 10^-23 kg m / s.
So the wavelength is
lambda = h / p = 6.63 * 10^-34 J s / (3.8 * 10^-23 kg m/s) = 1.8 * 10^-11 m.
from before:
from 4/18
If we charge the 1 Farad capacitor to 8 V and discharge it, without intervening resistance, thru the aluminum strip, how long does it take the capacitor to fall to 4 volts?
An eyeball estimate tells us that is takes much less than a second--probably between 1/10 and 1/4 second.
How much charge do you think flows during this time?
The 1 Farad capacitor holds 1 Coulomb per volt. If 4 volts are lost then 4 Coulombs are lost.
What maximum current do you think occurs in the aluminum strip?
4 Coulombs are transfered thru the circuit from one plate of the capacitor to the other during a time span somewhere between 1/10 sec and 1/4 sec. The average current is therefore somwhere between (4 C) / (1/10 sec) = 40 amps and (4 C) / (1/4 sec) = 16 amps.
Just as the voltage drops from 8 V to 4 V in a nonlinear fashion the maximum current will drop from some max to a min value which is half the max. The average current will be somewhere in between; since the drop is exponential as opposed to linear the average will be closer to the min than the max.
If the average current is 16 amps we might estimate that the max current might be about 25 amps. Analysis of an exponential function could give us a better estimate, but remember that we're already pretty deep into inaccurate measurements. Similarly an average current of 40 amps would correspond to a max current of perhaps 60 amps.
Since the r vector from the midpoint of the segment is perpendicular to the current, since the length of the segment is much less than r, the magnetic field is B = k ' * ( I L ) / r^2 * sin(theta) = 10^-7 T m / amp * ( .02 amp m) / (.10 m)^2 * sin(90 deg) = 2 * 10^-5 T.
If we regard the 26-cm aluminum strip as a series of 2-cm segments, with the previous segment being in the middle, then what is the field at the previous field point due to the next segment to the right?
If we take the center if the first segment as the origin of an x axis running along the strip, then the next segment to the right is a .02 m segment centered 3 cm to the right of the center of the first segment (if you start at the origin, i.e., the center of the first segment, and move 1 cm to the right you are at the end of that segment). The segment of this question runs from x = 1 cm to x = 3 cm, and is centered 2 cm from the origin.
The r vector from the center of the segment to the field point is therefore the hypotenuse of a right triangle with sides .02 m and .10 m. Thus r^2 = (.02 m)^2 + (.10 m)^2 = .0104 m^2.
The sine of the angle between the r vector and the current is sin(theta) = .10 m / sqrt(.0104 m^2) = .98.
*&*& B = k ' * L / r^2 * sin(theta) and denominator in sin(theta) calculation is sqrt(.0104 m^2), not sqrt(.104 m^2).
What is the field due to a 2 cm segment at distance x from the origin?
The r vector from the center of the segment to the field point is the hypotenuse of a right triangle with sides x and .10 m. Thus r^2 = x^2 + (.10 m)^2 = x^2 + .01 m^2. In the figure below the units are suppressed and we understand all distances to be in meters.
The sine of the angle between the r vector and the current is sin(theta) = .10 m / sqrt(.01 m^2 + x^2).
Thus B = k ' * L / r^2 * sin(theta) = 2 * 10^-6 T m^2 / (.01 + x^2)^(3/2), as shown below.
*&*& the .02 amp m used below is in error; should be 2 amp m and the numerator in the result should be 2 * 10^-8 T m^3 ...
Is the field in the preceding calculation in the same direction as the field obtained in the first calculation?
The direction of the current is along the x axis in both cases. In both cases the plane formed by the x direction and the r vector is the same (this follows from the fact that the present r vector lies in the plane formed by the x axis and the first r vector). If we point the fingers of the extended right hand in the direction of the positive x axis and orient the hand so that when the fingers are curled toward the palm they will 'turn' the x axis toward the r vector the thumb will in every case point downward, perpendicular to the plane formed by these vectors.
So the magnetic fields are in the same direction in every case.
We have just shown that the field due to a 2 cm segment centered at position x is approximately B(x) = 2 * 10^-8 T m^3 / (.01 m^2 + x^2)^(3/2), and that the fields of all the segments are in the same direction. What therefore would be our approximation to the total field of our 26 cm wire, assuming the first segment to be centered at the halfway point of the wire? Note that the wire would therefore run from x = -13 cm to x = 13 cm.
Our 26-cm wire consists of the center segment, which spans out to a distance of 1 cm from the center, plus the segments centered at x = 2 cm and x = -2 cm, with pairs of segments centered also at distances of 4, 6, 8, 10 and 12 cm from the center. Recalling that B is defined in terms of x in meters, we see that the fields of these segments are B(0), B(.02), B(.0-2), B(.04), B(.0-4), ..., B(.12), B(-.12).
Since the only reference to x in the equation for B(x) is the x^2 term in the denominator, B(.02) = B(.0-2), B(.04) = B(.0-4), ..., B(.12) = B(-.12).
So the total field is B = B(0) + 2 B(.02) + 2 B(.04) + ... + 2 B(.12). Using a computer algebra system to calculate this sum we obtain B = .0001586 T.
This is only an approximation, since we are using the center point of each segment to stand for the distance of each point on that segment from the field point. This works to the extent that our segments are short compared with their distances from the field point. Since the length of the segment is only about 1/5 of the distance to the field point the approximation used here is pretty accurate. It turns out that using the methods of calculus (shown below for University Physics students) to obtain the exact field we obtain B = .0001582 T, very close to the .0001586 T obtained above.
If we have a current segment of length `dL at positoin x then what is the corresponding field contribution at a point lying a units from the center point along a line perpendicular to the x axis, assuming a current I in the x direction?
The product I `dL is the source of this field contribution, and by the Pythagorean Theorem the r vector has length r = sqrt(a^2 + x^2). The sine of the angle between the r vector and the x axis is thus a / sqrt(x^2 + a^2).
The field contribution is thus B = k ' I `dL / (sqrt(a^2 + x^2))^2 * 1 / sqrt(a^2 + x^2) = k ' I `dL a / (a^2 + x^2)^(3/2).
University Physics students only: Consider a typical segment of length `dx lying near position x along the x axis. Find the field of the typical segment, form a Riemann Sum of a partition of such segments and obtain the integral which represents the field at distance a from a strip of current, lying along a line through the center of the strip at distance a.
The figure below depicts a segment of length `dx lying at position x along the x axis. We see that I `dL = I `dx and as before r^2 = x^2 + x^2 and sin(theta) = a / sqrt(a^2 + x^2). This gives us current contribution
If the strip is partitioned into segments of length `dx then the total current is the sum of all such contributions, with the sum running from one end of the strip to the other. This sum is depicted below.
We can factor the constant k ' I a out of the sume. As `dx -> 0 the remaining sum approaches the integral depicted below. The limits on the integral are dictated by the positions of the ends of the segment.
If the wire is very long the segment runs from -infinity to infinity, and it can be shown using the methods of calculus that the resulting field is 2 k ' I / a. If I = 100 amps and a = .10 m, corresponding to the example used earlier, this gives us B = .00020 amps. Note that our approximation for a strip only 26 cm long gave us B = .00016 amps, approx.. From this we see that even if the strip was extended to infinity most of the field would be due to the portion of the infinite strip within 13 cm of the center point.
If we integrate the same function from x = -.13 to x = .13 we obtain the accurate field of our 26-cm strip. The result is the B = .0001582 T quoted earlier.
Some of the computer algebra expressions and results quoted above are depicted below. University Physics students should know the techniques used to evaluate the integrals quoted here (start by substituting x = tan(theta); this is one of the standard integrals performed by trigonometric substitution in most first-year calculus classes).
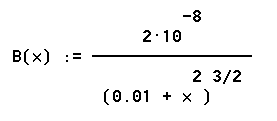
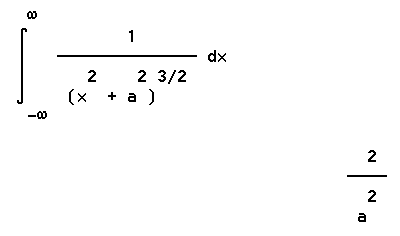
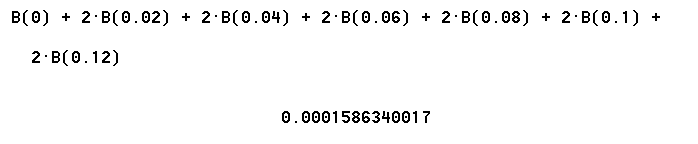
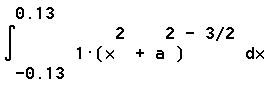 gives us 1.582 *
10^-4
gives us 1.582 *
10^-4