Bernoulli Equation Comparing two points, includes continuity equation

Bernoulli's Equation

We apply Bernoulli's Equation to a number of situations, most related to the system analyzed in the experiment.

Bernoulli's equation relates the values of v, h, rho, g and P at different points.  For some situations all these quantities could be considered variable (e.g., in the atmosphere, where density is certainly variable and even the acceleration of gravity changes slightly with altitude).

Note for situation of the experiment:

• For an (almost) incompressible fluid like water, the density rho will remain constant.  For a compressible gas, rho would be variable.
• The acceleration g of gravity does not vary appreciably over the scale of any water-filled system we are likely to observe. 

Thus only v, h and P are considered variable for this model.

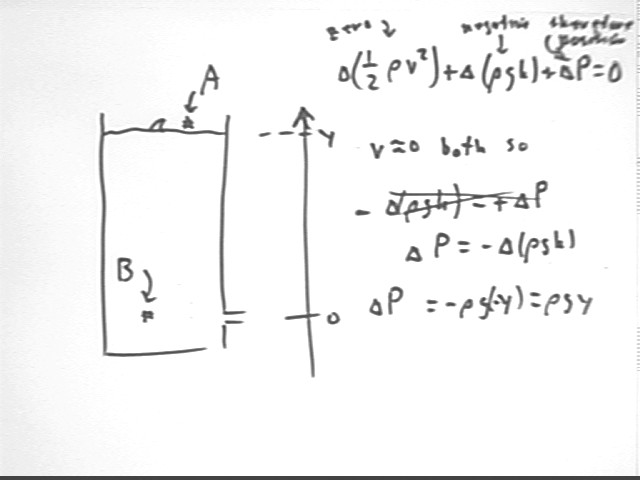
Compare v, h and P at the water surface with v, h and P at the instant the water exits the hole.

Comparing the state of the system at point A at the water surface with the state point B, where the water has just exited the container, we observe that

• the velocity v_A at point A is much less than v_B, making v_A^2 much, much less than v_B^2 so that v_A^2 is negligible and can be take to be approximately zero
• altitude from point A to point B changes by -y, where y is the depth of water relative to the hole
• both points are open to the atmosphere, and atmospheric pressure varies by a negligible amount form A to B, so pressure at both points is equal and `dP is effectively zero.

Thus the change in 1/2 rho v^2 is 1/2 rho v_B^2, the change in rho g h is rho g * (-y) and the sum of these changes is zero.

• The resulting equation tells us that v_B = sqrt(2 g y).

Note that we previously obtained the same result for v_B using PE to KE conversion.  In fact conservation of energy is one of the principles used to derive Bernoulli's Equation.

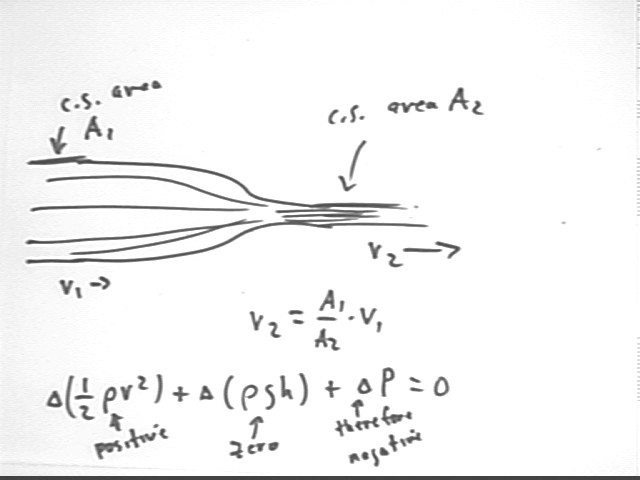
Compare v, A and P for a fluid running through a pipe at two points, one just before and one just after the pipe narrows.

Consider a fluid in a closed system such as the one pictured below, where a pipe is filled with water then closed.  An impeller at the bottom circulates fluid around the pipe, which narrows at the indicated point.  Bernoulli's Equation will tell us that the pressure in the narrow section of pipe will be less than that in the wide section.  The continuity principle tells us that water is moving faster in the narrow part of the pipe. 

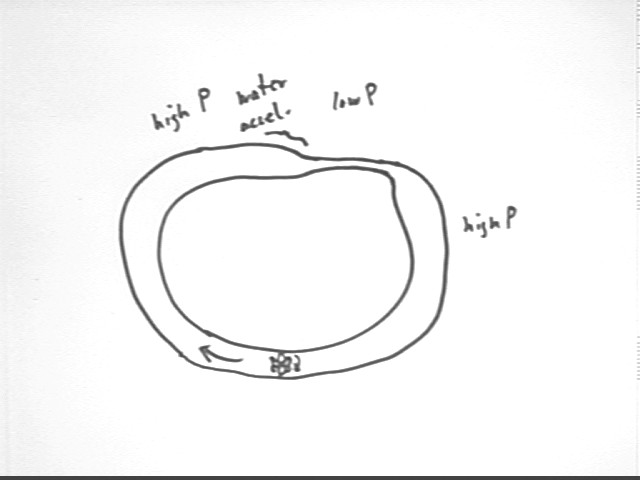
Where the pipe narrows there is negligible change in altitude h so that `d(rho g h) = 0.

v2 = A1 / A2 * v1 so that the velocity v2 in the narrow part of the pipe is greater than the velocity v1 in the wider part, so moving from point 1 to point 2 results in an increase in 1/2 rho v^2.

Bernoulli's Equation therefore tells us that since 1/2 rho v^2 increases and rho g h remains the same, the change `dP in pressure is negative.

Your textbook goes into all the details but the key is that to speed up the water we need greater pressure behind than in front, so that pressure in the wider part must be greater than that in the narrow part.

• More accurately we can say the analysis is based on the work done to accelerate the water, which is directly related to the pressure difference.

Comparing point A inside the container, at the level of the outflow, with point B directly outside we observe that

• pressure from A to B decreases so `dP is negative
• altitude h remains constant so `d(rho g h) is zero

It follows that 1/2 rho v^2 must increase, so that v increases.

Noting that v_A is negligible we proceed to find the expression for v_B.

Recommendation:  review the previous analysis, based on the work done on the 'plug' of water in the tube, of the exit velocity of the water.

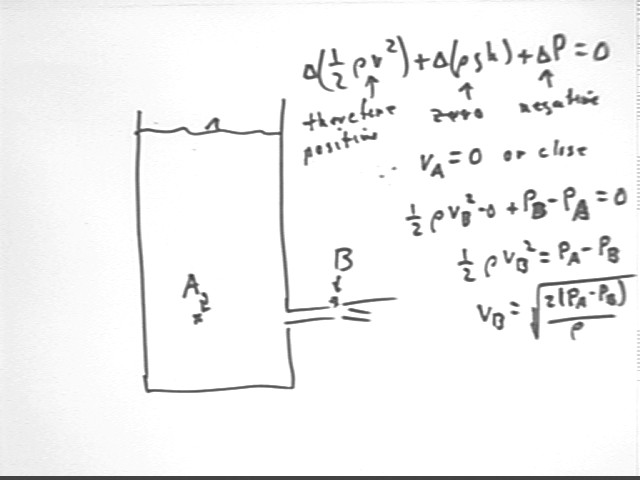
Compare point A at the water surface to point B at the level of the hole, but inside the container.

We can also compare point A at the water surface to point B at the level of the hole, but inside the container.

• velocities at A and B are low so that 1/2 rho v^2 is effectively zero at both points
• altitude h decreases from A to B so that `d(rho g h) is negative

it follows from Bernoulli's Equation that the change `dP in pressure is positive.

Since the change in h is -y we find that the pressure change is

• `dP = - `d(rho g h) = -(rho g * (-y) ) = rho g y.

The pressure at depth y is greater than the pressure at the surface by rho g y, consistent with the rho g h we obtained previously by considering the weight of a water column of given height and cross-sectional area.