Fluid Element from Hole at Depth y

We now consider a container filled to depth y, relative to a hole from which fluid can exit.

The demonstration is class showed such a system, and showed that as water exited the hole and decreased the depth of the water the velocity of the exiting water decreased, decreasing the rate at which the depth decreases.

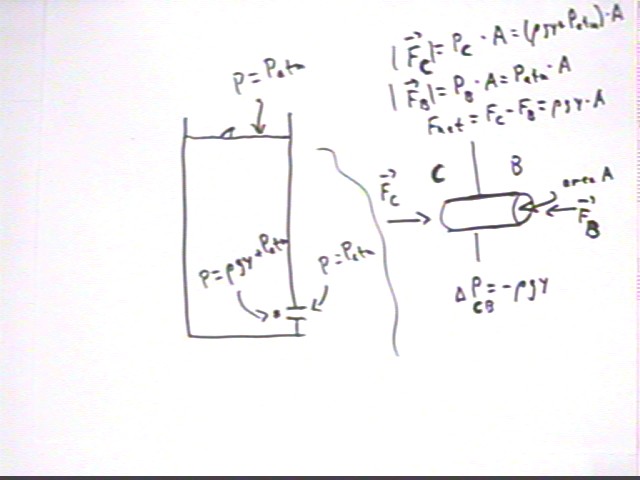
The pressure of the water is the source of the force which accelerates water out through the hole.

• The pressure at the upper surface of the water is atmospheric pressure, represented Patm.
• The fluid adds pressure rho g y at the level of the hole, so that inside the container, where the water is stationary, the pressure is rho g y + Patm.
• The pressure outside the hole is Patm.

If we consider the water to flow thru a short tube on its way out of the container, and if we assume that the only forces exerted are by the pressure (the model will simplify the situation and ignores frictional forces, e.g. between water and tube walls, and also by assuming the water just inside the container next to the tube to be stationary) then we see that the water in the tube experiences force Fc = (rho g y + Patm) * A to the right and force Fb = Patm * A to the left.  

• The net force on the water in the tube is therefore Fc - Fb = rho g y * A.

Considering the water in the tube, we know the net force on the water.  If we know the mass of the water we can therefore find its acceleration.

• Assuming tube length L we find that the volume of the tube is A * L, so that the mass of the fluid in the tube is mass = rho * A * L.
• We conclude that the water in the tube experiences acceleration a = Fnet / m = rho g y * A / (rho * A * L) = g y / L.
• Note that this acceleration is independent of the density of the fluid.  The denser the fluid the greater the fluid pressure, but also the greater the mass of the fluid in the tube.  The two effects 'cancel' and we find that acceleration depends only on gravitational acceleration, depth and tube length.

We now have enough information to find the velocity of the exiting water.  We know that before entering the tube the velocity of the water was presumably zero, that its acceleration is g y / L and that the accelerating force acts through displacement `ds = L.

• Using the fourth equation of motion vf^2 = v0^2 + 2 a `ds, with vf = vExit, we conclude that vExit = sqrt ( v0^2 + 2 a `ds ) = sqrt ( 0 + 2 * (g y / L) * L ) = sqrt( 2 g y).

We also observed that when the system is in free fall (having been dropped or tossed upward) there is no flow from the opening.  This is because the pressure in the fluid results from the normal force needed to hold the fluid stationary against gravitational forces; if the system is in free fall its acceleration is equal to that of gravity, so that the net force on the fluid is equal to its weight, and zero normal force is required.  This results in zero pressure.  Hence there is no force to accelerate the fluid out of the hole, and the flow ceases.