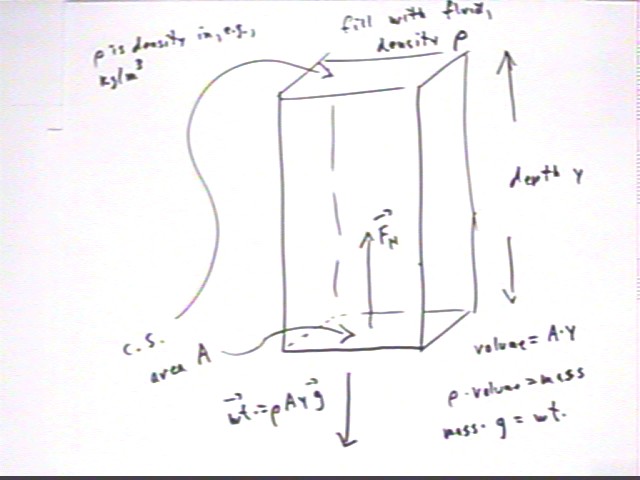
Pressure at depth y using container of uniform cross-section

The situation depicted below will demonstrate how the pressure in a stationary fluid depends only on the density of the fluid, the depth and the gravitational acceleration.

• We consider a container with uniform cross-sectional area A, filled to depth y with a fluid of density rho.  
• The volume of the fluid is A * y, so that its mass is density * volume = rho * A * y and the weight of the fluid is therefore weight = - rho A y g (implicitly using the upward direction as positive).
• Since the fluid is stationary its acceleration is zero, so the net force on the fluid is zero.  There must therefore be (an)other force(s), equal and opposite to the weight.
• This force is the normal force exerted by the base of the container on the fluid.

The force Fnormal is therefore 

• Fnormal = rho g A y.

This force is equally distributed over the base of the container, so it makes sense to speak of the force per unit area.

This force per unit area is the pressure.  A simple calculation shows us that at depth y the pressure is

• P = Fnormal / A = rho g A y / A = rho g y.