Experiments 1-4
Note: It is suggested the Experiments 1, 2
and 3 be done in the same session.
Experiment 1: Measuring
Temperature with an Uncalibrated Thermometer
Using an uncalibrated thermometer and a ruler we measure the
temperatures of freezing and boiling water and room temperature. Using the linearity
of the Celsius scale and appropriate assumptions about thermometer we infer the Celsius
temperature of the room.
In this experiment you will use an uncalibrated
thermometer (one with no marks on it) and a ruler to obtain
reasonably accurated indications of temperatures according to different
temperature scales.
Given an uncalibrated
thermometer and a plastic ruler, obtain a sample of ice
water and a sample of boiling water and demonstrate that the
temperature of the ice water is less than that of the boiling water, and
that the temperature of your room lies between that of ice water and of
boiling water.
- The ice water should have approximately equal
parts ice and water, and should be stirred constantly during the
measurement of temperature.
- The boiling water should be actively boiling,
or should have been actively boiling within a couple of seconds before the temperature is
observed.
- The plastic ruler should not be
permitted to contact the boiling water.
- You should give quantitative data to
support your contention that the temperature of the boiling water is greater than that of
the ice water.
- Explain why you think that your conclusions
follow from your observations. This explanation should not be
based on the assumption that thermometers go up when temperature goes up.
You should explain what is going on in the thermometer and how this is
related to what we call temperature.
If you assume that the temperature
of the ice water was 0 Celsius while that of the boiling water
was 99 Celsius (as is the approximately the case at the elevation of VHCC), then
what do your data indicate is the Celsius temperature of the room?
- How did you use your data to get your result?
- What assumptions did you make to
get your result?
If you assume that the temperature of the ice water
was 32 Fahrenheit while that of the boiling water was 210
Fahrenheit (as is the approximately the case at the elevation of VHCC), then what
do your data indicate is the Fahrenheit temperature of the room?
- How did you use your data to get your result?
- What assumptions did you make to get your result?
Experiment 2: Thermal Content
of Water, Steel, Rock
Using the uncalibrated thermometer
and ruler we measure the temperature of a known quantity of water before a sample
previously immersed in boiling water is introduced into the system. We then measure
the temperature of the water after the new system has come to equilibrium. From the
masses of the water and the sample we estimate the thermal energy content, per Celsius
degree per gram of the substance, as a fraction of that of water.
In this experiment you will determine how much thermal
energy is required to raise the temperature of 1 gram of
steel, then of stone, by 1 degree Celsius, given the amount of thermal
energy required to raise the temperature of 1 gram of water by 1 degree Celsius.
Place the large steel washer in boiling
water and leave it there for at least 5 minutes. Do not let
the washer come in contact with the bottom or sides of the
container in which you are boiling the water--the washer should be in contact
with just the water. (Suggestion: Suspend the washer
by a thread).
In a Styrofoam cup place approximately
a 1 cm depth of water at room temperature ,
being sure that there is enough water to cover the washer and the bulb
of the thermometer and to permit stirring of the water.
- When the washer has been in boiling water for least
5 minutes, obtain the data needed to determine the temperature of the water in
the Styrofoam cup, then quickly transfer the washer
to the Styrofoam cup and begin stirring the
water.
- Determine when the temperature of
the water reaches its maximum, and take data to
determine this maximum temperature.
- Finally determine the mass of the water
in the cup and the mass of the washer.
- To determine the weight of the ater, use the
graduated cylinder (the rain gauge), using the information that 24 milliliters of water
will raise the water level in the gauge by 7.9 cm, and that 1 milliter of water has a mass
of 1 gram.
- If you have no other means of measuring the mass of
the washer, you can assume a mass of 35 grams.
Now analyze the energy transfers between
water and washer:
- You certainly observed that the temperature of
the water increased.
- Given that every gram of water required
approximately 4.19 Joules of thermal energy for every
Celsius degree of temperature increase, how many Joules of thermal energy
did the water obtain from the washer, assuming
at first that the water did not gain or lose any energy from its surroundings?
- What was the temperature change of
the washer, assuming that its temperature was 99 Celsius when it was
immersed in the water?
- How much thermal energy was lost by
each gram of the washer?
- How much thermal energy was lost, per
Celsius degree of temperature change, by each gram of the
washer?
- How accurate you think the assumptions
made in this analysis actually are, and how much difference do
you think the uncertainties and/or errors would have on the final result?
Repeat this experiment for a small
rock whose mass is approximately that of the washer.
- What can you say about the relative capacity
of steel and stone for retaining
thermal energy?
Experiment 3: Heat of Fusion of
Water
By measuring temperatures before and after
introducing a known amount of ice at its melting point in a known amount of water we
determine the thermal energy per gram required to melt ice at its melting point.
In this part of experiment 3 you will determine how
much thermal energy must be added, per gram of ice at 0
C, to melt the ice into water at the same temperature.
In a Styrofoam cup place approximately 200
ml of hot water.
Obtain approximately 1 cup of fine powdered
snow, if possible, or 1/4 cup of finely chopped ice.
If you use ice, dry it as much as possible with
paper towels before placing it in the hot water.
- Determine the temperature of the ice
or snow. If the temperature is not steady at 0 Celsius, keep
measuring until it is.
- Determine the temperature of the hot
water, then immediately disperse the powdered snow in
the water, 1 heaping tablespoon at a time, or dump the chopped ice
into the water.
- Keep stirring vigorously until all
the ice or snow is melted (snow should melt almost instantly, which is why it is
preferable).
- As soon as all the ice or snow is melted,
determine the temperature of the water.
- Find the mass of the water now
in the cup (measure it using the graduated cylinder).
Analyze your results to determine how many Joules
of thermal energy were transferred from each gram of the ice or
snow to the water that was originally in the cup, before and after melting.
- From the mass of the water originally in the
cup and from the fact that 4.19 J of thermal energy are lost by each gram of this
water for every degree its temperature decreases, determine the amount of thermal
energy lost by this water.
- From the mass of the ice or snow added
to the system, determine the amount of thermal energy gained by this mass
as its temperature increased from 0 Celsius, just after
it melted, to the final temperature of the system.
- From the previous two results determine the amount
of thermal energy lost by the ice or snow before
it melted, and determine the amount of thermal energy lost per gram of
ice or snow during the melting process.
- Sketch a graph of the temperature of
a 1 sample gram of ice or snow, considered to be originally at 0 Celsius, vs.
thermal energy added to the sample.
The
actual situation is somewhat complicated, since the melted
part of the ice changes temperature while the unmelted
part stays at constant temperature 0 Celsius. An accurate
graph would have to somehow depict the infinite variety of
expected average temperatures of different parts of the ice as they melt
at different times, which is much too complicated.
We can simplify the situation and make it possible to
graph if we can think the material that make up the ice as
an isolated unit within the water, all at the same temperature at
any instant. It would stay at 0 Celsius until it melts,
then climb in temperature as a unit as it exchanges
thermal energy with the water.
Experiment 3.5: Specific Heat
by Deflection of Temperature Relaxation Curve
By first observing the time
dependence of the temperature of a sample of ice water in a constant-temperature room,
then by observing the discontinuous 'jog' in the curve which results from the introduction
of a sample of known mass and temperature, we infer the specific heat of the sample.
(required for Physics 201 and 241
only; optional for Physics 121)
In this experiment we will observe Newton's
Law of Cooling.
We will then use our understanding of temperature
relaxation curves to devise a way to compensate, when measuring
specific heats, for the unavoidable thermal energy transfers between the system
being observed and its environment.
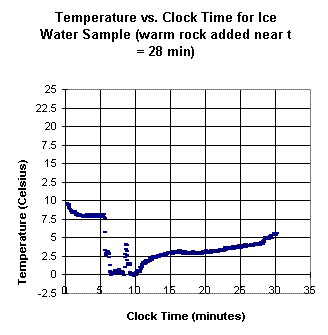
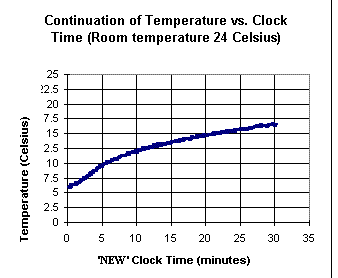
The first two graphs shown above
depict temperature vs. clock time for an ice water sample into
which a warm rock is added near clock time t = 28 minutes, after the ice
has melted. The second graph is a continuation of the first,
after approximately a 1-minute lapse. The 'new' clock time starts at the
end of this 1-minute lapse. Note the 'gap' in the temperature corresponding to the
1-minute delay.
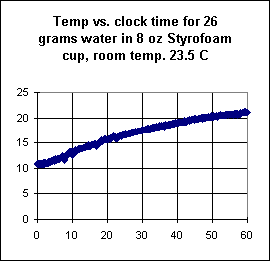
The third graph depicts temperature
vs. clock time for the same amount of water without the addition
of the rock.
- Though it is not labeled, it should be clear by
comparison with previous graphs that temperature is in Celsius and clock time in in
minutes.
From the graphs, estimate how much thermal
energy, per gram of water, was gained from the rock.
Explain how you made your estimate.
If the mass of the water was 30
grams and that of the rock 15 grams, estimate the specific
heat of the rock, in Joules per gram per Celsius degree.
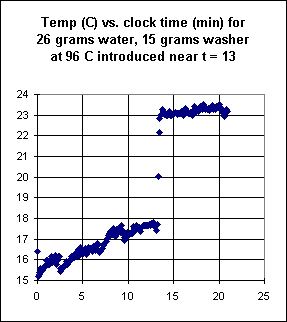
The graph shown below depicts the temperature response when a metal washer is
introduced to the water.
- How much thermal energy does it appear is gained by the water from the washer?
- Which estimate do you have more faith in, the energy gained from the washer or
the energy gained from the rock in the previous situation? Why do you answer as you
do?
Experiment 4
Using a U-shaped length of plastic tubing
sealed at one end and inserted through a stopper in a soft drink container at the other,
with a column of liquid between the sealed end and the container, we measure the volume of
the air column in the sealed end of the tube as a function of the temperature in the
container. From these measurements we estimate absolute zero.
In this experiment you will observe how the air
pressure in a sealed container of fixed volume depends on temperature.
As shown on the video clip, insert the stopper and
pressure tube into a 3-liter plastic soft drink bottle. Note that the pressure tube is sealed
at one end and has an air space at this end, with the air space blocked
by water in the U part of the tube.
Measure the length of the air
column in the tube with the entire system at room temperature.
Record room temperature.
- Completely immerse the bottle in ice
water at 0 Celsius. Give the air in the bottle about 5
minutes to come to the temperature of the ice water, and measure the length
of the air column.
- Repeat using room-temperature water.
Measure the length of the air column and water temperature.
- Repeat with the bottle in warm water,
about the temperature of a hot bath, and measure the length of the air
column and water temperature.
- Repeat with the bottle in hot water at
approximately 55 Celsius.
- Repeat for a water temperature of approximately 75
Celsius; note carefully whether the bottle becomes distorted by the temperature
of the water and if so, do not use this reading.
Analyze your results.
- Organize your data into a table of air column
length vs. water temperature. Leave a column for pressure, which
will be calculated below.
- Assuming that pressure is inversely
proportional to air column length, we have the relationship P
= k / L, where P is pressure and k is column length. Assuming in addition that
the pressure in the system when you measured it at room temperature was
equal to 1 atmosphere, determine the value of k.
- Using P = k / L with this value of k,
determine the pressure in atmospheres for each of the
measured column lengths.
- To your table addthe column containing
the pressures.
- Construct a graph of pressure
vs. Celsius temperature and fit a straight line to graph.
- From your straight line estimate the
following:
- The pressure that would result from
a temperature of 100 Celsius, provided that the bottle could remain
undistorted at this temperature.
- The pressure that would result from
temperature of 1000 Celsius, provided that the bottle remained
undistorted.
- The temperature at which the pressure
would be 1/2 of atmospheric pressure.
- The temperature atwhich the air
column's length would be 1/2 its length at 0 Celsius.
- The temperature at which pressure
would be 0. (Note: The temperature at which this happens,
for an ideal gas, is called Absolute Zero).
Consider possible sources of error and
uncertainty in your experiment.
- How much uncertainty do you think
there is in your length readings for the air column, and how much effect
would this uncertainty have in the positions of the points on your graph?
How much uncertainty would you therefore expect in your estimate of the slope
of your graph, and then of the temperature at which pressure
would be 0?
- The bottle expands and contracts
as a result of temperature changes. How would this affect your graph,
and how would it affect your estimates?
- When you immerse the bottle in the water it is
subjected to water pressure, which for a flexible plastic
bottle tends to increase the air pressure in the bottle.
How much effect do you think this has on your results?
- Atmospheric pressure might vary
2-3% from day to day. What effect would this have on your
estimate of the temperature at which pressure would be zero?
- Atmospheric pressure at Abingdon's
600 meter elevation above sea level is significantly less than standard
atmospheric pressure. What effect would this have on your results?
- What other sources of error
and uncertainty are there in this experiment, and how much effect
do you think they might have on your final results?





