The figure below shows and actual stack of nine disk weights.

Each weight in the stack has a potential energy relative to the tabletop; since all weights are equal the potential energy of a given weight is proportional to its altitude, or to its position on the stack.

The figure below shows the same system, except with the top weight replaced by a weight at the level of the table.

• The new weight at the level of the table could be the weight which was previously at the top of the stack, or it could be the weight that was previously at the bottom of the stack and somehow got squeezed out.
• If the weight was formerly at the top of the stack, it might have gotten to table level by being pushed off, in which case its potential energy would have converted to kinetic just before it struck the table.
• If the weight was squeezed out of the stack, then it might well exit with a kinetic energy provided by the squeezing force.

In any event, we see that the potential energy of the system is now less than it was originally.

• The decrease in the potential energy of the system is equal to the former potential energy of the top weight.

If no energy is dissipated, then there should be an increase in kinetic energy equal to the loss of potential energy.

This kinetic energy increase could be any of the following:

We now consider a fluid in a uniform cylinder whose cross-sectional area is 8 cm^2.

• The depth of the fluid above an exit hole is 90 cm.
• We consider the top .5 cm layer of the water in the cylinder.

As water flows out, over some time `dt the .5 cm top layer will be replaced by an equal volume and mass of water flowing out of of the hole.

• The result will be a decrease in the potential energy of the system equal to the potential energy of this water layer relative to the hole.
• If no energy is dissipated, and if the water in the cylinder falls slowly enough that the kinetic energy of the water in the layer at the top of the column remains negligible, this potential energy decrease will be equal to the kinetic energy of the water flowing from the hole.
• We can therefore determine the velocity of the water flowing from the hole by finding the potential energy change of the 'stack', or column of water, as the water level decreases.

The potential energy change will be equal to the potential energy of the water layer we are considering. We find this potential energy easily enough.

• We can easily find the volume of the layer, from which we can find its mass and therefore its weight. From its weight and its altitude with respect to the hole we can find its potential energy with respect to hole.
• As shown in the figure below, the volume of the layer (which is a cylinder) will be the product of the 8 cm^2 area of its base and its .5 cm altitude, or 4 cm^2.
• At 1000 kg / m^3, this volume will have a mass of .004 kg.
• The weight of this mass is .003 kg * 9.8 m/s^2 = .0039 N.
• The potential energy associated with this weight at a height of .9 m is .035 J.

If there is no dissipation of energy, then conservation of energy tells us that `dKE + `dPE = 0.

• The kinetic energy change will therefore equal the .035 J PE loss.
• Setting the KE of the .004 kg exiting mass equal to .035 J, we easily solve for the velocity v of the exiting water.

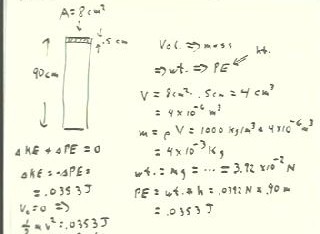
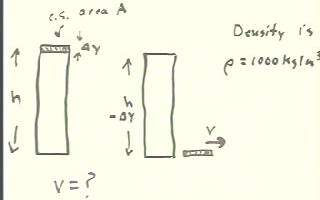
We now symbolize the numerical calculations we just made.

We follow the same order of calculations as before. As shown below:

• The volume of the layer will be V = A `dy.
• The mass of the layer will therefore be m = `rho V = `rho A `dy.
• The potential energy of the layer will thus be PE = weight * h = mg * h = (`rho A `dy) g * h.
• The change in potential energy will therefore be `dPE = - `rho A `dy g h.

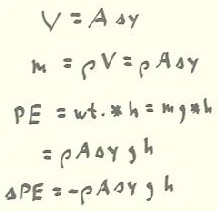
We apply conservation of energy to determine v:

• The kinetic energy change will be the negative of the potential energy change, or `dKE = `rho A `dy g h.
• Assuming that the initial velocity of the water in the layer is 0 (i.e., water isn't descending fast enough to give us a significant kinetic energy before exit), the change in kinetic energy will be equal to 1/2 m v^2, where v is the velocity of the exiting water.
• Since the mass of the exiting water is equal to the mass `rho V = `rho A `dy of the water layer it replaces, the kinetic energy change is as indicated in the third line from the bottom of the figure below.
• Setting this kinetic energy change equal to the negative of the potential energy change we obtain the equation in the second line from the bottom of the figure below.
• This equation is easily solved for v; we obtain v = `sqrt(2 g h).
• Note that this velocity is the same as the velocity that the water layer would have had if it had fallen the distance h, starting from rest. You should be sure you understand, in terms of energy conservation, why this is so.

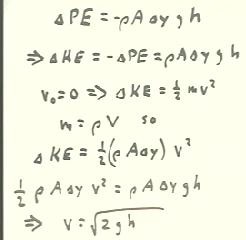
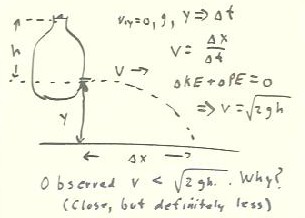
We easily determine from its projectile behavior the exit velocity of water from a container in which the depth above the exit hole is known. We then compare this exit velocity with the prediction we made from our energy analysis.

• We allow water to exit in the horizontal direction from a point y units above a level surface and measure the range `dx of the flow stream.
• From y we determine the time required for the stream to fall from the hole to the level surface, and from this time we easily determine the horizontal velocity of the stream, which we assume to be constant.
• From the measured water depth h relative to the hole we obtain our prediction for v ( we predict v= `sqrt(2 g h)).
• Our observed exit velocity v is close to the predicted exit velocity but is somewhat less than our prediction.
• We attempt to explain why the exit velocity seems to be less than the prediction.

Our prediction was based on several assumptions. You should review those assumptions and evaluate them for yourself.

• Probably the most significant difference between assumption and reality is the assumption that no energy was dissipated in the process.
• In many situations the primary mechanism of energy dissipation is friction.
• In the situation the water and the boundaries of the hole exert frictional forces on one another, slowing the water near the boundaries of the hole.
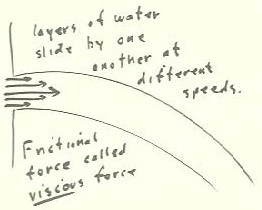
• The water further from the boundaries of a hole will move faster than the water at the boundaries.
• If we have a circular hole, we effectively have circular cylinders of water sliding by one another at difference speeds.
• If the hole is irregular, it should be clear that we still have layers of water sliding by one another a different speeds.
• As layers of water slide by one another, they exert frictional forces on one another, thereby dissipating energy.
• The frictional forces exerted by layers of fluid as they slide by one another are called viscous forces.
• The result of these viscous and other frictional forces is to increase the thermal energy of the water.