"
Physics II
Class Notes, 1/20/99
Today we see
- how Bernoulli's Equation expresses the potential and kinetic
energy relationships explored in the preceding class, and
how it also expresses the obvious relationship between pressure
and depth in a stationary fluid.
Bernoulli's equation is stated at the top of the figure below.
- It relates the velocity, altitude and pressure
of a fluid.
(In cases for the fluid is significantly compressible, `rho can also be a variable; for
the present we will be talking about water in situations were it is not significantly
compressible).
We note that the terms 1/2 `rho v^2 and `rho g h are
reminiscent of the expressions for kinetic and gravitational
potential energy.
- When we multiply the terms of the equation by volume,
we in fact obtain 1/2 mv^2 and m g h.
Multiplying pressure P by units of volume gives us
units of work, further confirming the analogy with conservation
of energy.
During the last class we determined that when water flows from a hole
in the side of a container, when water depth relative to the hole is h,
then if no energy is dissipated the exit velocity of the
water is found from energy conservation to be vExit = `sqrt(2 g
h).
We use Bernoulli's equation to obtain the same result:
We define state 1 to be the velocity, altitude
and pressure at the slowly descending water surface in
the container.
- the pressure is equal to that of the atmosphere,
the velocity of the fluid is approximately zero (the
fluid is descending slowly in the container, but we assume that the velocity of the fluid
is small compared to the exit velocity and is therefore negligible), and
the altitude is 17 cm, as measured from the position
of a hole.
- We say that P1 = 1 atm, h1 = 17 cm and v1 = 0.
We define state 2 to be the velocity, altitude
and pressure of the water as it exits the
container.
- the pressure is again atmospheric (the water doesn't
obtain its exit velocity until it is completely free of the container and therefore out in
the atmosphere),
the altitude is 0 and
the velocity is the unknown velocity vExit.
- We say that P2 = 1 atm, h2 = 0 and v2 =vExit.
Bernoulli's equation says that 1/2 `rho v^2 + `rho g h + P is constant,
which means that the value of this expression is the same for both
states.
We therefore write the equation at the bottom of the figure
below.

Since the pressures are equal, as indicated in the
second line of the figure below, the pressure terms can be subtracted from
both sides and thereby eliminated.
- The result is the equation in the third line, which relates velocity
and altitude for the two states we have defined.
We rearrange the equation so that the kinetic energy terms
are on one side and the potential energy terms on the
other.
- In this rearrangement we see (second line from bottom of figure) that the change
in the kinetic energy term is equal to the negative of
the change in the potential energy term, which is a direct
analogy to energy conservation in the absence of
energy dissipation.
- We see also that when pressure is constant the sum
of the kinetic and potential energy terms is constant,
as indicated in the line at the bottom of the figure below.
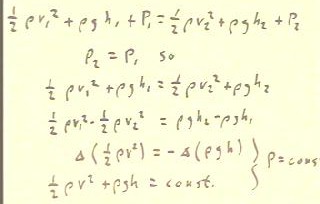
It follows that a decrease in the potential energy term
is associated with an increase in the kinetic energy term.
- We again note that if we multiply by the volume V of the fluid element, we obtain its
kinetic and potential energies so that the expression given that the bottom of the figure
below expresses energy conservation.
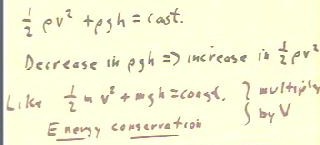
We can now solve for the exit velocity v2 the
equation relating the velocities and altitudes for the two states we have defined:
- We begin with the equation in the first line and divide both sides by
`rho.
- When we factor the 1/2 from the left-hand side
and the g from the right-hand side we obtain
the equation in the second line.
- Using the fact that the velocity v1 of the fluid in the first state is nearly
0, we obtain the equation in the third line.
- This equation is easily solved for v2, obtaining the expression in the
second line from the bottom.
- We finally note that h2 = 0, so that the exit velocity is
v2 = `sqrt( 2 g h1).
- We note that this is identical to the expression `sqrt(2 g h) obtained
by energy considerations in the preceding class for the exit
velocity, where h was the altitude of the fluid
relative to the hole and is easily identified with the h1 of
the present model.
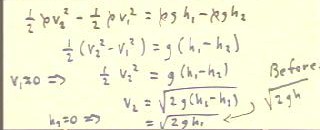
Though we haven't shown all the details, it is certainly plausible
that the constant-pressure form of Bernoulli's equation shown in the
first line below follows directly from energy conservation.
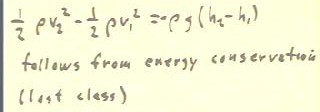
We now relate pressure P to the potential energy term
`rho g h.
If we consider a fluid filling a 'rectangular' container(called
a 'rectangular parallelopiped'), we see that the bottom of the container
must support the weight of all the fluid above
it.
- It follows that the pressure at the bottom of the container,
which is the force per unit area exerted on (and by) the fluid at this
position, is equal to the total weight of the water divided by
the area.
- The mass of the water is obtained by multiplying its density by
the volume of the water, and the weight is obtained by
multiplying this mass by the acceleration of gravity.
The volume of the container shown below is h * A.
We therefore see that the weight of the water is `rho A g h.
When we divide this weight by the area A,
the area divides out and we see that the pressure is
just `rho g h.
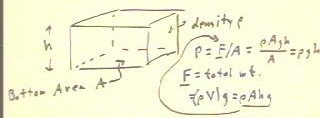
Bernoulli's Equation gives us the same result.
- We implicitly have assumed that the fluid is stationary in the
container.
- It follows that only the P and `rho g h terms are changing,
so that an increase in P is associated with a decrease in
`rho g h.
- This is consistent with our experience of fluids, in
which decreasing altitude (i.e., increasing depth) is associated with increasing
pressure.
- The various forms of Bernoulli's equation for constant
velocity are given that the bottom of the figure below.

Another application of Bernoulli's Equation is depicted below, where we see that increasing
velocity can be associated with decreasing pressure.
- If water is moving through a closed pipe which narrows at
a certain point, then assuming that the water fills the pipe, it should be clear that to
carry the same amount of flow its velocity must
be greater in the narrower part of the pipe.
- If the pipe is horizontal, then there is no significant
difference in the altitude h of the water from the wider to the
narrower section.
- It follows that the resulting increase in the kinetic energy term
1/2 `rho v^2 must be associated with a decrease in the pressure P.
We quantify the nature of the velocity change:
- Assuming that the velocity in each part of the pipe is uniform across
the entire cross-section of the pipe, we see that the distance the water
travels during a time interval `dt is v1 `dt in the larger pipe, and v2
`dt in the smaller, where v1 and v2 are implicitly assumed the the velocities in
these respective parts of the pipe.
- The volume of water flowing in each pipe during this time interval is
the volume of the water cylinder whose 'base' area is
the cross-sectional area of the pipe and whose 'height'
is the distance traveled by the water, as indicated in the figure.
- If the radius of the first pipe is r1 and that of the second is r2,
then the two volumes are V1 = `pi r1^2 (v1 `dt) and V2 = `pi r2^2
(v2 `dt), as indicated.
- Since the amount of water flowing through one part of the pipe in any
time interval is equal to that flowing through the other, these volumes
are equal.
- Setting the volumes equal we see that the ratio of velocities is the inverse
square of the ratio of the radii.
An equivalent way of saying all this is the 'continuity
equation' A1 v1 = A2 v2, expressing the relationship between flow velocity in
cross-sectional area.
This equation can be ranged to give us v2 / v1 = A1 / A2, as shown
below, and the resulting conclusions about the ratios of radii and/or
diameters..

"
