Bernoulli's Equation

Physics II

Class Notes, 1/22/99

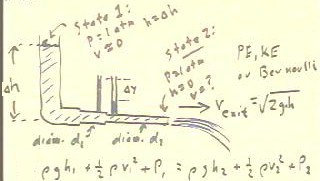
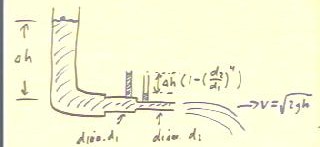
The sketch below depicts the apparatus used in Experiment 6.

The parameters to be analyzed include `dh, `dy, d1, d2, and vExit:

`dh stands for the depth of water in the large vertical tube, as measured in the vertical direction relative to the end of the horizontal outflow tube.
vExit is the velocity of the water as it exits the system, and should from either Bernoulli's's equation or from energy considerations the equal to `sqrt(2 g `dh), in the absence of dissipative forces.
d1 and d2 are the diameters of the horizontal tube before and after the tube changes diameter ('before' and 'after' have the obvious meanings in terms of the direction of the flow).
`dy is the difference in the water depth in the small vertical tubes before and after the horizontal tube narrows.

We will first analyze the state of the system, defined by the values of the parameters P, v and h, at two positions:

State 1 will be the state at the 'top' of the large vertical tube, at which point pressure P is 1 atmosphere, velocity v is approximately 0 and altitude h is `dh.
State 2 is the state at exit, where pressure is 1 atmosphere, velocity is v = vExit and altitude is zero.

The analysis of these two states is straightforward (see notes from preceding class), and we determine that v2 = vExit = `sqrt(2 g `dh).

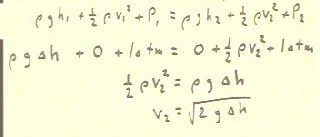
We will now analyze the state of the system before and after the tube narrows.

We begin by determining the theoretical velocities, based on our previous result for vExit.

If we let v1 be the velocity before and v2 the velocity after the tube narrows, the continuity equation tells us that the velocities are in inverse proportion to the cross-sectional areas of the tube before and after it narrows.
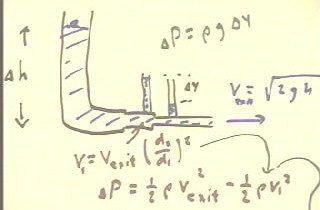
As shown below we see that v1 = (d2 / d1)^2 v2, with v2 = `sqrt(2 g `dh).

We will analyze the system at two new states:

State 1 will consist of the unknown pressure P1, the velocity v1 determined in the preceding figure, and the altitude h = 0 of the horizontal tube before narrowing.

(We assume that the diameter of the tube is small enough that altitude differences within a horizontal tube result in negligible pressure differences; h = 0 therefore indicates that the altitude is the same as that of the outflow position, as we would expect for a horizontal tube).

State 2 will consist of the unknown pressure P2, the velocity v2 = vExit and the altitude h = 0 in the horizontal tube after narrowing.

(We assume that the velocity of the water in this tube is the same as that of the exiting water, which will be the case if the diameter of the tube does not change before the water exits).

We wish to find the pressure difference `dP = P1 - P2 between state 2 and state 1.

We see that since h is constant, the sum of the kinetic energy and pressure terms will therefore be constant.
The lesser velocity of the water in the larger tube (or pipe, as it is referred to in the figure below) implies a greater pressure in that tube, so `dP will be positive.

The lesser velocity of the water in the larger tube (or pipe, as it is referred to in the figure below) therefore implies a greater pressure in that tube, so `dP = P1 - P2 will be positive.

The pressure difference will therefore be the difference in the kinetic energy terms of Bernoulli's equation, so

`dP = 1/2 `rho vExit^2 - 1/2 `rho v1^2.

Recalling that `dy is the difference in the water levels in the two small vertical tubes, where the water is stationary, we can conclude that the pressure difference due to the narrowing of the horizontal tube is `dP = `rho g `dy.

The height h of the water column in a vertical tube tells us that the pressure where it joins the horizontal tube is `rho g h greater than the atmospheric pressure at the top of the vertical tube.

Since the difference in the heights of the water columns is `dy, the difference in pressures is `dP = `rho g `dy.

The fact that the water in the second vertical tube is higher than that in the horizontal tube tells us that the pressure in the horizontal tube at that point is in fact greater than atmospheric pressure, contrary to the ideal assumptions we have made. This difference is in fact due to dissipative frictional forces in the tube.

If we set the two expressions for the pressure difference equal, we obtain the equation at the bottom of the figure below.

In the equation, we have replaced v1 with the expression vExit (d2 / d1) ^ 2.

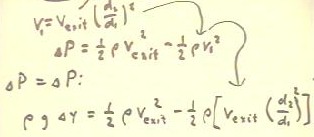
The preceding equation is repeated at the top of the figure below.

We solve the equation for `dy, as shown below, obtaining

`dy = `dh ( 1 - (d2 / d1) ^ 4 ).

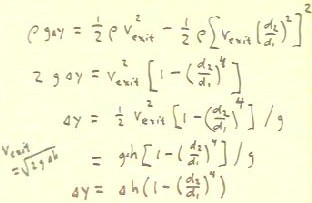
Our conclusion is that, assuming no dissipative frictional losses, the difference in the water levels in the small vertical tubes is related to the water level `dh in the large vertical tube by the above relationship, as indicated in the figure below.

We should be able to make observations of the quantities `dh, `dy, d1, d2 and vExit, or at least to observe quantities that will allow us to infer these values.

In one run of the experiment we obtained the information in the figure below.

The flow range information tells us that the water exiting the system in the horizontal direction had a range of 70 cm from a height of 70 cm. From this information we will be able to determine the actual velocity of the water and compare it with the ideal value.

The altitude `dh was difficult to observe in the custodian's closet; it should be easier in your kitchen.

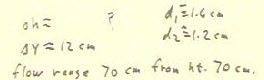
From `dy, d1 and d2 we easily determine `dh, obtaining an approximate value of `dh = 18 cm.

This value is consistent with the value we estimated, though without a lot of confidence, in the experiment.

Using this value of `dh, we find that the exit velocity should be v2 = 1.9 m/s, approx.

From the diameters of the tubes we determine that v1 = .55 v2 = 1 m/s, approx..
From the resulting difference in the kinetic energy terms, we conclude that the pressure difference across the narrowing should be approximately 1300 Pa.
This result is consistent with the pressure difference we would expect from `dy = 12 cm, which would result in a pressure difference of `rho g `dy = 1200 Pa (approx.).
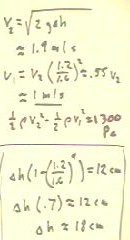