"
Physics II
Class Notes, 1/25/99
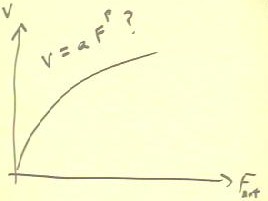
A plot of the average velocity vs. net force for the terminal
velocity experiment is shown below.
- Average velocities are obtained by dividing the distance
through which the marble moves by the time observed.
- The net force is the force in excess of
that required to just barely move the marble through the fluid.
- From the shape of the curve, and from theoretical considerations,
we expect that v = a * Fnet ^ p.
- We could use curve-fitting techniques to determine the most
appropriate value of p.
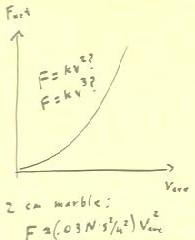
Below we reverse the variables to show Fnet vs. vAve.
- We think of this curve as indicating the net force exerted on the
marble as a function of its velocity.
- Assuming that the marble reaches a terminal velocity shortly after is released
from rest, we interpret this as an approximate graph of net
force vs. velocity.
Since the amount of water that must be disturbed in a given
time interval is proportional to the velocity of
the marble, and since the disturbed water will gain more velocity
for a faster marble than a slower, we expect that the force
required to move the marble through the water will be at least proportional
to the square, and perhaps to the cube of the velocity.
- Using DERIVE we find that F = k v^2 tends to give us a good
model for the data for each of the three groups performing the
experiment.
- However, for different groups using marbles of approximately the same
size we obtained different values of k.
- Our results showed that k was probably between .02 N s^2 / m^2 and .04
N s^2 / m^2 for a marble of diameter 2 cm.
- These results can be compared with results given in texts or tables in handbooks.
`00
We observe a soft drink bottle with an initial state where 300
ml of air are confined at a temperature of 298 K and
a pressure of 1atmosphere.
- A thin tube leads from a water reservoir in the bottom
of the bottle to a container at some height above the reservoir.
- When thermal energy is added to the gas in
the system, the pressure in the system will increase.
- As the pressure in the system increases, water
will be pushed up the tube.
- A sufficient pressure increase will transfer water to
the upper container, doing significant work as a result
of the added thermal energy.
- The rise of water in the tube can be seen as the direct result of
Bernoulli's equation, with the `rho g h increase of the
water in the tube balances the pressure increase at the water
surface in the bottle.
- The relationiship between the added thermal energy and
the work accomplished is the beginning of our study of thermodynamics.

To raise the water to height `dh above
the water surface in the bottle requires that the gas achieve a sufficient
temperature to supply the required pressure.
- The water at the top of the tube is at atmospheric
pressure.
- The difference in `rho g h between water surface and
the top of the tube is `rho g `dh.
- The pressure at the water surface must therefore be `rho
g `dh greater than at the top of the tube.
- So the pressure at the water surface is 1 atm
+ `rho g `dh.
- If the tubing is thin enough, an insignificant
volume of water will be required to fill the tube and
the volume of the gas in the container will therefore not
change significantly.
- We conclude that, for a thin tube and a well sealed container,
V and n remain constant within the system while pressure rises
from 1 atmosphere to 1 atmosphere + `rho g h.
- The Ideal Gas Law tells us that for constant V and n,
temperature is proportional to pressure.
- We therefore conclude the temperature required is T = (1 atm +
`rho g h) / (1 atm) * 298 K.

`01
Since the system, originally at 298 K, was immersed in water at a temperature of 70
Celsius = 343 K, we assume that the temperature of the gas rose to near 343 K.
- The pressure therefore should have increased by the
same factor as the temperature, a factor of 1.15.
- The pressure in the heated system should therefore
have been 1.15 atm.
We estimated the height which the column was raised
to be approximately 2 m.
- The difference in `rho g h corresponding to a 2
meter water column is easily found to be 20 kPa, or about .2
atm.
- From this estimate of the column height we see that the pressure in the
heated system should have been about 1.2 atm.
A more accurate estimate of the height of the water column was in fact
approximately 1.5 m, which would agree perfectly with
the observed temperatures of the system.
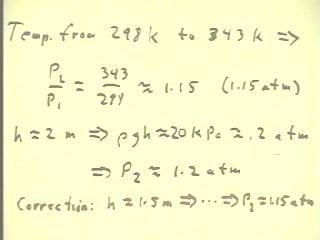
`02
"
