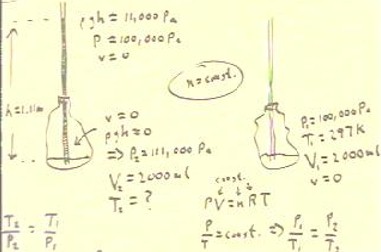
If the system depicted in the picture at left in the figure below consists of 2000 ml of air, supporting a column of water 1.11 meters high, then assuming that the system started at atmospheric pressure and 25 Celsius, what must be the temperature of the gas inside the bottle?

• Using Bernoulli's's equation, a comparison of the state at the open end of the tube and at the surface of the water in the bottle shows us that the pressure in the bottle must be 11,000 Pa higher than atmospheric pressure, or approximately 111,000 Pa.
• Since we assume that the tube is very narrow, with negligible volume, we see that the volume of the system is unchanging.
• Since the system is sealed from the outside, no gas can enter or leave and we therefore see that the number of moles n is constant.
• We therefore conclude from the ideal gas law PV = nRT that P / T = n R / V must be constant, so that P1 / T1 = P2 / T2.
• Since we know both of the pressures P2 and P1 for the two states of the system, and the temperature T1 of the original state of the system, we can easily find T2.

To find T2 we invert the relationship P1 / T1 = P2 / T2 and plug in the appropriate quantities.

• We see that the temperature of the system must be 57 C.

If the system is now raised to a temperature of 80 C = 353 K, with the water at the 1.11 meter level permitted to flow out of the tube and into a reservoir that height, the gas will expand and the water flowing out of the tube is that displaced by the expansion.

• Since the height of the water in the open end of the tube remains constant, the pressure of the gas remains constant.
• Since air is blocked by water and therefore cannot bubble out through the tube, it is clear that the number n of moles of air in the system remains constant.
• We therefore conclude that only temperature T and volume V will change.
• Intuitively we see that the ratio of volumes will be the same is the ratio 353 / 330 of temperatures during the expansion.
• We easily conclude that V2 / T2 = V1 / T1, where now state 1 is the 'old' state 2, with pressure 1.11 kPa, volume 2000 ml and temperature 330 K and state 2 is the state when temperature has reached 353 K.
• Since we know V1, T1 and T2, we can easily solve for V2.
• We find that the volume of the system ends up at 2140 ml.
• The system will have therefore expanded by 140 ml, and 140 ml of water will have been displaced to the higher reservoir.

We note that work has been done by this thermal engine, since 140 ml water has been raised to a height of 1.11 meters above its original level.

We wish to see how much thermal energy was transferred to the system to accomplish this.

The thermal energy increase of the system is the amount of thermal energy added to increase the temperature of the gas.

For a diatomic gas, such is the nitrogen or the oxygen that makes up most of the air around us (and in our system), the ideal values of Cv and Cp are 5/2 R and 7/2 R.

• The additional energy required for a diatomic gas is the energy required to spin the dumbbell-shaped gas molecules end-over-end; this energy is not needed for monatomic gasses.

From these molar specific heats we will be able to determine the amount of thermal energy required to raise the temperature of the gas in the system.

We can use our system to raise water to any height, up to the maximum possible height dictated by the initial and final temperatures 297 K and 353 K of the system.

• If we raise water to near the maximum height, we will have to 'use up' most of our available temperature difference to increase the pressure of the system at constant volume in order to get the water to this height, and there will be very little temperature difference left to expand the gas; as a result very little water will be raised and not much useful work will get done.
• If we raise the water only a little, very little of the available temperature difference will be required to increase the pressure at constant volume and get the water up the tube, leaving a lot of temperature difference available to expand the gas; as a result a lot of water will be raised but since it is raised not very far not much useful work will get done.
• Somewhere between the extremes of raising the water just a little and raising it almost as much as possible, there is a height to which we can raise the water to maximize the useful work obtained from the system.

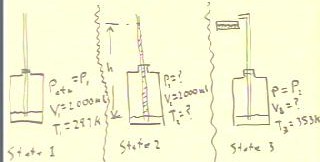
To determine the work done by the system we first find the volume of the water raised:

• For a given altitude h, as we have seen in calculations done to this point, we use Bernoulli's equation to determine the pressure P2 in state 2.
• From the pressure P2 we determine the temperature T2, using the known pressures P1 and T1.
• Then using the maximum temperature, T3, we use our knowledge of V2 and T2 to find the final volume of the system.
• From the initial and final volumes we find the change in the volume of the system.

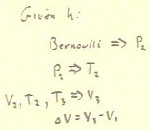
When applying Bernoulli's equation in state 2, we distinguish between the state of the gas and the state of the water by using A and B for the states of the water, used in Bernoulli's equation. Otherwise we might become confused between state 1 and state 2 of the gas and the two states of the water.

Looking at state 2, we let B be the state of the water at the open end of the tube and A the state at the surface of the water in the bottle.

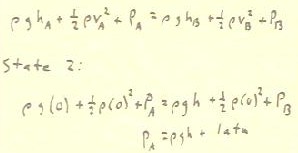
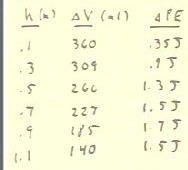
Following through the process we determine for various heights h the volume changes `dV indicated below.

From each height and volume change we can then determine the associated potential energy change.

• The results are shown in the table.
• We see that of the specified heights, the greatest potential energy change occurs when we raise the water to a height of .9 meters.

It is not difficult to determine the amount of thermal energy required to raise the n moles of gas from the initial to the final temperature:

The system in state 1 consisted of 2000 ml = .002 m^3 of diatomic gas at 297 K and pressure 100,000 Pa.

• From PV = n R T we see that the number of moles is n = P V / (R T), which for the conditions of state one tells us that there are approximately .08 moles of gas in the system.
• For every height there is a temperature at which the system changes from constant volume to constant pressure.
• Knowing this transition temperature, the amount of thermal energy transferred is found by using Cv as the molar specific heat between original temperature and transition temperature, then Cp between the transition temperature and the final temperature of the system.
• To obtain a rough estimate of thermal energy required, we assume that for the .9 meter height the transition temperature is about halfway between the initial and final temperatures, so the we can use an average of Cv and Cp as our approximate molar specific heat.
• For diatomic gas this average is approximately 25 J / mol K. Thus the energy required to heat the .08 moles from 297 K to 353 K, a change of 56 K, is about (25 J / (mol K) ) * .08 moles * 56 K = 110 Joules (approx.).
• We see that we have obtained 1.7 J of useful work from an input of 110 Joules of thermal energy.
• This implies an efficiency of 1.7 / 110, or about 1.6%.