"
Physics II
Class Notes, 1/29/99
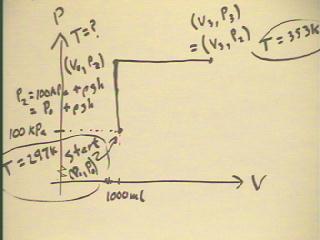
The figure below depicts the pressure vs. volume graph
for the bottle engine as water first rises in the tube as the pressure
increases at constant volume, then as the gas expands at constant pressure as water is
forced out at a constant altitude.
- The system starts at temperature 297 K, and at some
unspecified volume V0 and pressure P0 = 100 kPa (approx),
and ends up at temperature 353 K.
- As water rises to altitude h, pressure must increase
by `rho g h.
- From the pressure ratio between the first and second states we can
easily determine the temperature of the second state.
- The volume ratio between the third and second
state will be the same as the temperature ratio between
the states.
Video File #01
During the first part of the cycle, thermal energy flows
into the system as the pressure increases at constant
volume; the required thermal energy is found using the molar specific
heat at constant volume.
During the second part of cycle, thermal energy flows
into the system at constant pressure; the required
thermal energy is found using the molar specific heat at constant
pressure.
If the system returns to its original state so that another
cycle can perform more work, the net work done
by the cycle will be the area enclosed by the pressure vs. volume
curve.
Thermal energy might be added to the system or taken
from the system as it returns to its original state; the net result, though, will
be a transfer of thermal energy out of the system as it cools
to its original temperature.
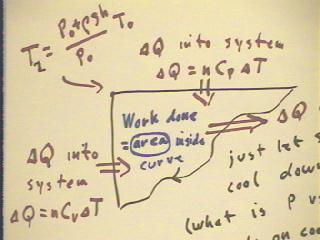
We could just remove the system from the heat source and
let it cool down, though this would take some time.
We could if we wanted to run the cycle more quickly release the excess
pressure by opening a valve.
We could even find a way to let the gas expand slowly while keeping it
at a constant temperature until it reached its original pressure,
then let it cool down.
The net thermal energy put into the system and taken out thus depends
on how we return it to its original state.

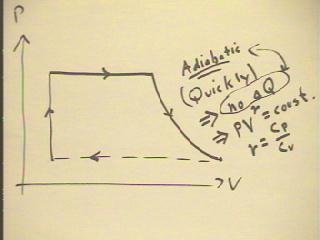
A common way of lowering pressure is to release it by
opening a valve.
- This typically releases the pressure so quickly
that there is no time for any thermal energy exchange during
the expansion.
- A process in which there is no thermal energy exchange is called adiabatic.
- In an adiabatic process, P V^`gamma remains constant,
where `gamma is the ratio Cp / Cv of specific sheets at
constant pressure and constant volume.
Video File #02
Another way of releasing the pressure, which is generally
impractical but is of interest for theoretical reasons, is to
allow the gas to expand slowly while adding thermal energy to
maintain the constant temperature.
- Such a process is called isothermal.
- In such a process thermal energy is clearly added from
the heat source.
- Since the temperature of the gas remains constant,
none of the thermal energy added goes into the internal energy of
the gas, rather all goes into the work done by the expansion of
the gas.

Video File #03
To increase the temperature of a gas, we require thermal
energy 1/2 n R `dT to increase the kinetic energy in
each of the three independent directions of motion
in space, and we require an equal amount for each
of the independent directions in which the molecules might gain rotational
kinetic energy.
- The three directions of motion in space are generally
referred to as the x, y and z directions.
- For diatomic molecules, there are two independent directions perpendicular
to the axis of the molecule about which the molecule can rotate with significant kinetic
energy.
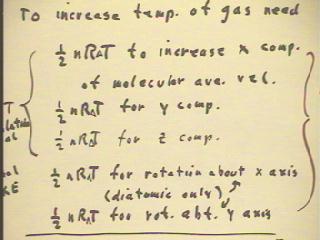
The total energy the goes into the molecules is
called the internal energy of a system.
- We call the energy that goes into motion in the x, y and z
directions the translational kinetic energy of the system.
- For a predominantly diatomic gas such as air, which consists of over
90% Nitrogen and Oxygen (both diatomic), there are two more degrees of freedom,
the rotational degrees of freedom.
- Thus for a diatomic gas at temperature T we have internal
thermal energy 5/2 n R T.
If we wish to expand a gas at constant pressure we
must add another 2/2 n R `dT.
- Thus for a diatomic gas to change temperature by `dT requires thermal
energy 7/2 n R `dT.
- We thus say that constant-volume specific heat of a diatomic gas is 5/2
R, and the constant-pressure specific heat is 7/2 R.

The figure below summarizes where thermal energy goes into a system
consisting of a fixed number of particles of a diatomic or
a monatomic gas at constant pressure or constant
volume.
- The first term, 3/2 n R `dT, is required to change the translational kinetic energy of
the gas particles, which happens for any gas.
- The second term, 2/2 n R `dT, is required to increase the rotational kinetic energy if
the gas is diatomic.
- The third term, 2/2 n R `dT, is required to perform the work of expansion if the thermal
energy is added at constant pressure.
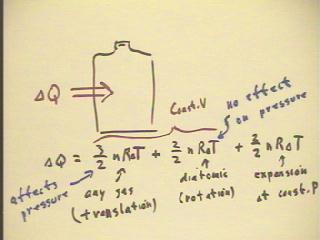
In an adiabatic process, P V^`gamma remains constant.
- For an ideal diatomic gas, Cv = 5/2 R and Cp =
7/2 R so `gamma = 1.4.
- For an ideal monatomic gas, Cv = 3/2 R and Cp
= 5/2 R so `gamma = 1.67.
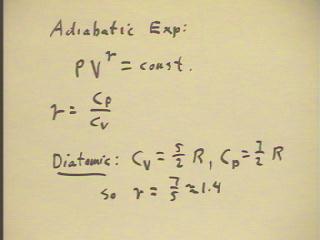
Video File #04
The figure below once again shows the complete cycle for the bottle
engine, with an adiabatic expansion.
- The pressure P3 and volume V3 at the beginning
of the adiabatic process are known in terms of the initial
pressure P0 and the height h to which water is raised.
- From the values of P3 and V3 we can easily find the value of the
constant: P V^`gamma = const.
- It will then follow that P = const. / V^`gamma, and we can accurately
plot the curve corresponding to the adiabatic expansion.
- The work done by the gas during the adiabatic expansion is the area
beneath the curve representing the adiabatic process; from this
curve the area and hence the work can be estimated.
- Students with a calculus background will understand that the indicated
integral is the accurate expression for the work.
The integral is easily evaluated.

Video File #05
"
