"
Physics II
Class Notes, 2/05/99
By observing a pulse moving down a 20 m string and
back, we see that the more tension we put into the string the faster
the pulse travels.
By synchronizing the round trip of a pulse in
a string of length 20 m, under different tensions from 5
N to 20 N, with the period of a pendulum, we
obtain the data indicated below for pendulum length L vs.
string tension T.
- We observe that a doubling of tension is associated
with a halving of pendulum length; recalling that pendulum
period is inversely proportional to the square root of
pendulum length, we reason that the time required for
the pulse to travel the 40 meters is inversely proportional to
the square root of the tension.
- From this it follows that the velocity of the pulse must be proportional
to the square root of the tension.
- This result is predicted theoretically by the Impulse-Momentum
Theorem.
- We determine the time `dt required for the pendulum to
complete its cycle in each case, recalling that the angular
frequency of the pendulum in radians/second is `sqrt(g /
L).
Using these results we infer the pulse velocities
in the table below.

The velocity of a pulse in a string is
theoretically given by v = `sqrt( T / `mu), where 'mu
is the mass per unit length of the string.
- Note that in the figure below L stands for the length of the string and
not the length of the pendulum used in the experiment,
which is merely a timing device and whose properties have nothing else to
do with the properties of the string.
- The quantity `mu is easily calculated from the mass
and the length of a sample of the string.
- The velocities predicted by this formula for the given string are as indicated
in the figure below.
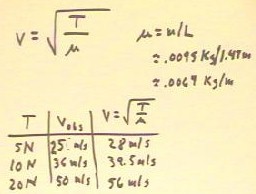
Measuring the time required for a fundamental cycle of
the fixed 20 m string, we determine that for the 5 N tension a
complete cycle requires 1.8 seconds.
- This complete cycle corresponds to the time required for
a full cycle of a sine wave to travel 40 meters,
double the length of the string.
- The fundamental mode of vibration of the string,
depicted in the figure below, occurs when the reflected half-cycle of the
wave meets the opposite half-cycle as it travels in the
opposite direction down the string.
- Since the cycle requires 1.8 sec, the 1/2
cycle that corresponds to the time required for the wave to
travel the 20 m length of the string is .9 s, implying a
wave velocity of 22 m/s.
- We therefore have a predicted wave velocity of 28 m/s,
an observed pulse velocity of 25 m/s, and and observed wave
velocity of 22 m/s.
- These quantities should theoretically be equal, since
each corresponds to the velocity of a disturbance traveling
in the string.

"
