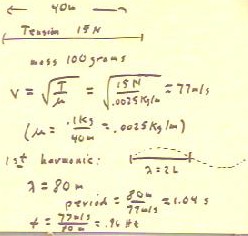Your work on this assignment is excellent. You communicate well, your reasoning is correct and you use a good variety of images.

 We wish to find the natural periods and frequencies associated with a 40 m string whose mass is 100 grams, under a tension of 15 N, with both ends fixed.

• We begin by calculating the velocity of a pulse in the string, as indicated below.
• The fundamental mode of vibration, or the first harmonic, fits the length of the string as indicated.
• The wavelength of the first harmonic is therefore double the length of the string.
• In this case the wavelength is 80 meters.

• At 77 m/s, it requires 1.04 s for a pulse to travel this .
• The waveform will therefore repeat every 1.04 s, and the period will be 1.04 seconds.

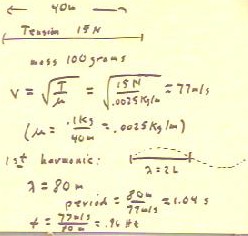
We can visualize the period and frequency relationships as shown in the two figures below.

In the first figure we have labeled a wavelength and indicated it by a double arrow.

• We have also indicated the distance v * 1 sec traveled by the wave in a second.
• The period is the time required for a pulse to travel one wavelength.
• For the picture below, the wavelength is greater than the distance traveled in a second, so that the time required to travel the wavelength will be greater than 1 second.
• To find the number of seconds we will therefore divide the wavelength by the distance traveled in the second.

In the second figure we see that the length of a cycle is greater than the distance traveled in a second.

• It follows that there will be less than a complete cycle in a second.
• We therefore divide the (shorter) distance in a second by the length of the cycle in order to get the number of cycles per second.

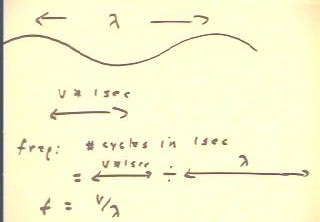
You should repeat this reasoning, and sketch the appropriate figures, for a wavelength that is less than the distance traveled in a second.

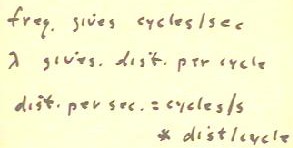
The second harmonic of our wave occurs when the entire wave 'fits' the string.

• In this case the wavelength is equal to the length of the string, and we have a 40 m wavelength with a pulse moving at 77 meters/second.
• We can see therefore that 77/40 of a cycle will pass a given point in a second.
• We calculate the frequency to be 1.93 Hz.

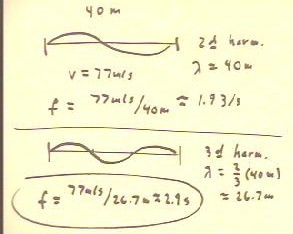
We could similarly calculate the frequency of the third harmonic, for which three half-waves fit the string.

• The wavelength would be 2/3 the length of the string, or 26.7 m.
• The frequency would therefore be f = 77 m/s / 26.7 m = 2.9 Hz.

The table below shows the frequency in Hz vs. the number of the harmonic.

• We see that the frequencies are the fundamental, double the fundamental and triple the fundamental.
• For waves in a string, the number of half-cycles always increases by 1 as we move from one harmonic to the next.
• You should see the relationship between this pattern and the pattern of frequencies.

In Josh's experiment, where a string was disturbed with increasing frequencies, the first three harmonics were clearly observed and had the indicated periods, as shown in the table above.

• The uncertainty in each period is approximately +- .02 sec.
• The associated frequencies are as indicated.
• We see that the frequencies of the first two overtones are in fact double and triple the fundamental frequency.

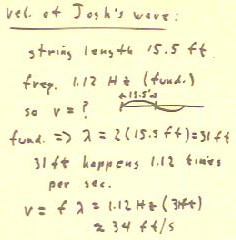
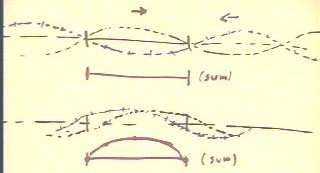
We sketch the pair of waves that form the fundamental mode of vibration of the string.

In the second picture each pulse has moved in its respective direction a distance of approximately 1/4 the length of the string.

• The reflected wave is sketched in blue, and has small 'tic marks' to distinguish it from the first.
• The pulses in this case reinforce one another, and their sum is as indicated.

When the pulses have moved another 1/4 of the length of the string, they will meet as indicated in the first picture below and cancel.

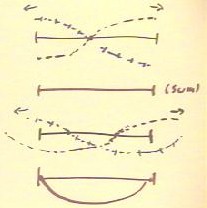
The shape of the string will therefore repeatedly pass through the indicated configurations in sequence, creating the familiar shape of the fundamental mode of vibration indicated at the bottom of the figure.