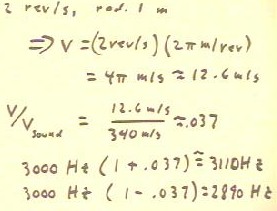"
Physics II
Class Notes, 2/10/99
We wish to find the Doppler shift associated with a 3000 Hz
buzzer swung at two revolutions per second around a circle
of radius one meter.
- We first estimate the Doppler shift as if it was proportional to
the ratio of the velocity of the buzzer to
that of sound.
- This estimate is reasonably accurate whenever the speed of the source
is much less than that of sound.
- We need to find the velocity of the buzzer as it approaches
and as it recedes from the observer.
- The distance around
the circle is 2 `pi r = 2 `pi meters, which is covered twice
per second, so that the buzzer is moving at 2 *
2 `pi m/s = 12.6 m/s (approximately).
- Assuming that sound moves at 340 meters/second, we see
that the buzzer is moving at .037 times the speed
of sound.
- Our approximation is therefore that when the buzzer approaches its
frequency increases by proportion .037 and when it recedes
the frequency decreases by the same proportion.
Note that this is not completely accurate, as we will see.
- The approximate frequencies are therefore as calculated in the figure
below.
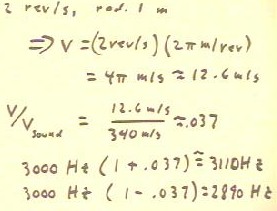
To obtain the accurate frequencies we can proceed numerically as
in the example below.
- We find that in .01 second the buzzer emits 30
cycles.
- During this time it moves .125 meters closer to the observer.
- The sound emitted at the last instant of the .01 seconds therefore
travels .125 meters less than the sound emitted at the very
beginning of the .01 seconds.
- This difference in time implies that the sound emitted at the end
of the time interval takes .00037 seconds less to get to the
observer than the sound emitted at the beginning of the time interval.

We therefore conclude that the observer hears all 30 cycles in
.00963 seconds, which implies a frequency of approximately 3110
Hz, as shown in the top half of the figure below.
In the bottom half of the figure we derive a general expression for the
time required for sound to travel the distance that the source travels
and time `dt.
- The source travels distance vs * `dt, where vs
stands for the speed of the source.
- The sound takes time vs * `dt / vSound to travel the same
distance.

During time `dt the source emits f * `dt
cycles, where f is the frequency of the source.
- The observer will therefore hear the f * `dt cycles in time (`dt
- vs `dt / vSound).
- The frequency heard by the observer will be f'
= #of cycles heard / time in which the cycles were heard.
- It follows that the observer hears the frequency indicated
in the last two lines of the figure below.
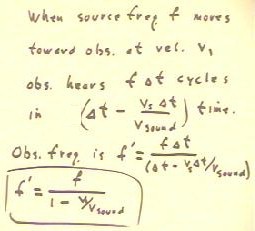
The actual frequencies heard should therefore be as indicated in the
figure below.
- Note how the ratio .037 of source velocity to sound
velocity appears in the expressions.
- Comparing with the frequency estimates made earlier,
we see that there is a small difference but that it would require more
than the 2-decimal-place precision of our calculations to determine.
- Note the important relationship between the comparisons made
below and the approximations 1 / (1 +- `epsilon) = 1 -+ `epsilon (i.e.,
the relationship the tells us why 1 / .99 is about 1.01).
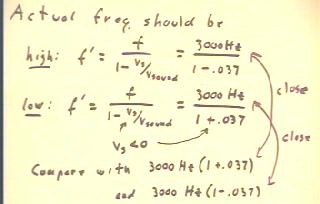
The situation in which the observer approaches the source can
be analyzed in a somewhat similar way.
- In this case, in .01 seconds the last sound the
observer would hear would have been emitted (.01 seconds + .01 sec * vo /
vSound) = .01 sec (1 + vo / vSound) earlier than the first sound heard
during the interval, where vo is the velocity of the observer.
- In terms of an arbitrary time interval `dt, the sounds heard by
the observer during time `dt would have been emitted by
the source during the time interval `dt (1 + vo / vSound).
- The number of cycles heard by the observer with therefore be 1
+ v0 / vSound times as many as emitted during time `dt.
- The frequency heard by the observer will thus be f' = f (1 + vo
/ vSound).
Another interesting situation, which we will not pursue here,
is that in which the observer, source and the air
are all moving.
"