A .9 m metal rod in which longitudinal pulses travel with velocity 6000 m/s, supported by a magnetic field or in free fall so that its vibrations are not damped, will vibrat in such a way that the free endpoints will be antinodes.

• Between any two antinodes there must be a node, and for any situation (such as this one) where the velocity of a pulse is constant the node-antinode distance will be uniform.
• The fundamental mode of vibration will therefore have a node-antinode distance of .45 m, as indicated.
• Since the wavelength is equal to 4 node-antinode distances, we see that the wavelength of the fundamental mode must therefore be 1.8 m.
• The frequency corresponding to this wavelength is easily calculated.

By contrast, if one end of the rod is constrained to remain stationary while the other end is free, the entire length of the rod can consist of a node-antinode distance and the fundamental wavelength will therefore be 3.6 meters.

• It follows that if we allow the  rod to vibrate in response to transverse disturbances, with a pulse velocity of 600 m/s, then the fundamental frequency will be f0 = 600 m/s / 3.6 m = 166.7 Hz.

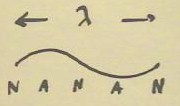
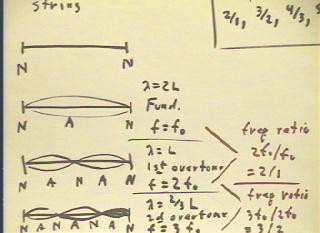
For a string fixed at both ends, both ends will be nodes and the fundamental mode of vibration will consist of these two nodes with an antinode in the middle of the string.

• For this fundamental mode of vibration, the node-antinode distance is 1/2 the length L of the string and hence the wavelength of the fundamental will be 4 * (1/2 L) = 2 L.
• The fundamental frequency will be f0 = v / (2 L).

The first overtone, or the second harmonic, will consist of four node-antinode pairs so that the wavelength will be equal to the length of the string.

• The frequency of this overtone, which has half the wavelength of the fundamental, will therefore be double the frequency of the fundamental.
• We note that the frequency ratio from the first to the second overtone is therefore 2/1.

The next overtone must contain an additional node-antinode pair, so that the string contains 6 node-antinode distances and the wavelength is therefore 2/3 L, which is 1/3 that of the fundamental.

• The frequency of this overtone must therefore be 3 times that of the fundamental.
• The frequency ratio between the first and second overtones is therefore 3/2.

This pattern continues, adding a node-antinode pair for every subsequent harmonic.

• The natural frequency ratios of a string are therefore found to be 2/1, 3/2, 4/3, 5/4, 6/5, etc..
• The frequency ratio of harmonic # n+1 to that of harmonic # n is therefore f(n+1) / f(n) = (n+1) / n.

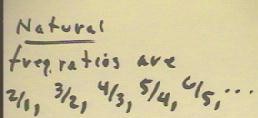
The ratios for a vibrating rod or air column for which one end is a node and the other an antinode can be easily found to be 3/1, 5/3, 7/5, etc..

• These ratios can be found in a vibrating string, with the 3/1 ratio being the ratio between the third harmonic and the fundamental, and the 5/3 ratio found between the fifth and third harmonics.

On a keyboard, a doubling of frequency (an 'octave'), is achieved in 12 steps, with each key (white or black) having a frequency r = 2^(1/12) = 1.05946 (approx.) higher than the one to its left.

• For example, the natural 5/4 = 1.25 ratio is approximated by four of these 'steps', which gives us the ratio 1.05946 ^ 4 = 1.26 (approx.).
• This ratio corresponds to an interval of a 'major third', in music terminology.
• The 3/2 and 4/3 ratios are approximated very closely by the 7th and 5th powers of 2^(1/2), and correspond to the intervals of a 'perfect fifth' and a 'perfect fourth' in music terminology.
• The 6/5 ratio is also approximated, this time by the 3d power of the fundamental ratio, and corresponds to the interval of a 'minor third'.
• All these intervals, when heard, have sounds that we tend to find pleasing and 'harmonic'; we can identify any of these intervals with a familiar tune.
• The interval obtained by 'splitting' the 12-interval octave into two equal ratios of 1.05946^6 generally do not sound pleasing or 'harmonic'. This interval is called a 'tritone', and does not approximate any natural mode of vibration with which we are generally familiar. We therefore say that the tritone is an 'unnatural' interval.