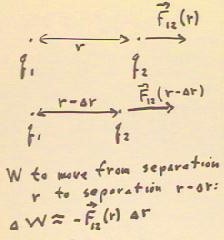
Coulomb's Law, has we have seen in experiments, relates the force between point charges to the distance separating them.
As we have already seen, we can use Coulomb's Law to determine the work done when two charges move closer or further from one another:
The total work done if we change the separation from a to b is approximated by adding up the `dW contributions over short intervals `dr.
In the limit we obtain the integral indicated in the figure below. For non-calculus students, this integral is just a way of very accurately summing up the work contributions over very short distance intervals.
We define the potential function V(r) as the work per unit charge to move a test charge from infinite distance to distance r.
The potential is the precise sum (calculus: the integral) of all the F `dr = -k q / r^2 `dr contributions, from an infinite distance to distance r, using an integral.
The electrostatic potential V(r) at a point is thus V(r) = k q / r.
- This is as it should be, because if we move a positive test charge closer to a positive charge q, we must do work on it and its potential energy increases. Therefore it electrostatic potential, defined as its potential energy per unit charge, becomes greater.
The potential difference from point A at distance a to point B at distance b is simply the difference `dV in the values of the potential function V at the two points. That is, `dV = V(b) - V(a) = k q / b - k q / a.
In the figure below we determine the potential difference from the point A and a distance of 120 cm from a positive charge point of 8 * 10^-8 C, to point B at a distance of 80 cm from this charge.
The figure below depicts a system of 3 charges. We wish to find the net force on the 7 `microC charge.
We use the usual procedures, as shown below, to determine the x and y components of the force F21.
We then use similar procedures to determine the x and y components of the force F31.
We total the x and of the y components of the 2 vectors to obtain the x and the y components of the resultant vector.
We can easily determine the energy of this system.
We imagine assembling the system one charge at a time, starting with a system in which no charges are present.
- We assume that q1 is brought in from a great, essentially infinite, distance.
- Since q1 ends up at point A, which is a distance r12 = `sqrt(.65) m from q2, the electrostatic potential at A will be VA = k q2 / r12.
- Since the electrostatic potential VA is the work per unit charge required to bring a charge from infinite distance to position A, we see that the potential energy of charge q1 at this position must be PE21 = q1 VA = k q1 q2 / r12.
- If we evaluate VA we see that is approximately 75,000 volts.
- PE21 is therefore equal to 75,000 volts * 7 `microC = .53 J.
The third stage of the assembly consists of bringing the charge q3 from a great distance to the indicated point.
The total potential energy is therefore as indicated in the figure below.
We see that the total energy of the system is negative.
"