more electric fields, Gauss' Law

Physics II

Class Notes, 4/04/99

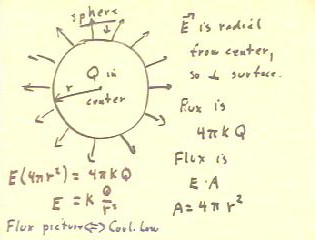
The flux picture of electric field uses the fact, which is proved from Coulomb's Law the Divergence Theorem of multivariate calculus, that the flux of a charge Q is 4 `pi k Q.

More specifically, the flux through any closed surface enclosing total charge Q must therefore be 4 `pi k Q.

If the enclosing surface and the distribution of the enclosed charges have an appropriate shared symmetry, then the electric field might have uniform strength over the surface and, furthermore, the electric field might be perpendicular to the surface at every point of the surface.

For example, we have seen how the field of a point charge is uniform in strength over any sphere concentric with the charge, and how the field is also perpendicular to the sphere at every point.

In such a situation, the magnitude of the flux through the surface will simply be the product of the electric field E at the surface and the area A of the surface.

The flux will be positive if the electric field vectors are directed out of the surface and negative if the electric field vectors are directed inward through the surface.

In the figure below electric field vectors are directed out of the surface so the flux is positive.

The total flux of the charge Q is 4 `pi k Q.
Another expression for the total flux is E * A = E * 4 `pi r².
Setting the two expressions for the total flux equal we see that E = k Q / r², as we would expect from Coulomb's Law.
This shows that Coulomb's Law follows from the flux picture.

We can also easily obtain the flux picture from Coulomb's Law, so that the flux picture is equivalent to Coulomb's Law.

Video Clip #03

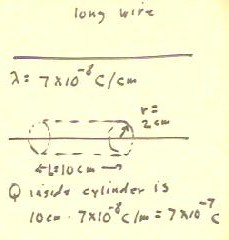
If we now consider a very long straight wire which carries a uniform charge `lambda = 7 * 10^-8 C / cm (i.e., every cm of the wire contains a uniformly distributed charge of 7 * 10^-8 C), we can use the flux picture to determine electric field at any point near the wire.

By a symmetry argument, which we will complete below, we wil conclude that the electric field lines must always be perpendicular to the wire, and that they must be radially symmetric about the wire.

The symmetry argument will be completed shortly.

For the time being we note that, if the ends of the wire were suddenly switched, we would still have a very long wire with the same uniform charge density, which would not change its electric field.

We note also that if the wire was rotated about its axis through any angle, the charge density would not be changed so that the electric field would still remain unchanged.

The electric field will therefore pass at a perpendicular through the curved surface of any cylinder whose axis coincides with the wire, and must have uniform magnitude everywhere on this curved surface.

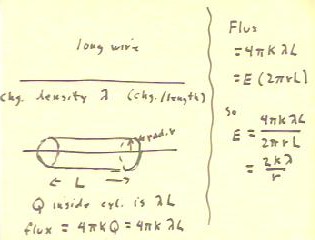
If we construct a cylinder of radius r = 2 cm and length L = 10 cm, with its axis along the wire, then the cylinder will enclose charge Q = 7 * 10^-7 C, as indicated below.

The total electrostatic flux through the cylinder will therefore be as indicated in the second line below.

Since the flux is also equal to E * A, and since the area of the curved surface of the cylinder is 2 `pi r L = .0125 m², we see that the flux is E * .0125 m².
Setting the two expressions for the flux equal we obtain E = 61,600 N / C. (the? In the figure below indicates that you should verify this unverified calculation.)

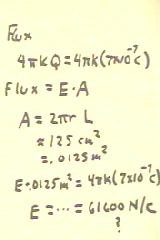
Video Clip #04

In general if we have a long straight wire with uniform charge density `lambda, as indicated in the figure below, then at a point much nearer the wire than the end of the wire the symmetry of the situation is as stated above:

Recall that the electric field must remain unchanged if the ends of the wire are switched.
If any point electric field coming from the wire is not perpendicular to the wire, then it must be 'tilted' either to the 'right' or the 'left' at that point. Since switching the ends of the wire would reverse this 'tilt', this field would contradict the assumption of symmetry.

Recall also that the previously mentioned rotation of the wire about its axis has no effect on its electric field.

If we look at an 'end view' of the wire we see that, if at any point the field does not make the same angle with the radial line than any other, this lack of symmetry will follow the system through any such rotation. This contradicts our conclusion that rotation has no effect on the electric field.

If all field vectors make the same nonzero angle with the radial line, then reversing the ends of the wire will reverse this uniform angle, again contradicting the assumption of symmetry.

We therefore conclude that the electric field of the wire, except at points much nearer the ends of the wire than to the wire, must be perpendicular to the wire and radially symmetric. We might visualize the electric field lines coming out of the wire as bristles on a long cylindrical brush.

If we construct a cylinder of radius r and length L, with axis parallel to the wire, it follows the electric field passes through the curved surface of the cylinder at angle perpendicular to the surface, and that the field is uniform over the surface.

The area of the curved surface is 2 `pi r L.
The electrostatic flux through the surface will therefore be E * A = E * 2 `pi r L.
The cylinder encloses charge `lambda L, so the total flux is equal to 4 `pi r L.
Setting the two expressions for flux equal, we obtain an equation we can solve for E.

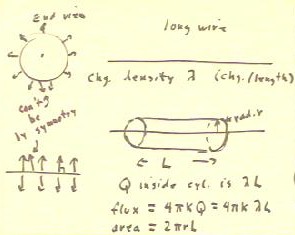
At the right of the figure below we solve the equation to determine that E = 2 k `lambda / r.

Video Clip #05

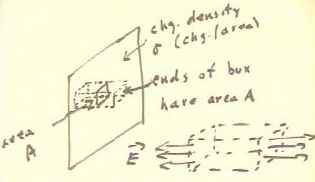
Consider now a large plane area over which is uniformly distributed a charge with density `sigma, the charge per unit area (measured in units of C / m²).

If the plane is rotated about an axis through its center and perpendicular to the plane, we will still have a large plane area with the same uniform charge density.
From this it follows that the electric field must at every point be perpendicular to the plane, since any location where the field was not perpendicular would be changed under such rotation.
This holds for any point much nearer the plane than to its edges.

We construct a rectangular surface perpendicular to the plane, with cross-sectional area A in the plane.

This surface encloses a charge `sigma * A, so the electrostatic flux through the surface must be 4 `pi Q A `sigma.

Since the flux is perpendicular to the plane, penetrate the surface only at its ends, which have total area 2 A.

Setting the two expressions for the flux equal, we obtain at the top of the figure below, which we solve for E.

We see that the electric field in the vicinity of a large plane with uniform charge density is E = 2 `pi k `sigma.
Note that this field does not depend on the distance from the plane.

Comparing with the expressions k q / r² for a point charge, 2 `lambda / r for a line charge and 2 `pi k `sigma for a plane charge, we see that the dependence on distance is inverse square for a point charge, inverse first power for a line charge, and independent (i.e., zeroth power) for a plane charge.

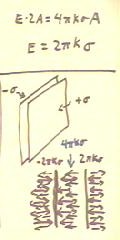
In the figure above we have two opposing plates, one with uniform charge density `sigma and the other with uniform charge density - `sigma.

We assume that distance between the plates is much less than the separation of the plates, so that almost any point between the plates will be much closer to the plates then to their edges.
Except near the edges of the system, a uniform electric field 2 `pi k `sigma will emanate from the positively charged plate, while a uniform electric field -2 `pi k `sigma will emanate from the negatively charged plate.
Between the plates these fields will reinforce to give a field of magnitude 4 `pi k `sigma, while outside the plates these fields will cancel.

This system is called a capacitor. We will look at the voltage between the plates and its relationship to the charge on and area of the plates in our next class.

Video Clip #06