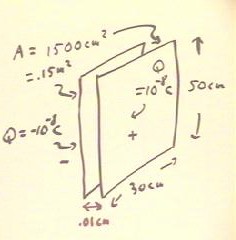
We analyze a capacitor consisting of two parallel plates, each 50 cm by 30 cm and uniformly separated by .01 cm.

• We assume a charge of +- 10^-8 C on the two plates.

The charge density will tell us the electric field strength, which with the separation of the plates will tell us the voltage between the plates, from which with the charge on the plates we can determine the capacitance of the system.

• The charge density, 6.7 * 10^-7 C / m², is found in the first line by dividing the charge of the plates by the area of the plates.
• In the second line we find the electric field to be 7.4 * 10⁴ N / C.
• In the next three lines we determine the voltage, both symbolically and numerically.

• The 7.4 * 10⁴ N / C electric field and the .01 cm distance gives us a 7.4 N m / C = 7.4 J / C = 7.4 V potential difference between the plates.

• The capacitance is found symbolically and numerically.
• Numerically, the 10^-8 C charge corresponding to the 7.4 V potential difference gives us a capacitance of 1.4 * 10^-9 C / V = 1.4 * 10^-9 F.

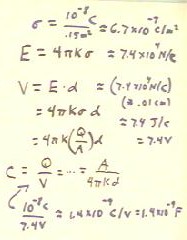
Video Clip #01

We can explain how a voltmeter measuring the voltage across a capacitor shows a voltage which keeps increasing, but at a decreasing rate.

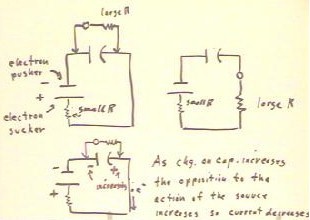
In the figure below we depict, on the left-hand side of the figure, a circuit consisting of a capacitor in series with a voltage source. In parallel with the capacitor we have a voltmeter, which consists of a coil in a magnetic field and a  large resistance.

• The negative terminal of the source repels, or 'pushes away' electrons while the positive terminal 'pulls' electrons toward it. As a result, electrons will be pulled from the positive plate of the capacitor and pushed to the negative plate.
• As this process continues the charges on the capacitor plates continue to build, but the increasing voltage across the capacitor opposes the voltage of the source, tending to push and pull electrons in the direction opposite to that of the source.
• This increasing voltage is read on the voltmeter.
• As a voltage read on the meter increases, the net voltage around the circuit decreases and the current through the circuit therefore decreases.
• The current in the circuit tells us how fast charge is built on the capacitor.
• Thus as the voltage indicated on the meter increases, the voltage will increase at a decreasing rate.

Video Clip #02

The figure at upper right in the figure above depicts a voltmeter connected in parallel with a capacitor.

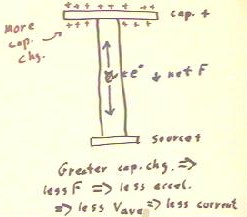
The figure below depicts an electron in a wire connecting a source and a capacitor. The circuit is assumed to be complete.

• We assume that the charge in the capacitor fairly small, so that the voltage of the capacitor is considerably less than that of the source.
• The electron is attracted to the positive terminal of the capacitor and to the positive terminal of the source, but since the source voltage is higher than that of the capacitor the net force on the electron is toward the source.

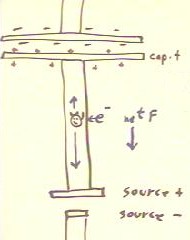
As charge builds on the capacitor, an electron in the wire will be more and more strongly attracted to the capacitor and will therefore experience a smaller and smaller net force toward the source.

• The result is that for greater capacitor charge the electrons in the wire drift more and more slowly toward the source, and current in the circuit therefore decreases.

Video Clip #03

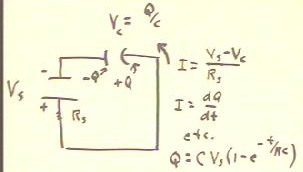
In a series circuit consisting of a source with a small resistance and a capacitor, the voltage across the capacitor is related to the charge on the capacitor by V_C = Q / C.

• The current in the circuit is equal to the net voltage divided by the resistance of the circuit.
• The net voltage is the difference between the source and the capacitor voltage, so the current is (V_S - V_C) / R.