The Bohr Model of the Hydrogen Atom

Physics II Notes 4/16/99

The Bohr Model of the Hydrogen Atom

If we model the hydrogen atom as an orbital system with an electron orbit in the (much more massive) proton in a circular orbit, with the centripetal acceleration provided by the Coulomb force between the two unlike charges, we obtain the relationship between orbital velocity v and orbital radius r. If we assume that the angular momentum of the orbiting electron is quantized by the relationship m v r = n h / (2 `pi), where h is Planck's constant 6.64 * 10^-34 J s, we avoid the conclusion that the electron almost instantly dissipates all its energy in the form of electromagnetic radiation and we obtain a model that explains the spectra observed in discharging hydrogen. Solving the two resulting equations in v and r, we conclude that orbital radii of approximately rn = n^2 * .529 Angstroms are possible, with corresponding orbital velocities near vn = 1/n * (2 * 10^6 m/s). When an electron 'falls' from some allowed orbit to one with smaller radius its potential energy decreases and its kinetic energy increases, with a decrease in total energy. Energy is conserved by the emission of a photon with an associated frequency f = - `dE / h.

Just as a satellite can orbit a planet, with the centripetal acceleration supplied by the gravitational attraction between the planet and the satellite, we can think of an electron orbiting a proton, with the centripetal acceleration supplied by the electrostatic attraction between the charges.

In both cases the system actually orbits its center of mass. In the case of a planet and a small satellite, the planet is so much more massive than the satellite that the center of mass effectively coincides with the center of the planet.
The same is more or less true of an electron orbiting a proton.

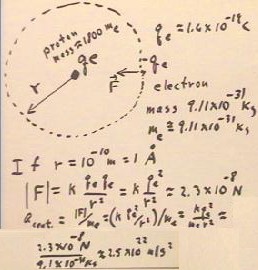
The proton has about 1800 times the mass of an electron (consult the tables in your book for the actual masses).

For many applications we can assume that the center of mass of the system coincides with the proton, though for high-precision measurements and predictions the difference becomes significant.

The electron does not actually orbit the proton in the manner of a satellite around a planet, but this model still gives us very good predictions.

The situation is depicted below.

The electron orbits the proton at distance r.
The force F in the figure below is the only force acting on the electron, and has magnitude F = k q_e * q_p / r^2; since the proton and electron have equal charges this can be written as F = k q_e^2 / r^2.
The resulting acceleration is a_cent = F / m_e = k q_e^2 / (m_e r^2).
For an orbit of radius 10^-10 m, on the order of the radius of a typical atom, this acceleration would be 2.5 * 10^22 m/s^2--an incredibly high acceleration.

We note here that an accelerating electric charge will emit electromagnetic radiation, so that according to classical electromagnetism we would expect that the electron would emit a great deal of high-energy radiation, at the expense of its kinetic energy.

That this does not happen will lead us to some of the basic assumptions of quantum mechanics.

Video Clip #01

In general we can set the electrostatic force F / m_e = k q_e^2 / m_e r^2 equal to the centripetal acceleration v^2 / r.

We solve the resulting equation for v to find that

v = `sqrt( k / (m_e r) ) * q_e = `sqrt( k q_e^2 / m_e) * [ 1 / `sqrt(r) ].
Thus orbital velocity is inversely proportional to the square root of orbital radius, just as with the orbit of a satellite about a planet.

The proportionality constant `sqrt( k q_e^2 / m_e) is easily evaluated. Its approximate value is 1.6 * 10^1 m^(3/2) / s.

For r = 10^-10 m, 1 / `sqrt(r) = 10^-5 m^(1/2), and we find v to be 1.6 * 10^6 m/s.
This is very fast; since the electron would with this velocity (1600 km / sec) in a circle of radius 10^-10 m, it would make a very large number of revolutions every second.

Video Clip #02

This sort of motion would almost instantly dissipate the orbital KE of the electron in the form of electromagnetic radiation.

If, however, we assume that the angular momentum I `omega of the electron is quantized, taking only integer multiples of h / (2 `pi), the electron will no longer be predicted to dissipate its energy in a continuous stream of electromagnetic radiation.

Since when a point mass m moves at velocity v in a circle of radius r its angular momentum I `omega is equal to m v r, we have the condition on angular momentum as indicated in the figure below.

We can solve this condition simultaneously with the velocity proportionality we derived above by setting centriipetal force equal to the Coulomb force.
The solution gives us r in terms of the multiple n of the angular momentum h / 2 `pi, as indicated in the last line of the figure.

Evaluating the quantity in brackets, we see that the radius of the orbit will be approximately n^2 * .529 Angstroms (an Angstrom is 10^-10 m).

As n increases from 1 to 2 to 3, etc., the radius of the orbit thus increases from 1 * .529 Angstrom to 4 * .529 Angstrom to 9 * .529 Angstrom, etc., increasing faster and faster.

The corresponding velocity is easily found to be approximately v = 1/n * (2 * 10^6 m/s).

We see that the velocity is inversely proportional to n.

Video Clip #03

For a given n, we thus have a specified orbital radius r and velocity v.

We therefore have a specific PE and KE, and hence a specific total energy, for the orbit.
The PE is negative and the KE positive. It will turn out that the magnitude of the PE is twice that of the KE, so that the total energy is negative and equal to half the PE.
When an electron 'falls' from one possible orbital state to another, moving closer to the proton, the magnituce of its PE increases so its (negative) PE decreases.
To conserve energy, a photon is emitted. This photon carries the energy -`dE lost in the 'fall'.
The light corresponding to such photons will have characteristics of a wave with frequency f = -`dE / h.

Video Clip #04