Alignment of Magnetic Dipoles

Physics II, 4/23/99

Alignment of Magnetic Dipoles

Magnets have been observed to occur only as dipoles, with North and South poles separated by some more or less fixed distance. The response of the magnetic dipole to an external magnetic field is to experience a torque tending to align the axis of the dipole with the magnetic field. This torque can be expressed as `tau = `mu * B * sin(`theta), where `mu is a property of the dipole called the dipole moment, B the external field strength and `theta the angle between the axis of the dipole and the magnetic field. An atom will have a magnetic field, which can be understood to some extent by analogy with the magnetic field that arises from a current loop. By the same analogy we can understand that such an atom will have the tendency to align itself with an external magnetic field. Atoms in a substance tend to be randomly aligned, due to the random thermal motion of the atoms, but in the presence of an external magnetic field the atoms may tend to align themselves in the direction of the external field, thereby enhancing the strength of the magnetic field within the substance.

The figure below depicts a bar magnet with a North and South pole between the poles of a much larger magnet.

The direction of the magnetic field is indicated by the red vectors.
The North pole of the bar magnet experiences a force in the direction of the magnetic field, and the South pole of the bar magnet experiences a force opposite to the direction of the magnetic field.
The net result of these two forces will be a rotational torque on the bar magnet, tending to rotate the magnet in the counterclockwise direction.

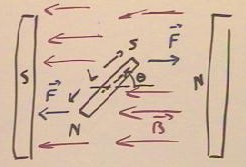
If the length of the bar magnet is L and the angle its axis makes with the magnetic field is `theta, then the torque on each pole of the magnet will be -L / 2 sin(`theta) * F.

The total torque will therefore be `tau = - L sin(`theta) * F.

If the bar magnet becomes stronger, the force F and therefore the torque will become greater.

A greater magnetic field will also result in a greater torque.
For a given bar magnet and a given magnetic field B, the angle `theta is 90 degrees the torque will be maximized.

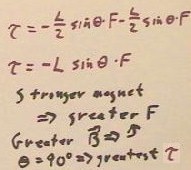
The force F will be proportional to the magnetic field B; the proportionality constant depends on the strength of the bar magnet.

The torque at the `theta = 90 deg position, simply being L * F, will thus also be proportional to the magnetic field, with another proportionality constant which also depends on the strength of the bar magnet.
We thus define the 'magnetic moment' of the bar magnet to be this proportionality constant, and designate it by the Greek letter `mu.
Thus, for the `theta = 90 deg position, we have torque `tau = `mu * B.

`mu is simply the constant by which we multiply the magnetic field to get the torque at the 90 deg position.

To get the torque at any other angular position, we simply multiply this maximal torque by sin(`theta), obtaining

torque = `mu * B * sin(`theta).

Again, the magnetic moment is a property of the bar magnet.

When multiplied by the magnetic field B and the 'angle correction factor' sin(`theta), the magnetic moment gives us the torque on the bar magnet.

More generally, we call the bar magnet a 'magnetic dipole'.

This term reflects the fact that the bar magnet has two poles, a North and a South pole.
Whenever magnets have been observed, they has been observed as dipoles, with both North and South poles.
Isolated North or South poles have not been observed. The reason for this is a mystery--according to our theories there is nothing to prevent such magnetic monopoles.

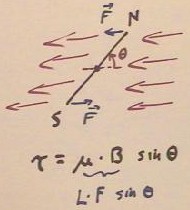
Video Clip #01

As we have seen a current loop creates a magnetic field perpendicular to the plane of loop.

Thus we would expect an orbiting electron to create a magnetic field.
Due to the force on the current, we also expect the loop to align itself to an external magnetic field, so that the two magnetic fields become more nearly parallel. In the absence of any other forces, the two fields would align completely.

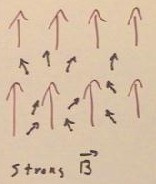
The figure below represents a bunch of atoms with the magnetic fields which result from the current loops in the individual atoms aligned randomly.

Due to the thermal motion of atoms in a substance, the alignment of magnetic fields will in fact tend to be random.

In the presence of a strong enough external magnetic field, there will be a measurable tendency of the magnetic fields of the individual atoms to align themselves with that field.

The alignment won't be perfect, again due to the random thermal motion of the atoms, but it will tend to reinforce and strength in the external field in the material.

Video Clip #02

Video Clip #03