Time Dilation; Source of Magnetic Field Revisited

Physics II, 4/30/99

Time Dilation; Source of Magnetic Field Revisited

Time Dilation

By considering a light beam bouncing between two mirrors, we show that if the speed of light is constant in all reference frames, then the time interval between reflections will be greater in a reference frame moving with respect to the mirrors than in a reference frame which is stationary with respect to the mirrors. We obtain a time dilation factor 1 / `sqrt( 1 - v^2 / c^2). We observe that a length contraction occurs, with a factor that is the reciprocal of the time dilation factor; that mass increases by the same factor as the time; and that simultaneity is not conserved between reference frames for events which occur at different places.

Source of Magnetic Field Revisited

By analogy with the expression for the electric field `dE = k `dq / r^2 of a charge `dq, we see the magnetic field `dB = k' I `dL / r^2 sin(`theta) of a wire segment of length `dL carrying current I as the result of the source I `dL, reduced from its 'perpendicular-direction value' k' I `dL / r^2 by factor sin(`theta). We use this expression to find the magnetic field at the center of a wire loop.

Time Dilation

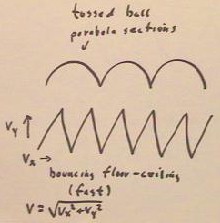
If you observe someone moving past you at a constant velocity vx, tossing a ball straight up and down as perceived from her frame of reference, then the ball will appear to you to move in a series of parabolic arcs, as indicated at the top of the figure below.

If on the other hand the ball is bouncing elastically from the floor to the ceiling of the vehicle in which the individual is riding, and bouncing at a high speed so that its speed is pretty much unchanging, then the path will be more of a sawtooth shape, as indicated in the figure.

If the vertical velocity of the ball has constant magnitude vy, then you will observe a ball velocity that is the vector some of the vertical velocity vy and horizontal velocity vx.

You will therefore conclude that the speed of the ball, as you observe it, is v = `sqrt( vx^2 + vy^2).

Suppose now that you are in a rocket ship lost in space someplace, and another ship comes flying by you at a constant velocity vx in the x direction.

Suppose that the individual in this ship is bouncing a light beam from floor to ceiling and back, repeatedly, between two mirrors.
Every time the beam is detected at the ceiling, an electronic signal is emitted from that position.

If the vertical distance between floor and ceiling is d, then you will observe the path from floor to ceiling then from ceiling to floor to follow a sawtooth pattern and to have some length s > d.

If `dt' is the time you detected between signals and v = c is the speed of the light beam, then you will observe that v = 2 s / `dt'.
If `dt is the time detected between signals on the other ship, where the light beam travels distance d from floor to ceiling or from ceiling to floor, then the time detected between signals on that ship is related to the velocity of the light beam by v = 2 d / `dt.

Video Clip #01

A fundamental assumption of physics is that the laws of physics are the same as observed from any frame of reference.

Since Maxwell's Equations, which predict the speed of light, express laws of physics, then the speed of light would therefore be the same as observed from any frame of reference.
This means that the speed of light must be the same as observed from within the passing ship as from your ship.
If this is the case then v = 2 d / `dt must be the same as v = 2 s / `dt'.
Since the distance d is different than the distance s, the time interval `dt as detected on the passing ship must be different than the time interval `dt' detected on your ship.

We compare the distances s and d.

If a beep is emitted every time the beam striked the floor, then the dimensions of one 'tooth' of the sawtooth pattern will be d units in the y direction and v `dt' in the x direction.
As observed from the lab the time `dt between beeps is simply `dt = 2 d / c.

The distance along the light beam from floor to ceiling, as measured from your ship, is thus the hypotenuse of a right triangle whose legs are .5 v `dt' and d.

Thus the distance s is `sqrt( d^2 + (.5 v `dt' ) ^ 2 ), and the round-trip distances double this.
At speed v = c we see that the time required, as measured from your ship is as indicated in the bottom line of the figure below.

The distance along the light beam from floor to ceiling, as measured from your ship, is thus the hypotenuse of a right triangle whose legs are .5 v `dt' and d.

Thus the distance s is `sqrt( d^2 + (.5 v `dt' ) ^ 2 ), and the round-trip distance is double this.
At speed v = c we see that the time required, as measured from your ship, is as indicated in the bottom line of the figure below.

We can solve the resulting equation for `dt'.

We find that `dt' = `dt / `sqrt( 1 - v^2 / c^2)--the time you measure is 1 / `sqrt(1 - v^2 / c^2) times as long as that measured on the passing ship.
This factor is equal to 1 for v = 0 and > 1 for v > 0.

Thus for any nonzero speed v, `dt' will be greater than `dt by the 'time dilation' factor 1 / `sqrt( 1 - v^2 / c^2).

Video Clip #02

Below we show a table of `dt' vs. v. As v -> c, `dt' becomes a larger and larger multiple of `dt, without limit.

Thus the time you measure between beeps will get longer and longer as the velocity of the passing ship increases.
You will thus observe the clocks on the moving ship to run more slowly than the clocks on your ship.

It also follows that the length of the passing ship will appear shorter to you than to the occupants of that ship. The 'length contraction' factor is simply `sqrt( 1 - v^2 / c^2).

The mass of the ship, as measured by the force you observe to accelerate it at a given rate, will also increase as the relative speed of the ship increases. The mass increase factor is the same as the time dilation factor.

The simultaneity of events will also be affected. Events occuring at different locations that accurate detectors on the passing ship show to be simultaneous will not be simultaneous as measured by accurate detectors operated from your ship.

Video Clip #03

Source of Magnetic Field Revisited

The figure below depicts a short segment of wire, of length `dL, carrying a current I. The point P lies at distance r from the segment, and in a direction perpendicular to the segment. The distance r is much greater than the length `dL of the segment.

The magnetic field at P, due to the segment, is `dB = k' I `dL / r^2, where k' = 10^-7 Tesla / (amp meter).

This expression is analogous to that for the electric `dE = k `dq / r^2 due to a point charge dq at distance r. Rather than the source `dq of the electric field, the source of the magnetic field is I `dL.
The direction of the magnetic field is perpendicular to both that of the current I and the vector r from the segment to the point P, and is found using the right-hand rule, crossing the vector I L into the vector r.

If the point P lies along a vector originating at the segment, with the vector making angle `theta with the segment, then `dB will be as before, but with the 'correction factor' sin(`theta) reducing its magnitude.

For a circular loop of radius r carrying a current I, the field at the center of the loop is easily found.

The direction to the center from each point on the wire is perpendicular to the loop, so any small length `dL will contribute k' I `dL / r^2 to the total field.
Each contribution `dB = k' I `dL / r^2 has the same I and r, so the sum of all the contributions is k' I / r^2 * sum (`dL).
The sum of all the `dL contributions is just the circumference 2 `pi r of the circle, so the total of the `dB contributions is k' I / r^2 * (2 `pi r) = 2 k' I / r.
By the right-hand rule if the current is counterclockwise, as depicted, the magnetic field of each contribution is vertically upward at the center of the loop. The total field is therefore vertically upward at the center.

Video Clip #04