http://vhmthphy.vhcc.edu/ > General Information > Request Access Code
temp vs t in bottle
mixing water
spec heats?
flow thru longer or shorter tubes
Diameter of the hole in the side of the container is 1/4 inch, which can be approximated as .64 cm.
Inner diameter of the larger tube is 3/16 inch, approximately .47 cm.
Inner diameter of the smallest tube is 1/8 inch, approximately .32 cm.
flow range
thermal energy in monatomic and diatomic gases
emergence of v2/v1 ratios etc. in gas law
Temp of Mixture
Heat a 50 ml sample of water, originally at room temperature, in the microwave for 10 seconds.
Observe the temperature of that sample for about 10 minutes.
Mix the two 50 ml samples. During the minute it takes for the thermometer to come to equilibrium, estimate what the temperature of the mixture should be.
Measure the temperature of the mixture again, then measure it over the next 10 minutes.
Estimate what the temperature was at the instant of mixing.
Graph temperature vs. clock time for the 50 ml sample you heated up, then for the 100 ml of combined water.
This will give you a total of 4 graphs. You can put them all on the same set of coordinate axes if you wish--in fact that would be desirable.
For each temperature vs. clock time curve, measure the slope at four different clock times, spread over the entire range of measurements. Get four slopes, in degrees per minute.
Make a table of rate of temp. change vs. temperature difference (temperature relative to room temperature)
For geometrically similar regions of space (like the regions of space occupied by the water, which are more or less geometrically similar), we have
(V2 / V1) = (A2 / A1)^(3/2) and
(A2 / A1) = (V2 / V1)^(2/3).
We saw in our notes why this is the case for a cube, and the result carries over to all geometrically similar regions, because they can be subdivided into an equal number of tiny cubes and the result applies to each.
Energy is gained or lost thru the surface, i.e., thru the area.
So at the same temperature, we expect that a sample with twice the volume will have 2^(2/3) = 1.6 times the surface area and will lose energy at about 1.6 time the rate.
The sample with twice the volume needs to lose twice as much energy to achieve the same temperature change as the first.
So at the same temperature we expect the second sample to change temperature at 1.6 / 2 times the rate, or .8 times the rate.
How well do our data validate this?

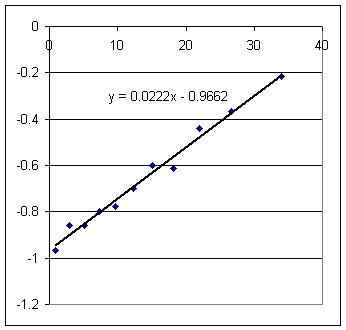
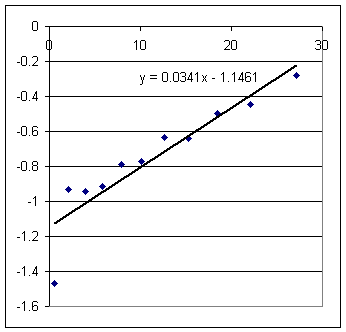
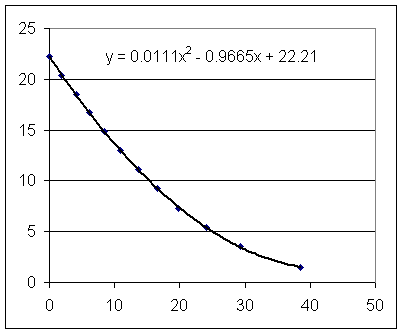
Figure out pressure difference and velocity for y2 = 5 cm, using the functions given in the graphs above.
Somebody submit a copy of the TIMER screen(s), along with tube lengths and group name (East or West).
I'll post it tonight to the Physics 202 access site 19-19-125
How much thermal energy did it take to bring the ice up to the temperature at which equilibrium between water and ice was first established?
How much of this thermal energy was required to bring the melted water to the equilibrium temperature, assuming that melting occurs at 0 Celsius?
Use all the evidence you have available to you, and figure out how much uncertainty there is in your final result.
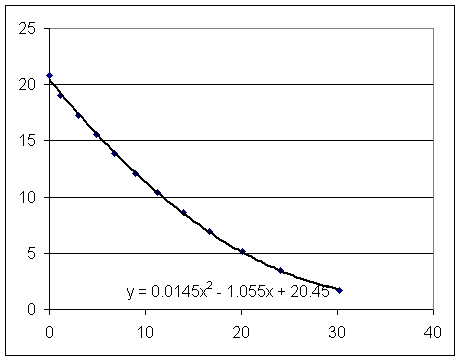
Estimate from the graph the surface velocity of the long-tube setup at t = 10 sec.
Estimate from the appropriate graph the clock time at which the short-tube setup has the same surface velocity.
Estimate the two corresponding depths.
Find the pressure difference.
Find the common velocity of the water in the tube.
Using the function v = .029 t - 1.055 to get the surface velocity of the long-tube setup at t = 10 sec.
Using v = .0222 t - .967 find the clock time at which the short-tube setup has the same surface velocity.
Using y = .0145 t^2 - 1.055 t + 20.5 and y = .0111 t^2 - .957 t + 22.2 find the two corresponding depths.
Find the pressure difference.
Find the common velocity of the water in the tube.
The bottles have been pressurized by sealing the pressure release valve, bringing them in from the cold and allowing them to come into thermal equilibrium with the air in the room. The vertical tube has been maintained in a vertical position.
The water level in the vertical tube is between 50 and 75 cm above the water level in the container.
Each container contains about 2 liters of air.
Pressure columns in the tubes are 20-30 cm long.
What is the pressure in your bottle?
If the vertical tube is bent at the 35 cm level above the water level, what pressure will we achieve in the system?
If the pressure equalized gradually, allowing the system to remain at nearly constant temperature, what will be the resulting volume change of the system?
How far will the liquid in the pressure-indicating tube move?
If the pressure is equalized suddenly, what will happen to the volume and temperature of the system?
How will heights of the water columns in the two systems compare and why?
How will rigidity of container affect heights?
How will difference in volume affect heights?
At 10 cm height, how much will temp. have increased?
When water has raised 10 cm, gonna drain it back to original height.
How will volume of exiting water differ?
How will exit velocity vs. clock time differ?
Univ Phy beats and harmonic oscillations
What are the lengths of the chains?
For each setup:
What was the observed frequency of the 'long' chain?
What was the beat frequency?
Given mass density 6.4 grams / 21 cm, figure out for each observed tension what should have been the frequency of the fundamental mode .