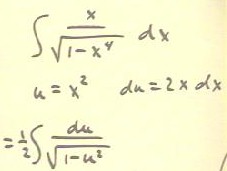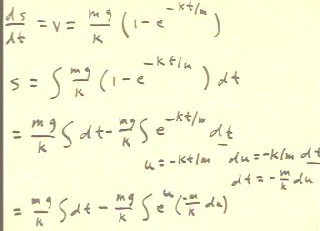integration by substitution, integration by parts

Calculus II

Class Notes, 1/22/99

A Differential Equation

We wish to find h(t) = s for a velocity function v(t) = m g / k ( 1 - e^(-kt/m) ) for an object dropped from altitude h0.

Note that since the factor in parentheses is a pure number, m g / k must have units of velocity; note also that since k t / m is a pure number, the reciprocal of k / m must have units of time.

We set up the differential equation ds / dt = mg / k ( 1 - e^(-kt / m) ), as shown below.
We integrate the equation to find s, using the substitution u = -kt / m, as shown below.

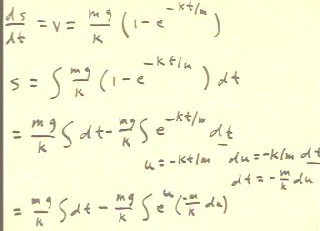
Substituting for u, we obtain the function s = h(t) shown in the third line below.
We evaluate c using the initial condition h(0) = h0.
We obtain c = h0 - m^2 g / k^2, which can be seen to have units of distance.
We substitute this value of c into the solution to obtain the expression for h(t) in the last line below.

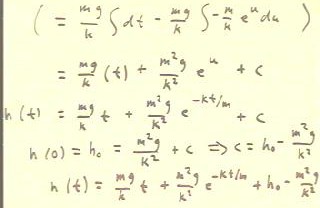
Some Strategies for Substitution

To integrate the expression below, we are certainly inclined to make the substitution u = 2x - 3. However, its differential du = 2 dx doesn't provide much encouragement, since we have to account for (3x + 4) dx.

However, we can solve u = 2x - 3 for x and substitute the result for x in the integral, then hope that what we end up with will be integrable.
We see that x = (u + 3) / 2, while dx = 1/2 du.
We can therefore replace dx with 1/2 du and (3x + 4) with 3 (u+3) / 2 + 4 to obtain the indicated integral, which we then simplify into a sum of power functions.
The resulting integral is easily evaluated by the usual methods..

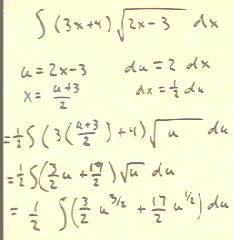
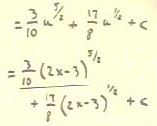
If we wish to integrate sin^5(`theta), as indicated below, we are at first inclined to use the substitution u = sin(`theta), using the 'inner function' of the composite function. However, in this case we would obtain du = cos(`theta) d`theta, and we do not have a cosine factor available.

Instead we use the fact that sin^2(`theta) = 1 - cos^2(`theta) as follows:
We first write sin^5(`theta) as sin(`theta) * ( sin^2(`theta) ) ^ 2 = sin(`theta) * (1 - cos^2(theta)) ^ 2.
We then use the substitution u = cos(`theta), so that du = - sin(`theta) d`theta.
The integral then transforms, and is simplified, as in the fourth line below.
We easily use the power function rule to obtain the result in the fifth line, after which we will proceed in the usual fashion.

This strategy will work with any odd power of a sine or cosine function.

Integration by Parts

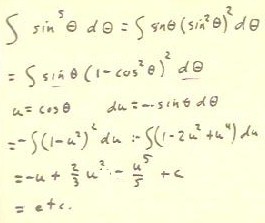
If we apply the product rule to the product (u v), where u and v are two functions of the same single variable and the derivative is with respect to this variable, we obtain the equation in the first line below. We will rearrange this equation to obtain an expression for the integral of v' u:

We first rearrange the equation as in the second line (think of reversing the sides, reversing u'v and v'u to v u' and u v' so the derivatives are on the end, and subtracting v u' from both sides).

We integrate each term of the resulting equation.

Noting that an antiderivative of (uv)' is just uv, we obtain the form in the last line of the figure.

At this point we don't worry about the integration constant, because there are still integrals to be evaluated and they will produce constants.

The form in the last line is the formula for integration by parts, which will be illustrated with subseqjent examples.

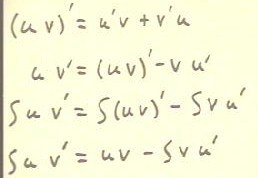
We apply the formula to the integral of x sin(x).

It is a good idea to first write down the formula for integration by parts above the integral to be performed.
If we let u = x and v' = sin(x), then our integrand has the form u v', and we will be able to apply the formula for integration by parts.
This of course does not guarantee that we will get a useful result from the formula, though in this case we well.
Since the application of the formula requires us to know u' and v, we find the derivative of u and and antiderivative of v, as indicated in the fourth line below.
We then substitute into the right-hand side of the formula, obtaining the result in the fifth line which is slightly simplified in the sixth.
We easily evaluate the required integral and obtain the solution in the last line.
You should verify that the derivative of this function is x sin(x).

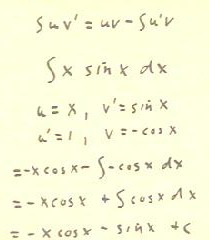
A slightly more complicated example is shown below, in which we attempt to integrate x^2 e^x..

Below the integral we list four different ways in which we could express the integrand as u v'.

You should verify that in each case u v' = x^2 e^x.

The first two ways of breaking down the integrand yield simple expressions for v leading to integrals of v u' which we easily evaluate.

We note that the first way gives us an integral involving a higher power of x then that with which we started, while the second gives us in integral involving a lower power of x.

The third way of breaking down the integrand gives us a function v' which we cannot easily integrate, so we reject this choice.

The fourth way of breaking down the integral yields a fairly complicated expression for u', leading us to avoid this choice at least for the time being. If nothing else works we might return to it.

This leaves us with the first two ways of breaking down the integral. Of these we choose the second, because it reduces the power of x in the required integral. This seems like a better strategy for simplification than increasing powers of x (there is no end to increasing powers but there is an end to decreasing powers).
Using the u and v' of the second breakdown, we see that the right-hand side of the formula for integration by parts will give us the expression in the sixth line below.

The integral in the resulting expression, as we have seen, involves a lower power of x than that in the original. However, we still cannot evaluate this integral any straightforward substitution.

We therefore apply integration by parts to this new integral, using u = 2x in order to again reduce the power of x
The expression u' v to be integrated here is just 2 e^x, which we can integrate easily.
We see in the seventh line the expression to which our original integral reduces, where u and v refer to the breakdown of the second application of integration by parts.
Substituting the expressions for the new u' and v, we obtain the expression the last line, which will be easily evaluated and simplified.

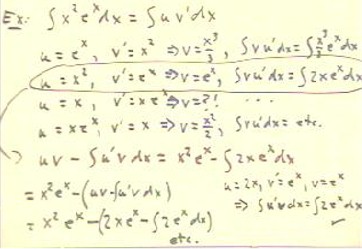
We can apply integration by parts the integral of ln(x), as in the example below.

At first it seems difficult to find a u and a v, since there is only one function, ln(x), involved.
We can, however, express ln(x) as 1 * ln(x).
Using this trick, we could either let u = 1 and v' = ln(x) (a bad idea, since then we would have to integrate v' = ln(x), and that is the problem we're trying to solve), or u = ln(x) and v' = 1 (we obviously will choose this breakdown).
The rest of the process is very straightforward, as indicated below. The trick was to find the functions u and v'.

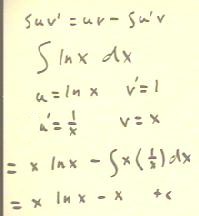
We can also apply integration by parts to find the integral of cos^2(`theta):

We think of cos^2(`theta) as cos(`theta) * cos(`theta) and let u = cos(`theta), v' = cos(`theta).
The rest of the process seems straightforward, as illustrated below.
However, by the last line we begin to suspect that we are running in circles, because we are back to in integral of cos^2(`theta).

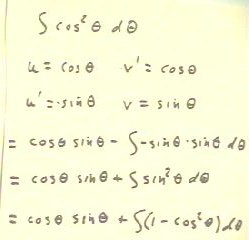
However, if we persist we see that the integral of the squared cosine has difference signs on both sides. This suggests to we might add this term to both sides to obtain the equation in the third line below.

Now, as if by magic, we see that we can simply divide both sides by 2 at obtain an expression for the integral of the squared cosine.

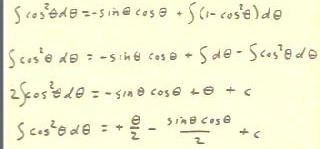
To integrate the expression below, we might wish to let u = 1 - x^4.

However, we would then require an x^3 to give us a du. Solving for x to obtain x = (1 - u) ^ (1/4) might be considered, but in this case it won't help.

Since we have x dx waiting to be used, we might try the substitution u = x^2 so that du = 2x dx.

This gives us the integral in the third line below.

At this point, if we remember the expressions for the derivatives of the inverse trigonometric functions, it will become very clear what the antiderivative will be.

If you don't remember, look up the derivatives of the inverse trigonometric functions. One of them will jump off the page at you.