Precalculus I Class 02/18

We began by observing two spherical containers full of water.  After holding and comparing their 'feel' everyone was asked the following question:

• If you were dying of thirst and someone offered to trade you a bunch of the smaller containers for six of the larger, what is the smallest number of smaller containers you would accept? 

Answers varied from 18 to 24, which as we will see turns out to be pretty good.

The other question was

• How many times the diameter of the smaller is the larger?

Most people said about twice the diameter, and very few were able to make a decision between more than twice and less than twice the diameter.

So the consensus was that the big sphere contains between 3 and 4 times as much water and is close to twice the diameter of the smaller.

Is this consistent?

No.  As we've seen already if one solid has twice the linear dimension of another geometrically similar solid it has 2*2*2 = 2^3 = 8 times the volume.  We're all very sure that if we were dying of thirst we wouldn't need 48 of the smaller sphere to make up for 6 of the larger.

What is our conclusion about how many times the diameter of the small we have in the large sphere?

If we have less than 8 times the volume, which seems very clear after handling and thinkin' about drinkin' the things, then we conclude that the big sphere is less than twice the diameter of the small.

Measurement shows that the smaller contains 100 ml of water while the larger contains 263 ml of water.

So how many times the diameter of the smaller is the larger?

If y is the volume and x the diameter we expect that the proportionality will be y = k x^3.

We know that the ratio of the volumes y is 

• y2 / y1 = 263 / 100 = 2.63.

So what is the ratio of diameters x2 / x1?

We know that y2 / y1 = 2.63 and y = k x^3 for some constant number k.

This means that y2 = k x2^3 and y1 = k x1^3, whatever diameters x1 and x2 go with volumes y1 and y2.

If this is the case then we can write y2 / y1 as 

• y2 / y1 = (k x2^3) / ( k x1^3).

If we simplify the right-hand side we obtain the following:

• (k x2^3) / ( k x1^3); isolating k / k, which is 1, and using the identity property of multiplication we get
• x2^3 / x1^3; since (a/b)^n = a^n / b^n we can write this as
• (x2/x1)^3.

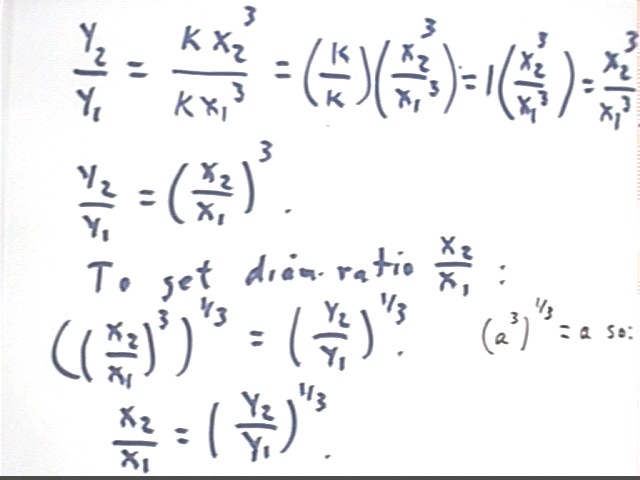
Thus we see that

• y2 / y1 = (x2 / x1)^3

To get x2 / x1 we take the 1/3 power of both sides, obtaining

• ((x2 / x1)^3)^(1/3) = (y2/y1)^(1/3) so by laws of exponents
• x2 / x1 = (y2 / y1)^(1/3).

What then should be the ratio of diameters for our spheres?

Recall that the ratio of volumes is y2 / y1 = 2.63.  So the ratio of diameters will be

x2/x1 = (y2/y1)^(1/3) = 2.63 ^ (1/3) = 1.38.

How can we check this out?

We could measure diameters, but it's hard to line up the diameter with the meter stick.  So we wrap a thin wire around the widest part of each sphere and find that the circumferences are 29 cm and 35 cm.  This doesn't give us the 1.38 ratio we expect.

Directly measuring diameters with calipers we get 5.87 cm and 8.00 cm, for a ratio of x2/x1 = 8.00 / 5.87 = 1.36, pretty close to 1.38.

We don't expect this to be completely accurate because we're measuring the outer, not the inner diameter.  Inner diameters will be a bit less than the diameters measured.

Challenge:  Can you find the thickness of the glass from this information?

Next we observed the time required for a chain to oscillate back and forth 10 times in 'jumprope' fashion, as a function of the tension at the end of the chain.  We obtained the following:

We wish to test whether any of the common power-function proportionalities a = x^2, a = x^.5, a = x^-.5, a = x^-1, a = x^-2 will work for this data.

We test y = a x^2 and 6 = a / x^2  in the figure below.

For each function we determine the value of a for each data point.  If a turns out to be constant or nearly so we figure that we have a good model.

• For y = a x^2 we have a = y / x^2, giving us the indicated results.  a is nowhere near constant so we reject this model.
• For y = a x^-2 = a / x^2 we have a = y * x^2, giving us the indicated results.  Again a is nowhere near constant so we reject this model. 

 Testing the model y = a / x^.5, for which a = y * x^.5, we do obtain reasonably consistent values for a:

Averaging our values of a to get about a = 70, we conclude that y = 70 x^.5 is a good model.