Precalculus I Class 02/20

Quickly plot:

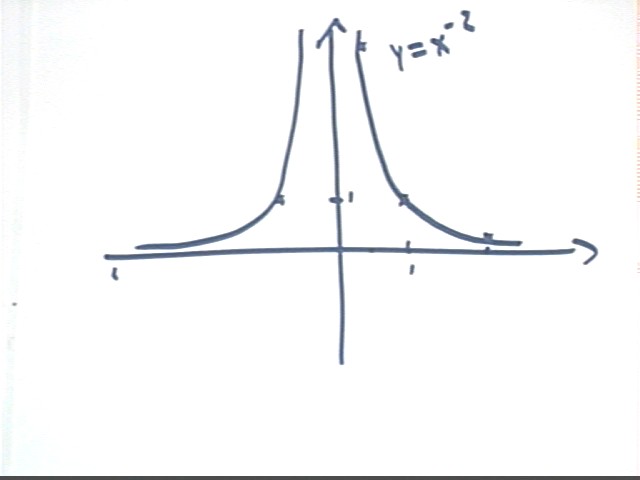
y = x^-2

We mentally calculate y at x = 1/2, 1 and 2, obtaining values 4, 1 and 1/4.  Plotting these basic points and recalling how the vertical and horizontal asymptotes are formed we get the first-quadrant part of the graph as shown below.

We then note that negative values of x will give the same results as the corresponding positive values, making the graph symmetric with respect to the y axis.  This allows us to sketch the second-quadrant part of the graph as a 'reflection' of the first-quadrant part.

y = x^3

We mentally calculate y at x = 1/2, 1 and 2, obtaining values 1/8, 1 and 8.  Plotting these basic points and recalling how the vertical and horizontal asymptotes are formed we get the first-quadrant part of the graph as shown below.

We then note that negative values of x will give the same results. except negative, as the corresponding positive values, making the graph symmetric with respect to the y axis.  This allows us to sketch the second-quadrant part of the graph as a 'reflection' of the first-quadrant part.

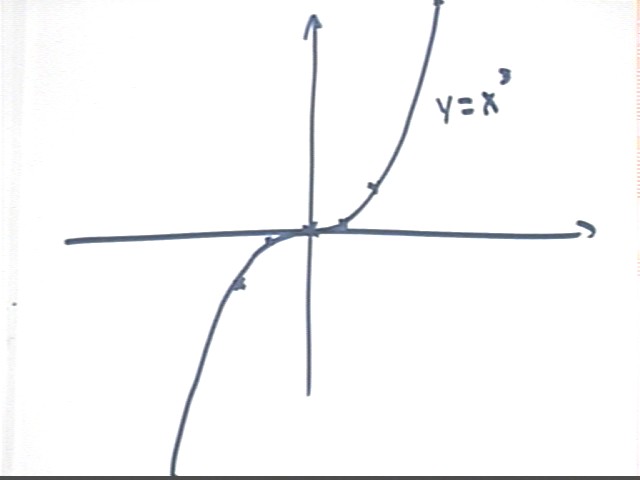
y = x^4

We mentally calculate y at x = 1/2, 1 and 2, obtaining values 1/16, 1 and 16.  Plotting these basic points and recalling how the vertical and horizontal asymptotes are formed we get the first-quadrant part of the graph as shown below.  We note that compared to a parabola the values of y = x^4 stay closer to the x axis when x < 0, especially when x is near 0, and that the graph goes up much more quickly when x > 1.

We then note that negative values of x will give the same results as the corresponding positive values, making the graph symmetric with respect to the y axis.  This allows us to sketch the second-quadrant part of the graph as a 'reflection' of the first-quadrant part.

Note that steps in the construction of the graph of y = .1 (x+3)^4 - 1, a problem given below, are also indicated on this graph.  The explanation will be given with that problem.

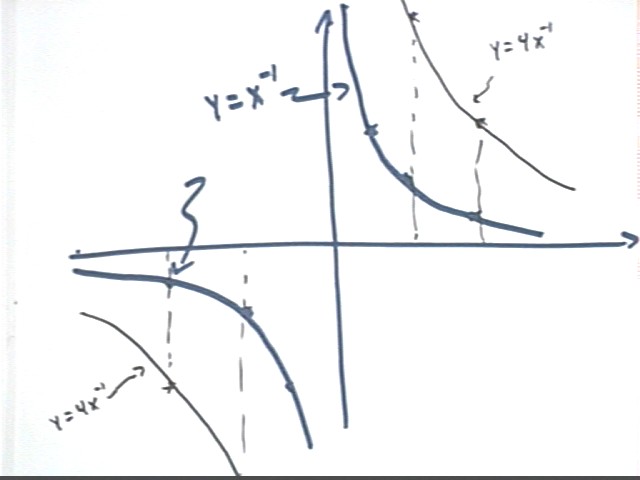
y = x^-1

We mentally calculate y at x = 1/2, 1 and 2, obtaining values 2, 1 and 1/2.  Plotting these basic points and recalling how the vertical and horizontal asymptotes are formed we get the first-quadrant part of the graph as shown below.

We then note that negative values of x will give the same results as the corresponding positive values, making the graph symmetric with respect to the y axis.  This allows us to sketch the second-quadrant part of the graph as a 'reflection' of the first-quadrant part.

Note that steps in the construction of the graph of y = 4 x^-1, part of a problem given below, are also indicated on this graph.  The explanation will be given with that problem.

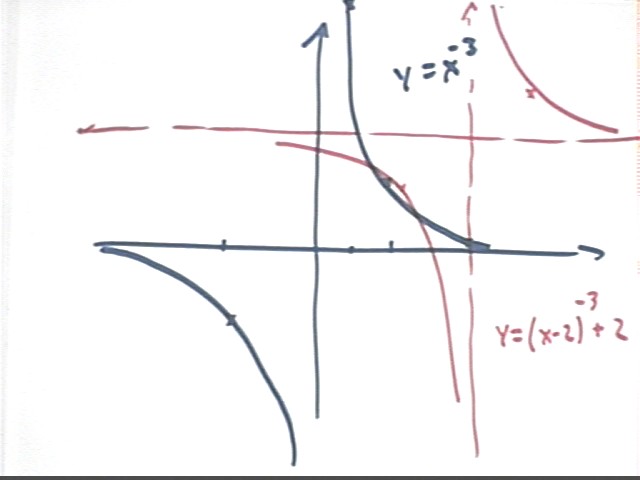
y = (x-2)^-3 + 2

We construct the y = x^-3 graph as a basis for the desired graph.

The graph of y = (x-2)^-3 + 2 is shifted 2 units to the right and 2 units up.  The easiest way to construct the resulting graph is to sketch x and y axes both shifted 2 units in the positive direction, then to shift the graph of y = x^-3 so that the resulting graph will have asymptotes at the 'new' set of axes. 

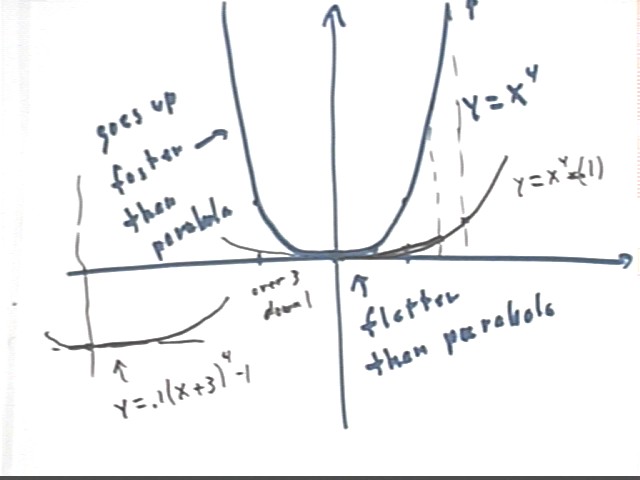
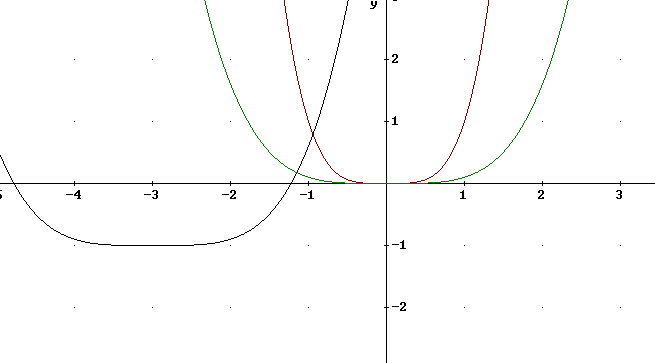
y = .1 (x+3)^4 - 1

Refer to the graph of y = x^4, sketched above.  

We first vertically stretch that graph by factor .1, which moves each point 10 times closer to the x axis to give us the graph of 6 = .1 x^4.

We then shift the new graph -3 units in the horizontal direction and -1 units in the vertical direction.  This moves its 'vertex' from (0, 0) to (-3, -1), where we sketch a 'new' set of axes to assist in sketching the translated graph.

These graphs are shown more accurately in the figure below:

y = 4 * x^-1 + 3

Refer to the graph of y = x^-1, sketched above.  

We first vertically stretch that graph by factor 4, which moves each point 4 times further from the x axis to give us the graph of y = 4 x^-1.

We will then shift the new graph 3 units in the vertical direction.  This moves its 'vertex' from (0, 0) to (0, 3), where we will sketch a 'new' set of axes to assist in sketching the translated graph.  This is not shown on the graph above.

The corresponding graphs are all shown accurately in the figure below:

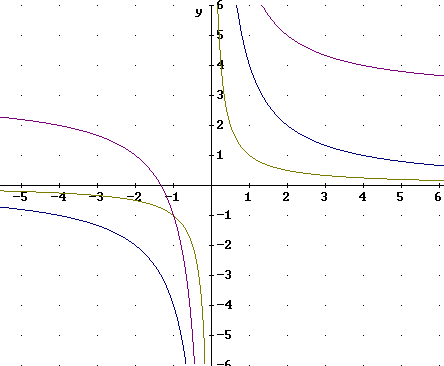
Suppose that a(n) = a(n-1) + 3, a(1) = 9.

Find a(2), a(3), a(4), a(5) and a(3598).

To get a(2):  Plug in 2 for n to get

• a(2) = a(2-1) + 3

Simplify to get

• a(2) = a(1) + 3

Substitute the known value of a(1) to get

• a(2) = 9 + 3

Simplify to get 

• a(2) = 12.

To get a(3):  Start with a(n) = a(n-1) + 3 and plug in 3 for n to get

• a(3) = a(3-1) + 3

Simplify to get

• a(3) = a(2) + 3

Substitute the known value of a(2) to get

• a(3) = 12 + 3

Simplify to get 

• a(3) = 15.

To get a(4):  Start with a(n) = a(n-1) + 3 and plug in 4 for n to get

• a(4) = a(4-1) + 3

Simplify to get

• a(4) = a(3) + 3

Substitute the known value of a(3) to get

• a(4) = 15 + 3

Simplify to get 

• a(4) = 18.

At this point we see that a(n) will go up by 3 every time n goes up by 1, so we have the sequence

a(1), a(2), a(3), a(4), a(5), ... =

9, 12, 15, 18, 21, ... 

So what is that term a(3598)?

Starting at a(1) we have to make 3598 - 1 = 3597 'jumps' each of 3 units.

The total 'jump' is therefore 3 * 3597 = 10791.

You started at 9 so you end up at 9 + 10791 = 10800.

So a(3598) = 10800.

Now try the relation a(n) = a(n-1) + 3 n, a(1) = 9.  Get the first few numbers, then try to predict a(3597).

We get sequence a(1), a(2), a(3), a(4), a(5), ... equal to

9    15    24    36   51  ...

The details are shown below, where we have used subscripts (e.g., a with subscript n) instead of function notation a(n):

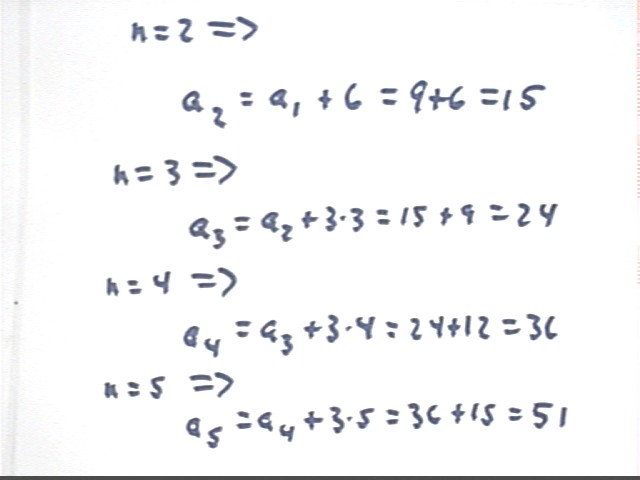
Analysis of differences tell us that this sequence is quadratic.

• As you've seen in homework exercises the slopes of a graph of a quadratic function, for equal intervals, change by the same amount with each new interval.
• If the values of the sequence a(n) were plotted vs. n and slopes calculated at intervals of 1 unit, the slopes would be equal to the differences 6, 9, 12, 15, ...
• It follows that a(n) is a quadratic function of n.
• Note that the differences of the 'linear' sequence are constant.  So the 'second difference' of the quadratic sequence is constant, giving us the progression from quadratic to linear to constant.  This will be a characteristic of any quadratic function evaluated at equal intervals.

So a(n) is a quadratic function of n.  It follows that a(n) is of form y = a n^2 + b n + c, the the a in 'a(n)' refers to the function a and the a in front of n^2 refers to the constant a in the form of a quadratic function.

We can substitute any three 'data points' to get a, b and c.

Using the first three (n, a(n)) points (1,9), (2,15) and (3,24) we get equations:

• a(1^2) + b(1) + c = 9
• a(2^2) + b(2) + c = 15
• a(3^2) + b(3) + c = 24

These equations can be solved using the techniques developed in the first few classes.  Solutions are a = 1.5, b = 1.5 and c = 6.

So a(n) = 1.5 n^2 + 1.5 n + 6.

We got the function so how do we find a(3597)?

Plug in n = 3597.  We get

a(3597) = 19,413,015

There's another way to get this result, using simple arithmetic and common sense.  See if you can figure it out.

Note that x^5/8 = 12 means (x^5) / 8 = 12, since exponentiation precedes division.

If we wanted the exponent to be 5/8 we would have to write this x^(5/8) = 12.

We solve this equation as indicated in the figure below.