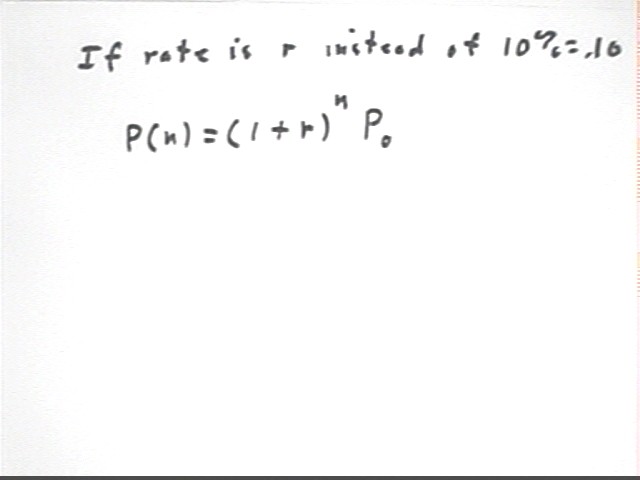
Precalculus I Class 02/25

More Notes on Transformations

We look at how the basic points allow us to graph parabolas.  We will start with the graph of y = x^2 and see how that basic points change as we transform this graph into that of y = 1/4 ( x - 3)^2 - 2.

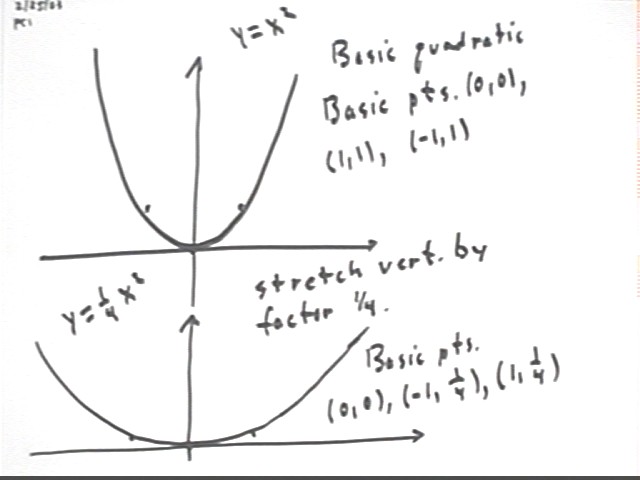
The figure below shows the graph of the basic quadratic function y = x^2.  This graph has the three basic points (-1, 1), (0, 0) and (1, 1).

The figure also shows the result of stretching the graph in the vertical direction by factor 1/4, which results in the basic points (1, 1/4), (0, 0) and (1, 1/4), each point being 1/4 the distance of the original basic points from the x axis.

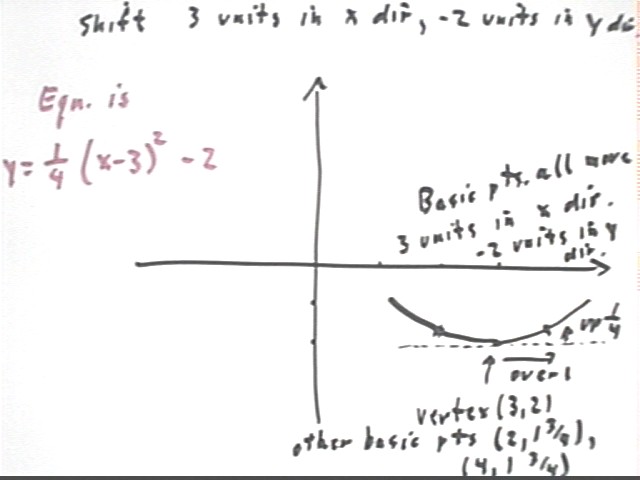
We now shift the vertically stretched graph 3 units in the x direction and -2 units in the y direction, to obtain the graph of y = 1/4 ( x - 3)^2  - 2.

• The basic points each move 3 units in the x direction and -2 units in the y direction.

The point (-1, 1/4) moves to (-1 + 3, 1/4 - 2) = (2, -1 3/4).

The point (-0, 0) moves to (0 + 3, 0 - 2) = (3, -2).

The point (1, 1/4) moves to (1 + 3, 1/4 - 2) = (4, -1 3/4).

• Using these three points we can make a reasonable sketch of the new parabola.

We can graph any parabola using the idea of the three basic points.  We construct the graph of y = .3 x^2 - 6 x + 40.

We first note that this graph can be constructed by a vertical stretch followed by horiz and vertical shifts, and that the vertical stretch must be by factor .3.  To see why see how that the vertical stretch factor 1/4 used in the preceding construction remains as the coefficient of x^2.  The only way x^2 can have coefficient .3 is for the initial vertical stretch factor to be .3.

• We first find the vertex at x = - b / (2a) = 10.  Plugging x = 10 back into the formula we get y = 10.
• So the vertex lies at (10, 10).  So this graph was constructed by first vertically stretching the basic y = x^2 graph by factor .3, then shifting it 10 units in the horizontal direction and 10 units in the vertical direction.
• Since this function involves vertical stretch factor .3 we understand that the 3 basic points of the graph must be the vertex and points lying 1 unit right and left of the vertex and .3 units higher.
• This results in basic points (9, 10.3), (10, 10) and (11, 10.3), inciated in the figure below and in the following figure. 

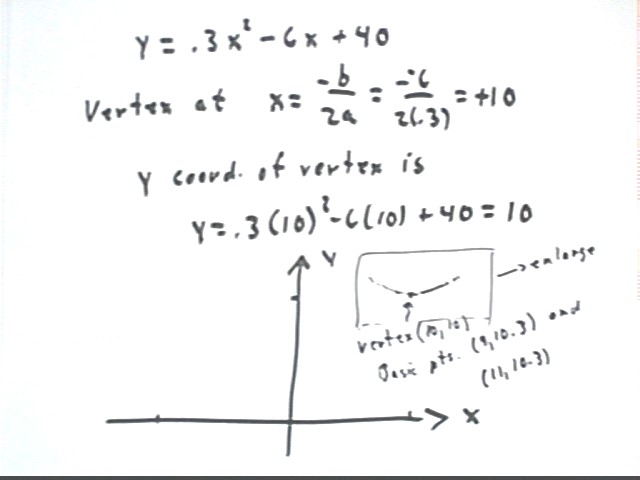
This figure enlarges the rectangular region indicated in the preceding figure.  We see how the vertex at (10, 10) is 'flanked' by the basic points (11, 10.3), lying 1 unit to the right and .3 units higher than the vertex, and (9, 10.3), lying 1 unit to the left of the vertex and .3 units higher.

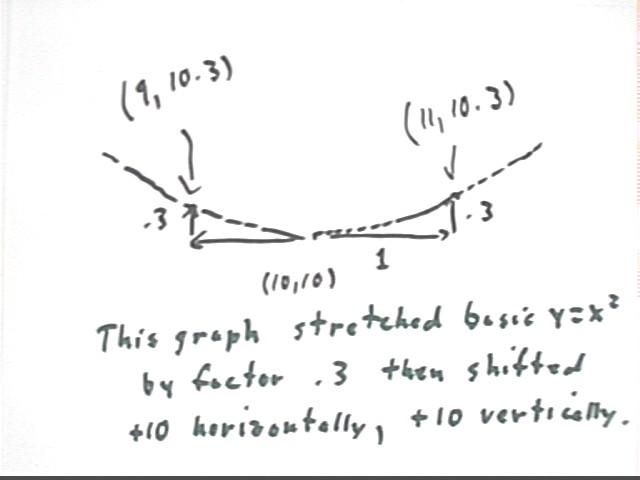
The transformation process is summarized below.  We can see that this process results in the function y = .3 (x - 10)^2 + 10.

The original function was y = .3 x^2 - 6 x + 40.  Is this the same as the function y = .3 (x - 10)^2 + 10?

We see by that the two functions are the same by expanding y = .3 ( x - 10)^2 + 10, as shown below.

Solve z^5/8=12

First write the thing out.

This means (z^5) / 8 = 12, not z^(5/8) = 12.  This is because exponentiation ^ precedes multiplication or division.

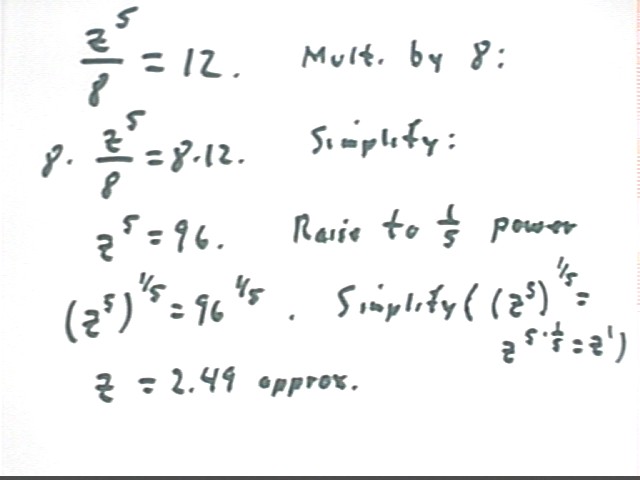
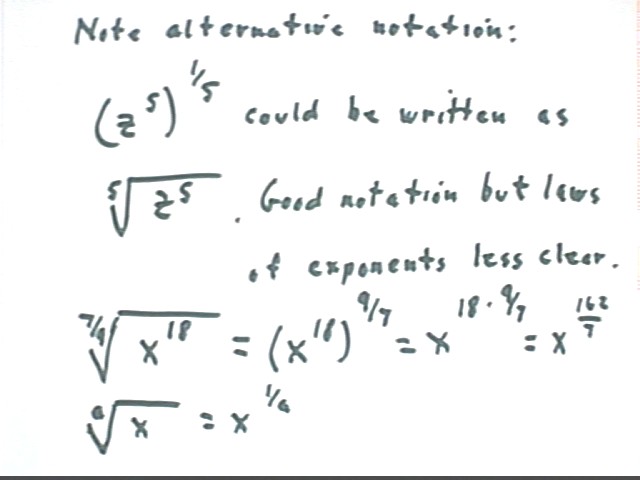
Solve 12 y^(3/7) = 9.

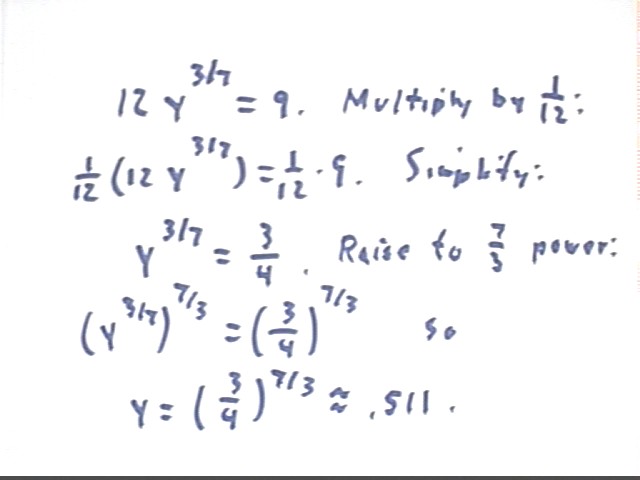
Evaluate y = .4 x^2 - 16 x + 5 at x = 0, 5, 10 and 15 to form a sequence.  Find the ave rate of change of this function for each interval.  Then find the first and second differences of this sequence.

We can evaluate, obtaining y = 5, -65, -115 and -145 at x = 0, 5, 10, 15.

Using the DERIVE command vector(.4 x^2 - 16 x + 5, x, 0, 15, 5) we approximate to get [5, -65, -115, -145], meaning that the sequence of values is 5, -65, -115, -145.

Average rates of change are:

• For first interval change in y is -65 - 5 = -70 and change in x is 5 - 0 = 5, so ave rate of change is -70 / 5 = -14.
• For second interval change in y is -115 - (-65) = -50 and change in x is 10 - 5 = 5, so ave rate of change is -50 / 5 = -10.
• For the third interval you will find that the ave rate of change is -6.
• Note the pattern.  Each rate is 4 greater than the preceding.  So the next several rates, corresponding to the next several 5-unit intervals, are -2, 2, 6, 10, 14, 18, 22, ... 

Finding first and second differences of the sequence 5, -65, -115, -145 we obtain

• First difference is -70, -50, -30
• Second difference is 20, 20.

If the pattern continues then the second differences will continue to be 20, from which we can construct additional first differences and from them additional members of the sequence.

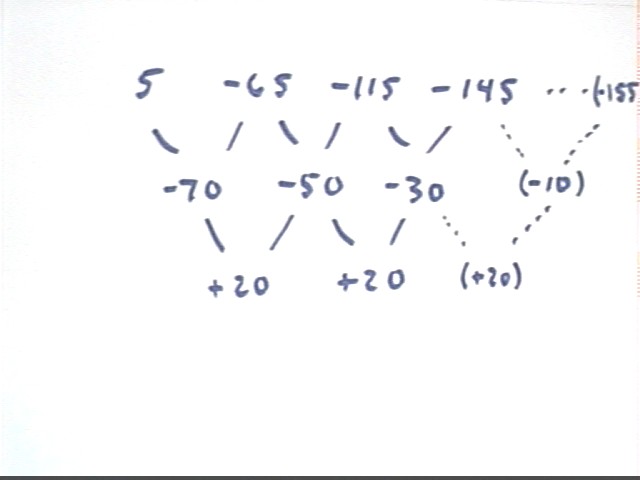
If you are given $1000 at 10% interest compounded annually you can easily calculate the principle in successive years, as shown below.

To figure out the principle after 100 years, we hope there's a shorcut.

As shown below, adding 10% every year is the same as multiplying by 1.10 for each year.   Thus for example after 3 years the principle will be 1.10^3 times the initial principle.

If we let P0 stand for the initial principle then to get the principle after n years we simply multiply P0 by 1.10^n.

The function P(n) = 1.10^n * P0 is an exponential function, so called because the variable n appears as the exponent.

If instead of 10% = .10 the rate was r then the 'base' 1.10 would become 1 + r and the function would be P(n) = (1 + r)^n * P0.