Precalculus I Class 03/04

More Notes on Transformations

From the Homework "Final Assignment prior to Test #1 page 2 of 2, problem 2.

If a(n+1)=a(n)+0.5n, with a(0)=2 then what are the next 4 elements of the sequence?  What is the 100th element of the sequence?

Let n = 0:

• a(0+1) = a(0) + 0.5 * 0
• a(1) = a(0) + 0.  We know that a(0) = 2 so
• a(1) = 2 + 0 = 2.

Let n =1:

• a(1+1) = a(1) + 0.5 * 1
• a(2) = a(1) + 0.5.  We just found that a(1) = 2 so
• a(2) = 2 + 0.5 = 2.5.

Let n = 2:

• we get
• a(3) = a(2) + 0.5 * 2.  Since a(2) = 2.5 we get
• a(3) = 2.5 + 2 = 3.5.

The figure below summarizes the first few steps of this process.  The arrows indicate how at each step we substitute the value obtained in the preceding step. 

We therefore have the following points of form (n, a(n)):

• (0,2), (1, 2), (2, 2.5), (3, 3.5).

The y values are 2, 2, 2.5, 3.5. 

• The differences in y values are 0, .5, 1.
• These differences seem to be increasing by .5 each time.  This indicates that a quadratic model might be appropriate.

We can create a quadratic model using any three data points (get 3 simultaneous equations, solve, get the y = a n^2 + b n + c form).  The resulting model can be evaluated at n = 100.

• a(n+1)=a(n)+0.5n.  The term +0.5 n  is linear in n, so we expect that a(n) will be a quadratic function of n.

If f(x) = ax^2 +b x + c, then what symbolic expression stands for the average slope between x=h and x=k

The average rate of change is change in f(x) / change in x.

Between points x = h and x = k the change in f(x) is f(k) - f(h), and the change in x is k - h. 

Therefore the average rate of change is (f(k) - f(h) ) / (k - h).

Substituting into f(x) = a x^2 + b x + c we get f(k) = a k^2 + b k + c and f(h) = a h^2 + b h + c so that

• (f(k) - f(h) ) / (k - h) =

  ( a k^2 + b k + c - ( a h^2 + b h + c) ) / ( k - h ) =

  ( a k^2 + b k + c - a h^2 - b h - c) / (k - h) =

  ( a(k^2-h^2) + b ( k - h) ) / ( k - h) =

  ( a ( k - h ) ( k + h ) + b ( k - h) ) / ( k - h) =

  a(k+h) + b.

The process is summarized in the solution below, which includes reference both to the rate of change idea and the slope idea:

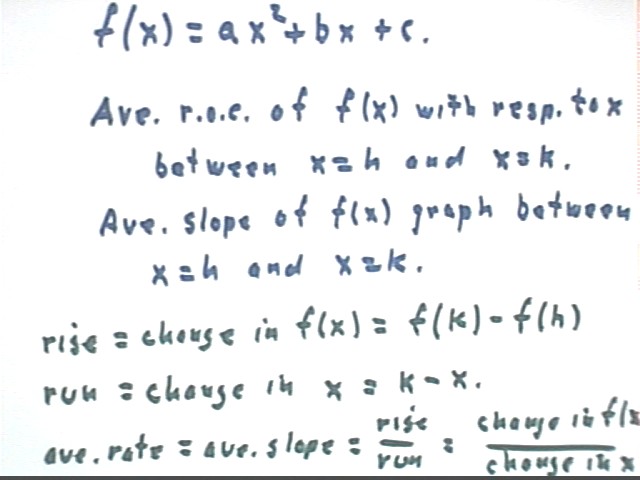
From the "Introduction to Exponential Functions", page 5 of 19.

Regarding doubling in problem 5, 6 and 7.

We want to solve the equation 2P0 = P(t)

P(t) = P0(1 + r)^t

The doubling equation 2 P0 = P(t) becomes

• 2P0 = P0(1 + r)^t

If we divide both sides by P0 we get

• 2 = (1 + r)^t

How do we solve for t in the equation 2 = (1 + r)^t?

To solve the equation for t you need to use logarithms, which we haven't done yet (soon, within a couple of weeks).

The only alternative is to solve by trial and error.  To do this you need a numerical value for r.

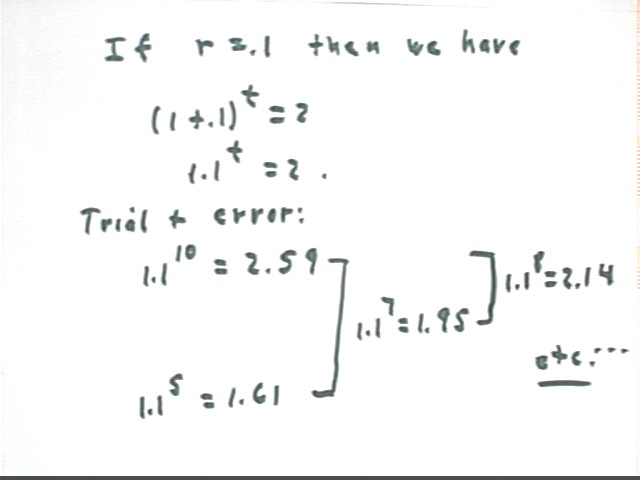
For example if r = .1 we have

2 = (1 + .1) ^ t or

2 = 1.1^t.

We first find a value for t that makes the result bigger than 2.  t = 10 is a good choice, giving us

• 1.1^10 = 2.593

Now we find a value that makes the result smaller than 2:

• 1.1^5 = 1.61.

Now we've got the number 2 'bracketed' between 1.1^5 = 1.61 and 1.1^10 = 2.59.

We now pick an exponent between 5 and 10.  To keep it simple we'll use either 7 or 8.  The class has chosen 7.  We find that

• 1.1^7 = 1.95.

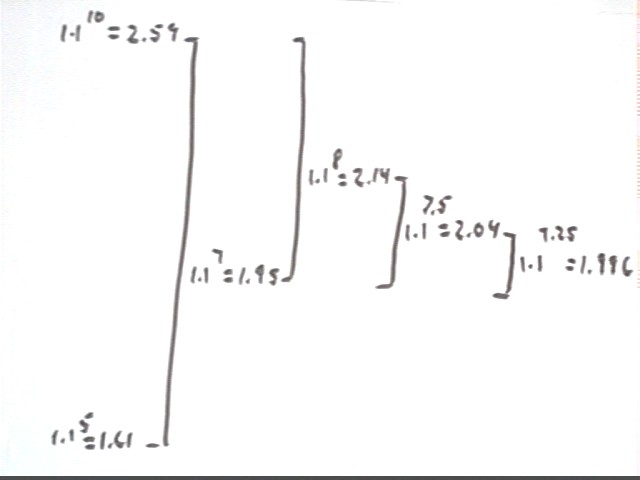
We have narrowed our bracket to the interval [7, 10].  We choose a number in this interval.  A quick look at the numbers tells us that 8 is a good choice.

• 1.1^8 = 2.14.

Now our bracket is [7, 8].  Taking the midpoint of our bracket we evaluate the number at 7.5:

• 1.1^7.5 = 2.04.

Now our bracket is [7, 7.5].  Taking the midpoint of our bracket we evaluate the number at 7.25:

• 1.1^7.25 = 1.996.

Now our bracket is [7.25, 7.5]. 

We could continue to refine our brackets but we're confident that the result to 2 significant figures is 7.3.

We can make this process as accurate as we like.

The bracketing process is illustrated below:

Quick preview of solution to 2 = (1 + r)^t:

Take log of both sides to get

log(2) = log( (1+r) ^ t).  Laws of exponents reversed for logs give us

log(2) = t log(1+r) so that

t = log(2) / log(1+r).

For example if r = .1 we have

t = log(2) / log(1.1) = 7.2725.

Problem:

How do we express y = 6 e^(.07 t) in the form y = A * b^t?

Since e^(.07 t) = (e^.07)^t = 1.07^t, approx. to 3 significant figures.

We have used the law (a^b)^c = a^(bc).

So y = 6 e^(.07 t) can be written as y = 6 * 1.07^t.

The expression

• y = 6 * 1.07^t

is in the form y = A * b^t with A = 6, b = 1.07.

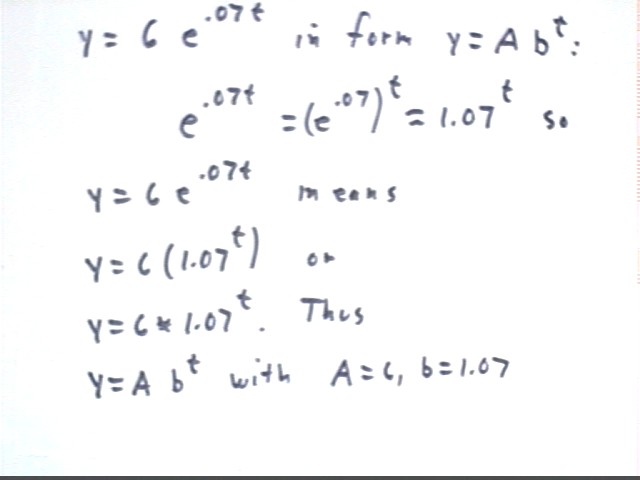
Which of the power functions y = a x^.5, y = a x^-.5, y = a x^2 and y = a x^-2 best fits the following data:  When x takes values 27.666, 7.027, 3.034 and 1.749, respectively, y takes values 6, 12, 18 and 24. 

Since x values decrease as y values increase we suspect that it's one of the negative powers.

If it's y = a x^-.5 then we can solve for a if we multiply both sides by x^.5:

y = a x^-.5  Multiply by x^.5:

x^.5 * y = a x^-.5 * x^.5.  Simplify right-hand side:

x^.5 * y = a x^(-.5 + .5) or

x^.5 * y = a x^0 or since x^0 = 1

x^.5 * y = a.

Since a is to be constant, a = y * x^.5 should always be about the same.  So we evaluate a = y * x^.5 at the given points to see whether a comes out nearly constant:

We see that a = x^.5 * y is very nearly constant so we conclude that y = a x^-.5, or in this case more specifically y = 31.5 x^-.5 is a good model.

The figure below shows how a table of y vs. x leads to a graph of y vs. x.  The fact that the graph is decreasing, with possible asymptotes at the x and y axes, shows us that one of the functions y = a x^-2 or y = a x^-.5 will be the appropriate choice (note that the other two functions, with positive exponents, would be increasing functions and not appropriate to our data).

We could start with either y = a x^-2 or y = a x^-.5.  We choose y = a x^-.5 and we get lucky on our first try.