Suppose that we have the following data for depth vs. time:

When his water flowing at the greatest rate?

You probably answered that the water was flowing at the greatest rate at the beginning, and you probably noticed that the rate of flow continues to decrease with every new data point. You can tell this because the depth numbers tend to have to greatest change for the earliest times and the least change for the later times.

Of course the question asked was about the rate at which the water is flowing, not about the rate at which the depth changes. However it is probably obvious to you that what causes the depth change is the flow of water and that the rates are inextricably linked, with one rate being high when the other is high and one low when the other is low. So we can answer the question of when the flow rate was the greatest by determining when the rate of depth change is the greatest.

According to the data, does the rate at which water flows decrease with every new data point?

If we just look at the changes in the depth, we see that depth falls by 20 cm, then by 18 cm, then by 7 cm, then by 5 cm, then by 13 cm, then by 12 cm, 10 cm, 5 cm, 4 cm, and 3 cm. Except for the 7 cm and the 5 cm drops between the 18 and 13 cm drops, the numbers do indeed seem to be decreasing. Why should there be an abrupt difference in the pattern for these two numbers?

The answer to this dilemma has to do with the time intervals corresponding to each drop. The 7 and 5 cm drops occur over five-second intervals, while all other drops occur over ten-second intervals. So naturally the drops will be smaller over the five-second intervals. Clearly any rate that we infer from the data will have to involve both the change in altitude and the time of which the change takes place.

Most people would agree that the number of cm change in depth per second would be a good indication of the rate which the depth is changing. During the first 10 seconds the depth changes by -20 cm, which is an average rate of change of -2 cm for each second (we say average rate because the rate is changing from instant to instant; any calculation done over a time interval, as over this 10 second interval, gives us in average of all the different rates over that interval). Note that, since the depth is decreasing, the every rate of change turns out to be negative. What are the average rates for each of the other time intervals?

You probably obtained your average rates by taking the drop in cm and dividing by the number of seconds. This is the common sense approach, and it is correct. We summarize by stating that

Average rate of depth change = depth change / time required for the change.

The average rates are therefore

-20 cm / 10 sec = -2.0 cm/sec

-18 cm / 10 sec = -1.8 cm/sec

-7 cm / 5 sec = -1.4 cm/sec

-5 cm / 5 sec = -1.0 cm/sec

-13 cm / 10 sec = -1.3 cm/sec

-12 cm / 10 sec = -1.2 cm/sec

-10 cm / 10 sec = -1.0 cm/sec

-5 cm / 10 sec = -.5 cm/sec

-4 cm / 10 sec = -.4 cm/sec

-3 cm / 10 sec = -.3 cm/sec.

We see that the average rates are indeed decreasing, except for a glitch on the fourth rate (the -1.0 doesn't quite fit the pattern). Whether this is a minor glitch or a major problem with our data is an important question, but not for our present purposes, so we leave this question for later.

We can use the function to create a data table for any given set of times t. For example let us use times separated by intervals of 20 seconds, starting at 0. We obtain the data points

( 0,depth(0) )   =   (0, 100)

(20,depth(20) ) =   (20, 64)

(40,depth(40) ) =    (40, 36)

(60,depth(60) ) =     (60, 16)

(80,depth(80) ) =      (80, 4)

(100,depth(100) ) = (100, 0)

The first two data points correspond to the time interval of 20 seconds and a depth change of -36 cm, for an average rate of -1.8 cm/sec.

For the next two data points the time interval is 20 seconds and depth change is -28 cm, so the average rate is -1.4 cm/sec.

The remaining rates can be easily found. They are -1.0 cm/sec, -.6 cm/sec and -.2 cm/sec.

We note that there's a pattern to these average rates. During each 20 second time interval the average rate changes by .4 cm/sec. We will see later that this is one of the characteristic properties of a quadratic function: the average rate at which a quadratic function changes, changes at a uniform rate.

We can do the same sort of analysis with any function. However the property of the uniformly changing rate of change from one interval to another is unique to the quadratic functions.

If we graph our original data points, we obtain the following graph:

We see that the tendency of the graph is to decrease faster at the beginning than at the end. The graph is steeper when the flow rate is greater. In some way the steepness of the graph indicates the rate at which depth is changing.

You should be familiar with the idea that the steepness over graph is measured by its slope. You are also probably familiar with the idea that slope is rise/run. We can use these ideas to get a numerical measure of the steepness.

Consider the points on the enlarged graph below. From each point to the next, there is a certain 'run', which is the horizontal displacement from the first point to the second. We see that the horizontal displacements all run in the same direction as the horizontal axis and hence all represent changes in time. The horizontal displacements are all either 10 seconds or 5 seconds (recall that the distance between vertical grid lines was 10 centimeters). These displacements are marked on the graph above the red line segments representing them.

From each point to the next there is also a 'rise', which is a vertical displacement. The vertical displacements run in the same direction as the depth axis and hence measure changes in depth. We note that in this example all depths are decreasing, with a negative vertical displacement from each point to the next. The vertical displacements are -20 cm, -18 cm, -7 cm, -5 cm, etc.. These displacements are clearly marked on the graph as rises.

The red lines marking the runs and the rises form the legs of a series of right triangles. These triangles have been completed with the blue line segments, so each point-to point displacement is represented by a right triangle, with one side parallel to the x axis and the other to the y.

The slope associated with each blue line segment is the rise/run ratio for the corresponding triangle. For example the first triangle has a rise of -20 cm and are run of 10 sec. The slope is therefore rise/run = -20 cm /10 sec = -2 cm/sec. We note that this is identical to the calculation of the average rate over the first interval for our original data.

The remaining slopes shown a the graph, each calculated by a rise/run ratio, are

-18 cm/10 seconds = -1.8 cm/sec.

-7 cm/5 sec. = -1.4 cm/sec.

-5 cm/5 sec. = -1 cm/sec.

-13 cm/10 sec. = -1.3 cm/sec.

These slopes are identical to the average rates calculated previously.

Recall that average rates were calculated by determining depth change per unit of time, so that we divided the depth change by the time required for that depth change. In the case of a slope calculation we divide the rise by the run. Since the rise represents the depth change and the run represents the time required for that change, we see that the two calculations are identical. Thus we see that the slope of a line segment connecting two points on a depth vs. time graph represents the average rate at which depth changes between the two times. 

When we have the graph of a depth vs. time function, we can find the slope between any two points on the graph. As we have seen this slope will represent the average rate of depth change for the corresponding time interval. So if we choose two times, we can find the slope and hence the average rate of depth change for the corresponding time interval. If our depth function is a good model of reality, the average rate we find will be a good approximation of the average rate of the real-world flow. Furthermore if our time interval is short, our average rate will be close to the precise actual rate for any time within the time interval.

The figure below depicts the graph of the function depth(t) = .01 t^2 - 2t + 100 from clock time t = 0 to clock time t = 100 sec.

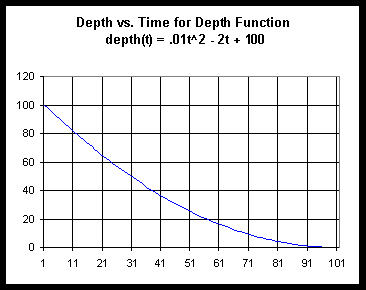
If we wish to determine the average slope predicted by this model between clock times t = 10 sec and t = 30 sec, we can easily do so. The model predicts that at clock time t = 10 sec, the depth will be depth(10) = .01(10^2) - 2(10) + 100 = 81 cm, and similarly that at clock time t = 30 seconds, depth will be depth(30) = 49 cm.

The change in depth will therefore be depth(30) - depth(10) = 49 cm - 81 cm = -32 cm. Since this change takes place over a time interval of duration 20 sec., the average rate of depth change over this interval is -32 cm / 20 sec = -1.6 cm/sec.

This situation is depicted on the graph below:

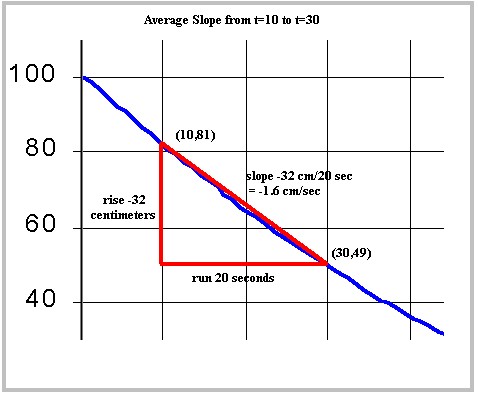
This graph is enlarged version of a portion of the original graph. Recall that the time interval between vertical grid lines is 10 sec. By evaluating the depth function at clock times t = 10 sec and t = 30 sec, we see that the coordinates of the corresponding graph points are (10,81) and (30,49). The red triangle depicts the rise, the run corresponds to the straight line segment between the points. It is clear that the run from the first point to the second corresponds to an elapsed time of 20 sec., and the rise to depth change of -32 cm. The slope rise/run = -32 cm / 20 sec = -1.6 cm/sec therefore corresponds to the average rate at which depth changes during this specific time interval, as predicted by the model.

The figure below depicts another part of the original graph. The red segment has a slope equal to the average rate of depth change between the two corresponding times. The two green segments correspond to two different slopes over the same time interval. The actual slopes of the graph of the function stay much much closer to the slopes of the corresponding green lines than to the slope of the single red line. This figure demonstrates how shortening the time interval dramatically improves the precision of our slope approximations.

One thing about our discussion of when the rate of flow is greater should bother you slightly. We said that the rate of flow was greater when the graph was steeper, which is true. However, for this situation the graph isn't steeper when the slope is greater.

This situation arises because the slopes of the graph are negative. The initial slopes are around -2 cm/sec, while the later slopes have values like -.4 cm/sec. Now it is clear that -.4 use in fact greater than -2 (for example is the temperature was -2 degrees, it would clearly have to rise to reach -.4 degrees). -2 lies further to the left along the number line than -.4. However when we're thinking about how fast the depth of the water changes, we clearly and correctly have the idea that -2 cm/sec is faster than -.4 cm/sec. So where left with a situation in which the slower flow is represented by the greater number. This can be somewhat confusing.

We can result the apparent contradiction between the ideas of faster andgreater if we realize that faster is not a concept for which positive and negative values are appropriate. Speed has no direction and so is never negative (as opposed to velocity, which has a definite direction, and which might be negative). The average speed of the descending water surface starts out around 2 cm per second and decreases to around .4 cm per second, then finally to 0; it is the velocity that goes from -2 cm/second to -.4 cm per second.

The rate of flow out of the container can also be positive or negative. The rate is positive when the water is descending and water is flowing outward from container. The flow rate out of the container is negative when water is rising and water is somehow being drawn into the container.

We use the concept of the absolute value operator to make the mathematical sense of these ideas precise.

We say that the absolute value of any number is its distance from 0 on the number line, independent of whether it lies to the right or to the left of 0. Thus the absolute value of -2 is 2, sense -2 lies 2 units from zero on the number line.

We can also defined absolute value in terms the computer can understand. The computer cannot look at a graph and tell how far the point is from 0. What we do is tell the computer to look and save whether the number has a negative sign in front of it. If it doesn't, the absolute value is just the number. If it does, the absolute value is equal to the negative of the number. For example if the number is 8 it doesn't have negative sign so its absolute value is 8. On the other hand is the number was -6, the absolute value will have equal its negative, which is - (-6) = 6. Either way we end up with a positive number, and that positive number is the distance of the number from the zero point of the number line.

This rule is stated somewhat more formally as follows:

abs(a) = -a if a<0 and abs(a) = a otherwise.

The operator abs is often depicted by putting the number it operates on between two vertical lines. For example, abs(-8) could be depicted by | -8 |. By the time you get to this course you should be familiar with this notation. However if you are not, it isn't a difficult notation understand.

In these terms then, we say that the depth is changing faster when the absolute value of the rate of depth change is greater. We say that the graph is steeper when the absolute value of the slope is greater. In symbols:

speed of depth change = abs(rate of depth change) = | rate of depth change |.

steepness of graph = abs(slope of graph) = | slope of graph |.

1. For the depth vs. time function depth(t) = .02t^2 - 5t + 150, determine the average rate of change of the depth for each of the following time intervals:

t = 0 to t = 20

t = 20 to t = 40

t = 40 to t = 60

t = 60 to t = 80

t = 80 to t = 100

Sketch a graph depicting your calculations.

2. For the time interval from t = 40 sec to t = 60 sec, the 'midpoint time' is t = 50 sec. The term 'midpoint time' is very sensible here; 50 sec is exactly halfway between 40 sec and 60 sec, and is therefore the midpoint of the time interval. Sketch the graph corresponding to each calculation:

Determine the average rate of depth change for the 1-second time interval centered at this midpoint. That is, determine the average rate of depth change between t = 49.5 sec and t = 50.5 sec.

Determine the average rate of change for the six-second time interval centered at the midpoint.

What pattern do you observe?

3. Repeat the preceding two exercises for the temperature function Temperature(t) = 75(2^(-.05t)) + 25. Temperatures are in Celsius degrees and clock time t is in minutes. Instead of depth change rates you will be calculating rates of temperature change. Note that this temperature function is exponential.

4. Repeat the preceding two exercises for the illumination function Illumination(r) = 30 / r^2, where r stands for the distance from the source in meters and illumination is in watts per square meter. Let r range over the following distance intervals:

r = 20 to r = 40

r = 40 to r = 60

r = 60 to r = 80

r = 80 to r = 100.

Instead of rates of depth change with respect to time in cm/sec you will be calculating rates of illumination change with respect to distance, in (watts/square meter) / meter.