Most Basic Properties of Linear, Quadratic, Exponential Functions

You will need to thoroughly understand the graphs of the y = x, y = x^2 and y = 2^x functions.  Much of the Precalculus course is based on these functions.

You should be able to instantly sketch the graph of any of these functions.  Practice until you can do so without reference to these pictures.

Basic Points (defining points) of the Basic Linear Function y = x

Basic Points (defining points) of the Basic Quadratic Function y = x^2

Basic Quantities (defining quantities, two points and asymptote) of the Basic Exponential Function y = 2^x

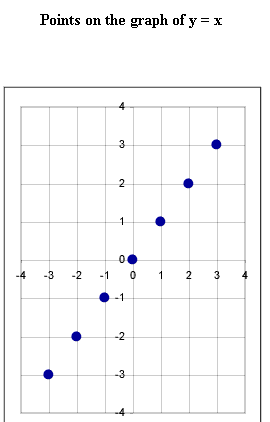
Basic Points of the Basic Linear Function y = x

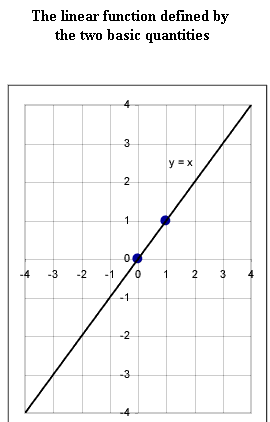
• The graph of y = x passes through the points indicated in the first graph, as you can easily verify by making  table.
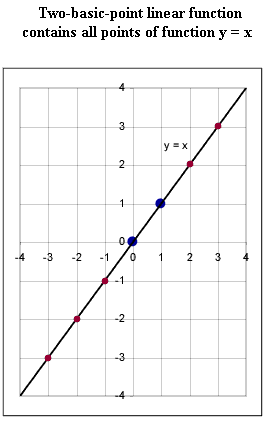
• The two basic points, which are the x = 0 and x = 1 points, are shown in the second figure.

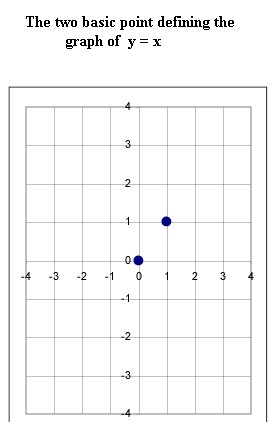
• The graph of y = x is defined by these two basic points as the straight line passing through the points.
• Note in the second figure that this line contains all the points shown in the original graph.

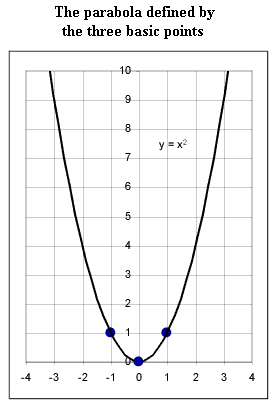
Basic Points of the Basic Quadratic Function y = x^2

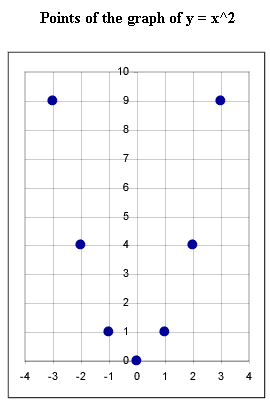
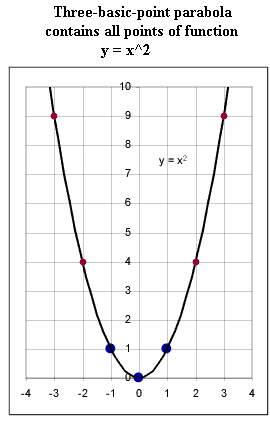
• The graph of y = x^2 passes through the points indicated in the first graph, as you can easily verify by making  table.
• The three basic points, which are the x = 0, x = 1 and x = -1 points, are shown in the second figure.

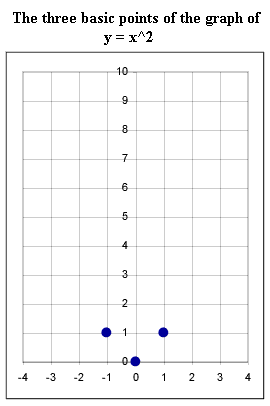
• The graph of y = x^2 is defined by these three basic points as the parabola passing through the points.  A parabola is a very specific type of shape, not just anything which appears sort of U-shaped.  Every parabola can be defined in terms of a quadratic function.  If it can't be defined in terms of a quadratic function it's not a parabola.
• Note in the second figure that this parabola contains all the points shown in the original graph.

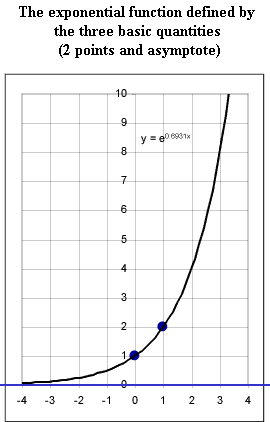
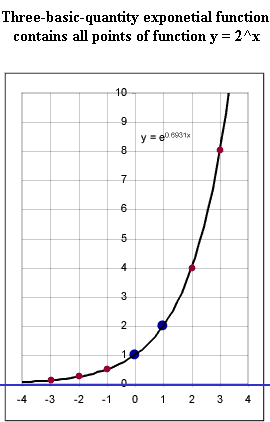
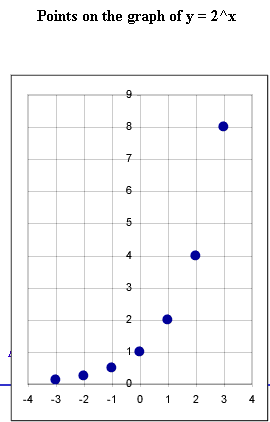
Basic Quantities (two points and asymptote) of the Basic Exponential Function y = 2^x

• The graph of y = 2^x passes through the points indicated in the first graph, as you can easily verify by making  table.
• The two basic points and the horizontal asymptote, which are the x = 0 and x = 1 points and the x axis (y = 0), are shown in the second figure.

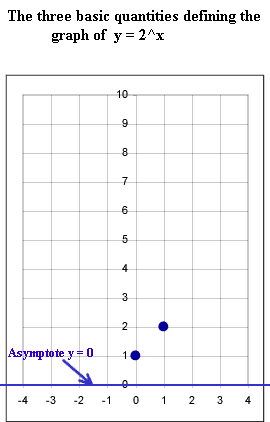
• The graph of y = 2^x  is defined by these two basic points and the asymptote.  This graph doesn't have a specific name; it's just referred to as the graph of an exponential function.
• Note in the second figure that the function as shown contains all the points shown in the original graph.