When two functions f(x) and g(x) are multiplied we get the function y = f(x) * g(x), which is written y = fg(x).
Suppose for example that an individual experiences seasonal mood swings, represented by the sine curve of the graph below (the straight line will be explained in the next paragraph):
Suppose furthermore that the strength of the mood swings is increasing yearly, as indicated by the linear function of the graph.
The scale of the graph is such that the values of the sine function fluctuate from -1 to 1 on a yearly cycle.
Note: The function f(x) = sin(2`pi x) has been constructed through a process you will encounter in the second semester of this course to complete exactly one cycle every year. The graph therefore represents approximately 6 years. You don't need to understand how the sine function was used, or even how it is defined. You should, however, understand that it can be evaluated on your calculator or using DERIVE, and that if evaluated on a calculator you must use radian mode.
It is fairly easy to understand that the mood vs. time graph might be something like the graph shown below:
This graph shows the mood vs. time function as a heavy (blue) line, with the basic seasonal function (the sine function) and the linear function by which seasonal fluctuations increase as light (black) lines. The dotted straight black line shows the negative of the straight black graph.
This blue graph was obtained by multiplying the values of the sine function by the values of the linear function g(x) = x + .3. The graph of this 'blue' function is therefore the graph of
'blue' function: gf(x) = g(x) * f(x) = (x + .3) * sin(2`pi x).
When the sine function f(x) is 0, the product of the two functions is 0. This happens 13 times on the graph. You should identify the points where this occurs, and note that both functions are zero at those points.
When the sine function reaches its 'peaks', where it takes a maximum value of 1, the product function must be
sine peak value = f(x)*g(x) = (x + .3) sin(2`pi x) = (x + .3) * 1 = x + .3,
which is just the value of the g(x) = x + .3 function. So at these peaks of the sine function, the product function will be equal to the linear g(x) function, and the graph of the product g(x) f(x) will for an instant lie on the graph of the linear function. At these points the graph of the product function touches the graph of the linear function.
When the sine function reaches its 'valleys', where it takes its minimum value -1, the product function is
sine 'valley' value = f(x)*g(x) = (x + .3) sin(2`pi x) = (x + .3) * -1 = -(x + .3),
which is just the value of the dotted-line function. At these points the graph of the product function touches the graph of the dotted-line function.
From this example you can see the following characteristics of graphs of the product function fg(x):
Exercises 1-6When either f(x) or g(x) is 0, then the product function also has a 0 for that value of x.
*When the magnitude | f(x) | of f(x) is greater than 1 (i.e., when the graph of f(x) is more than one unit from the x axis), then the product function will be further from the x axis than the g(x) function.
*When the magnitude | f(x) | of f(x) is less than 1 (i.e., when the graph of f(x) is less than one unit from the x axis), then the product function will be closer to the x axis than the g(x) function.
When f(x) and g(x) are either both positive or both negative, the product function is positive. When f(x) and g(x) have opposite signs the product function is negative.
*When f(x) = 1, the graph of the product function coincides with the graph of g(x).
The statements marked with asterisks (*) are symmetric in the sense that another true statement will be obtained if the labels f(x) and g(x) are interchanged throughout the statement.
1. Explain in terms of the example of this section the meaning of each of the above statements about graphs of product functions. Accompany your explanations with sketches and graphs clearly indicating the reasons for the characteristics.
2. The table given below shows values of y = f(x) = sin(2`pi x) and of y = g(x) = x + .3. Fill in the column for y = g(x) * f(x) = (x + .3) sin(2`pi x).
x |
f(x) = sin(2`pi x ) |
g(x) = (x+.3) | g(x)*
f(x) =
(x+.3) sin(2`pi x) |
0 |
0 |
0.3 |
|
0.25 |
1 |
0.55 |
|
0.5 |
0 |
0.8 |
|
0.75 |
-1 |
1.05 |
|
1 |
0 |
1.3 |
|
1.25 |
1 | 1.55 |
|
1.5 |
0 |
1.8 |
|
1.75 |
-1 | 2.05 |
|
2 |
0 |
2.3 |
|
2.25 |
1 | 2.55 |
|
2.5 |
0 |
2.8 |
|
2.75 |
-1 | 3.05 |
|
3 |
0 |
3.3 |
|
3.25 |
1 | 3.55 |
|
3.5 |
0 |
3.8 |
Sketch your own graph of the product function and verify that it has the same shape as that given on the graph above.
3. The table below shows values of y = f(x) = sin(2`pi x). Fill in values for the exponential function y = g(x) = -(e ^ (-.5 x) ) + 2, then determine the values of the product function y = g(x) * f(x). Sketch a graph of the product function. Finally, interpret this graph in terms of a mood function at the onset of a mental illness whose intensity asymptotically approaches an asymptotic limit.
x |
f(x) = sin(2`pi x ) |
g(x) =
-(e^(-.5 x) ) + 2 |
g(x)*
f(x) =
|
0 |
0 |
||
0.25 |
1 |
||
0.5 |
0 |
||
0.75 |
-1 |
||
1 |
0 |
||
1.25 |
1 | ||
1.5 |
0 |
||
1.75 |
-1 | ||
2 |
0 |
||
2.25 |
1 | ||
2.5 |
0 |
||
2.75 |
-1 | ||
3 |
0 |
||
3.25 |
1 | ||
3.5 |
0 |
4. Sketch graphs for y = f(x) = 2^x and y = g(x) = .5 x, for -2 < x < 2. Use your graphs to predict the shape of the y = g(x) * f(x) graph.
Make a table and graph for y = f(x) = 2^x, y = g(x) = .5 x, and y = g(x) * f(x), using x values -2, -1.5, -1, ..., 2. Sketch the 'accurate' y = g(x) * f(x) = .5 x (2 ^ x) graph on your previous graph and compare your results with your predictions.
5. Sketch graphs for y = f(x) = 2^x, y = g(x) = x^2, for -2 < x < 2. Use your graphs to predict the shape of the y = g( x) * f(x) graph.
Make a table and graph for y = f(x) = 2^x, y = g(x) = x^2, and y = g(x) * f(x), using x values -2, -1.5, -1, ..., 2. Sketch the 'accurate' y = g(x) * f(x) = x^2 (2 ^ x) graph on your previous graph and compare your results with your predictions.
6. The function y = f(x) has a smooth continuous graph with the following characteristics:
f(x) > 1 when x < -2 and when x > 1
-1 <= f(x) <= 1 when -2 < x < 1
f(x) = 0 when x = -1, -.5, 0 and .5
the graph passes through the x axis at every zero (i.e., it never just touches the x axis in a parabolic manner)
The function y = g(x) also has a smooth continuous graph with the following characteristics:
g(x) has asymptotes at y = -2 and y = +2
the slope g(x) is always positive (i.e., the values of g(x) always increase as we move from left to right)
g(x) = 0 at x = 1
| g(x) | = 1 at x = -3 and at x = +3
Sketch graphs of f(x) and g(x) functions with these characteristics.
Identify and graph all the points of the product function fg(x) = f(x) * g(x) for which the following hold:
fg(x) = f(x)
f(x) = 0
fg(x) = 0
g(x) = 1
fg(x) = g(x)
f(x) = 1
Identify the intervals of the x axis where each of the following apply:
Composite functions|fg(x)| > |g(x)|
|fg(x)| < |g(x)|
|fg(x)| > |f(x)|
|fg(x)| < |f(x)|
fg(x) > 0
fg(x) < 0
The process of forming of composite function consists of applying two functions in turn. We apply the first function to our x values, then apply the second function to the resulting values.
We have already seen composite functions in the context of inverse functions. Recall that a pair of inverse functions has the property that if we start with a value x and apply the first function, then apply the second function to that value, we and up back at our original value x.
We can use the functions f(x) = sin(2`pi x) and g(x) = x + .3 to illustrate the process of forming a composite function when the functions are not inverses. Suppose that we wish to apply first the function g then the function f.
If we start with x = 2, for example, we will proceed as follows:
Starting with x = 2, we first apply g to obtain g(2) = 2 + .3= 2.3.
We will then apply f to the resulting value, 2.3, to obtain f(2.3) = sin(2`pi(2.3)).
We could abbreviate this process by writing 2 -> g(2)=2.3 -> f(2.3) = sin(2`pi(2.3)).
Note that the process could have been expressed more symbolically as follows:
Starting with x = 2, we first apply g to obtain g(2).
We will then apply f to the resulting value, g(2), to obtain f(g(2)).
We could abbreviate this process by writing 2 -> g(2) -> f( g(2) ).
Had we started with x = q, we would have obtained the value g(q) from the first function; then application of f would yield f( g(q) ).
We could symbolize this process as q -> g(q) -> f(g(q)).
In general we symbolize the process as x -> g(x) -> f(g(x)).
Of course the expression f(g(x)) could be written, substituting x + .3 for g(x), as
f(g(x)) = f(x + .3).
Since f(x) = sin(2`pi x), the expression f(x + .3) could then be written as
f(g(x)) = f(x+.3) = sin(2`pi (x+.3)).
We note that the graph of y = f(x+.3) is just a shifted graph of y = f(x). The shift is -.3 units in the x direction.
The function f(g(x)) is called the composite of f with g.
A partial table for this function is shown below:
x |
(x+.3) |
sin(2`pi(x+.3)) |
0 |
0.3 |
0.951351 |
0.1 |
0.4 |
0.588816 |
0.2 |
0.5 |
0.001593 |
0.3 |
0.6 |
-0.58624 |
0.4 |
0.7 |
-0.95037 |
0.5 |
0.8 |
-0.95184 |
0.6 |
0.9 |
-0.5901 |
0.7 |
1 |
-0.00319 |
0.8 |
1.1 |
0.584947 |
0.9 |
1.2 |
0.949868 |
1 |
1.3 |
0.952328 |
1.1 |
1.4 |
0.591387 |
1.2 |
1.5 |
0.004778 |
1.3 |
1.6 |
-0.58365 |
1.4 |
1.7 |
-0.94937 |
1.5 |
1.8 |
-0.95281 |
The corresponding graph is depicted below, with the original function y = sin(2`pi x) depicted by a light (black) line and the composite by the heavy (red) line.
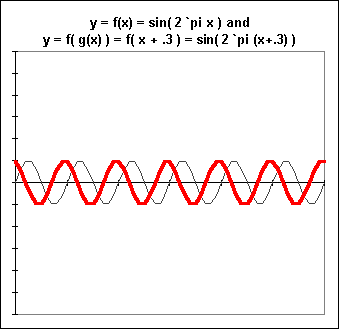
Compare this graph of y = f(g(x)) with the graph of fg(x). You will see that they are very different. The process of forming a composite function from two functions is very different from the process of forming the product of two functions, even though the notations f(g(x)) and fg(x) look very similar. In one process the values of two functions are being multiplied, whereas in the other the value of one function is acted upon, not multiplied, by the other.
Make note of the fact that this particular composite cause a horizontal shift in the graph of the f(x) function. This does not happen in general. It only happened because g(x) = x + .3 gave us a composite of the form f(x+.3), which constitutes a horizontal shift. If g(x) had been 4x^2 + 2x - .3, for example, the composite would have been f(4 x^2 + 2x -.3), which does not constitute a horizontal shift.
Examples of the occurrence of composite functionsComposite functions arise naturally in nearly every area where mathematical modeling is important.
Example 1: Range of flow is a function of water depth which is a function of time
Recall our original experiment with water flowing from a uniform cylinder. We noted that the depth of the water was a quadratic function of time. We also noted that the horizontal range of the flow was a linear function of time.
The reason for this connection can be understood by realizing that the horizontal range of flow is in fact a composite function of time. It turns out that the range of flow for the system we observed is a function of depth, which as stated is a quadratic function of time. So if we know the time, we can find the depth and knowing the depth we find the horizontal range of flow. Our procedure can be symbolized by
t -> depth(t) -> range(depth(t)),
which is simply the procedure for finding the composite of the range and depth functions.
As a specific example, suppose that the depth function is
depth(t) = (.2 t - 10)^2.
We see that this function has a repeated zero at t = 50, since .2t - 10 = 0 when t = 50.
It turns out that for the system we observed, horizontal range is given as a function of depth by the approximate power function
range ( depth ) = 1.3 `sqrt(depth).
This is a power function with power p = .5, corresponding to the square root (remember that `sqrt(a) = a^.5).
Now, noting that clock time t gives us depth which in turn gives us range, we can calculate the range at any depth.
For example if t = 10,
depth(t) = (.2 * 10 - 10) ^2 = 64
range(depth) = 1.3 `sqrt(depth) = 1.3 `sqrt(64) = 10.4.
In general, for a given time t, we have
depth(t) = (.2 t = 10) ^ 2 , so
range(depth(t)) = range((.2t - 10) ^ 2))
= 1.3 * `sqrt( (.2t - 10) ^ 2)
= 1.3(.2t - 10)
= 2.6t - 13
Thus range turns out to be a function of time t:
range(t) = range(depth(t)) = 2.6 t - 26.
Note that range(t) is thus a linear function of time.
Example 2: Engine power is a function of speed which is a function of time
The power needed from an ocean liner's engines as it accelerates uniformly away from the dock increases with the ship's speed, since the faster the ship travels the more resistance it feels from the water, and the more water it has to plow through.
If the number of horsepower required of the engine is given as a function of the ship's velocity by
power(v) = 7000 v^3 + 3000,
and if the ship's velocity is given as a function of time t in minutes by
v(t) = .3 t + 1,
then the power is obtained from a sequence of calculations
t -> v(t) -> power( v(t) ).
For example if t = 4, then
t=4
-> v(t) = .3(4) + 1 = 2.2
-> power( v(t) ) = power (2.2 ) = 7000 * 2.2^3 + 3000 = 71500 (approx.)
More generally, we obtain
power (v(t) ) = power (.3t + 1) = 7000 (.3 t + 1) ^ 3 + 3000.
This expression can be simplified to yield
7000 (.027 t^3 + .27 t^2 + .9 t + 1) + 3000 = 169 t^3 + 1890 t^2 + 6300 t + 10000.
So the final expression is
power(t) = 169 t^3 + 1890 t^2 + 6300 t + 10000.
If this expression is evaluated at t = 4 (recall that we obtained power of approximate 71500 for t = 4), we obtain
power(t) = 169 * 4^3 + 1890 * 4^2 + 6300 * 4 + 10000 = 71500,
in agreement with our previous result.
Exercises 7-107. For a certain container, range(depth) = 2.9 `sqrt(depth) and depth(t) = t^2 - 40 t + 400.
Determine the times when depth is 0 and show that the vertex of the graph of depth vs. time coincides with these zeros.
Express the depth function as a product of linear factors.
For t = 5, 10 and 15, determine the depth and from the depth determine the range.
Find the general form of the composite range(depth(t)), and simplify this form to show that it is a linear function of time.
Use the general form of the composite to determine depth at times t = 5, 10 and 15.
8. At distance r from a certain light source, the illumination in Watts/square meter is
Illumination(r) = 40 / r^2.
An individual is calmly rolling down a gentle incline in a runaway wagon, calculating her speed by the rate at which the brightness of the light changes. If the distance of the wagon from the source is given as a function of time by
distance = 400 - .04 t^2,
find the composite function illumination(distance(t)).
Use this function to determine the illumination at t = 25, t = 50 and t = 75.
At what average rate is illumination changing during the time interval from t = 25 to t = 50, and from t = 50 to t = 75?
9. If the daily cost of heating or cooling a house when outside temperature is T is given by the function
cost(Temp) = $(.35 + .03 `sqrt( (75 - Temp)^2 ) ),
and if the average daily temperature is given as a function of the number t of days since Jan 1 as
Temp(t) = 50 + 30 sin( 2`pi ( t - 80)/365 ),
then what is the average daily cost on days t = 0, 90, 180 and 270?
What is the composite function cost( Temp(t) ) ?
Evaluate your composite function at t = 0, 90, 180 and 270 to check your expression.
10. For a certain individual, the expected grade average is a function of the number of weekly hours t spent in concentrated study according to the function
gradeAverage = -.5 + t / 10.
The number of hours spent is a function t(Q) of the individuals mental health quotient Q, a hypothetical measure related to hours spent by the relation
t(Q) = 50 (1 - e ^ (-.02 (Q - 70) ) ).
If the student's mental health quotient is an average 100, then what grade average should the student expect?
What grade averages would be expected for mental health quotients of 110, 120 and 130?
What is the upper limit on the expected grade average that can be achieved by this student?
What is the composite function gradeAverage( t(Q) )?
Evaluate your composite function at t = 100, 110, 120 and 130 to check your work.